前篇:
云课五分钟-0ALinux文件系统及权限-查询命令如何使用
智能大模型个人感觉完全颠覆式改变了学习和教学的模式,知识的重要性荡然无存。
越来越需要重视思路和方法,创新和创意。
09+0A:接着如下
Linux基础入门的内容包括以下几个方面:
- Linux基础命令:学习如何在Linux终端中使用基础命令,如文件和目录操作、进程管理、文本编辑等。这些命令是你在Linux中进行日常操作的基础。
- Linux文件系统及权限:理解Linux的文件系统结构以及如何设置和更改文件和目录的权限,这对于管理Linux系统非常重要。
- Linux软件包管理:学习如何使用Linux的软件包管理系统,如apt、yum等,安装、更新和卸载软件包。
- Linux用户及组管理:理解Linux中的用户和组概念,学习如何创建、删除和管理用户及组。
- Linux服务器基础:初步了解Linux服务器的基本配置和管理,例如SSH远程登录、防火墙配置等。
- vi/vim编辑器:学习使用vi或vim文本编辑器,它是Linux系统下最常用的文本编辑器之一。
- Shell脚本编程基础:学习Shell脚本编程,能够编写简单的脚本,提高自动化处理任务的能力。
以上就是Linux基础入门的主要内容。这些内容能够帮助你建立起对Linux系统的基本理解,并掌握基本的操作技能。
1+2对应09+0A,同样方式继续3/4/5/6/7,没有必要再继续录制视频,同类的知识也是如此。
视频:
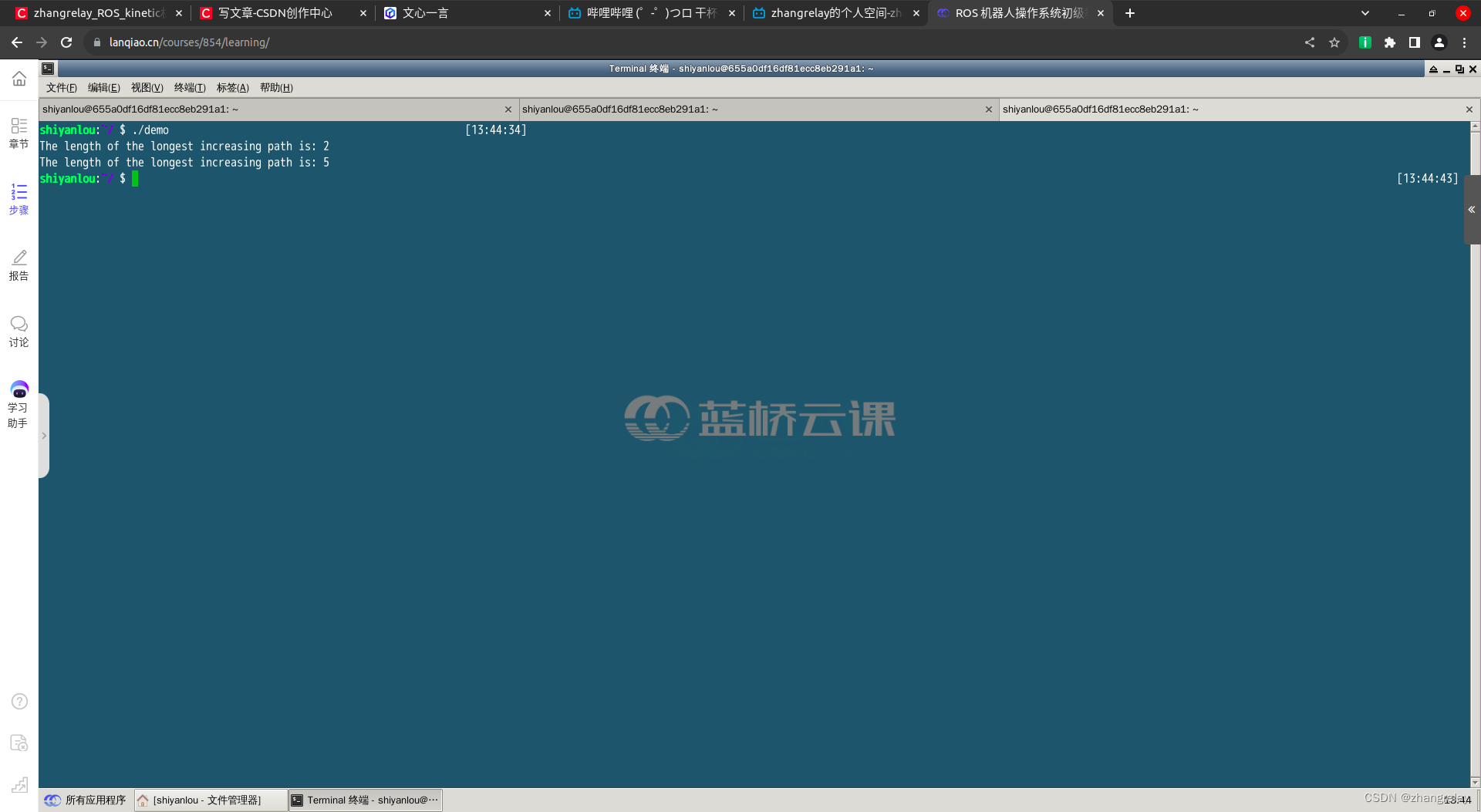
云课五分钟-0B快速排序C++示例代码-注释和编译指令参数-std=c++11
文本:
刷Leetcode???
#include <vector>
#include <algorithm>
using namespace std;
class Solution {
public:
int longestIncreasingPath(vector<vector<int>>& matrix) {
if (matrix.empty()) return 0;
int m = matrix.size();
int n = matrix[0].size();
vector<vector<int>> cache(m, vector<int>(n, 0)); // 记录每个点的最长路径长度
int result = 1;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
result = max(result, dfs(matrix, i, j, cache));
}
}
return result;
}
private:
int dfs(vector<vector<int>>& matrix, int i, int j, vector<vector<int>>& cache) {
if (cache[i][j] != 0) return cache[i][j]; // 如果已经计算过,则直接返回结果
int m = matrix.size();
int n = matrix[0].size();
int result = 1;
// 向南和向东进行深度优先搜索
if (i + 1 < m && matrix[i + 1][j] > matrix[i][j]) {
result = max(result, dfs(matrix, i + 1, j, cache) + 1);
}
if (j + 1 < n && matrix[i][j + 1] > matrix[i][j]) {
result = max(result, dfs(matrix, i, j + 1, cache) + 1);
}
cache[i][j] = result; // 记录当前点的最长路径长度
return result;
}
};
int main() {
Solution solution;
vector<vector<int>> matrix = {{9, 9, 4}, {6, 6, 8}, {2, 1, 1}};
int result = solution.longestIncreasingPath(matrix);
cout << "The length of the longest increasing path is: " << result << endl;
return 0;
}学习LeetCode C++,可以从以下几个步骤进行:
- 基础语法学习:首先,你需要对C++的基础语法有深入的理解,包括数据类型,变量,函数,控制流,指针,面向对象编程等。在这个阶段,你可以通过读书,看在线课程等方式进行学习。
- 编程技巧学习:在掌握了基础语法之后,你需要学习一些C++的编程技巧,比如如何使用STL(标准模板库),如何进行内存管理等。这些技巧将帮助你更好地解决算法问题。
- 算法和数据结构学习:在LeetCode中,算法和数据结构是核心。你需要对常见的算法和数据结构有深入的理解,比如数组,链表,栈,队列,哈希表,二叉树,图等。你不仅需要知道这些数据结构的基本操作,还需要知道如何在实际问题中应用它们。
- 刷题:在有了以上的基础之后,你就可以开始在LeetCode上刷题了。可以先从简单的问题开始,逐步提升难度。在刷题的过程中,你需要注意的是,不仅要写出正确的答案,还需要优化你的代码,使其运行时间最短,使用的内存最少。
- 总结和反思:刷题并不是越多越好,你需要经常总结和反思。看看哪些问题你经常出错,哪些问题你解决不了,然后有针对性地进行改进。
- 交流和分享:加入一些学习群或者社区,和其他人交流学习经验,分享解题技巧,也能帮助你提升水平。
记住,编程是一项需要不断实践和学习的技能,只有持之以恒地努力,才能不断提升自己的水平。祝你在LeetCode的学习中取得好成绩!
其实智能大模型几乎不可能输给人类,如同围棋等……
当然,以下是一个来自LeetCode的简单案例:题目 "两数之和"(题目编号:1)的C++解法。
题目描述:
给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那两个整数,并返回他们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素不能使用两遍。
示例:
给定 nums = [2, 7, 11, 15], target = 9
因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]
C++解法:
#include <vector>
#include <unordered_map>
using namespace std;
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int, int> mp;
vector<int> result;
for(int i = 0; i < nums.size(); ++i){
int complement = target - nums[i];
if(mp.find(complement) != mp.end()){
result.push_back(mp[complement]);
result.push_back(i);
return result;
}
mp[nums[i]] = i;
}
return result;
}
};cpp
#include <vector> | |
#include <unordered_map> | |
using namespace std; | |
class Solution { | |
public: | |
vector<int> twoSum(vector<int>& nums, int target) { | |
unordered_map<int, int> mp; | |
vector<int> result; | |
for(int i = 0; i < nums.size(); ++i){ | |
int complement = target - nums[i]; | |
if(mp.find(complement) != mp.end()){ | |
result.push_back(mp[complement]); | |
result.push_back(i); | |
return result; | |
} | |
mp[nums[i]] = i; | |
} | |
return result; | |
} | |
}; |
这个解法利用哈希表存储数组中的元素及其索引,通过查找目标值与当前元素的差值,如果存在这个差值,则说明找到了目标值的两个数,返回它们的索引。注意,这个解法中返回的结果是按照题目要求的顺序,即较小的索引在前,较大的索引在后。
当然,以下是一个来自LeetCode的困难案例:题目 "正则表达式匹配"(题目编号:10)的C++解法。
题目描述:
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '' 的正则表达式匹配。'.' 匹配任意单个字符。'' 匹配零个或多个前面的那一个元素。
示例:
- 输入: s = "aa", p = "a" 输出: false
- 输入: s = "aa", p = "a*" 输出: true
- 输入: s = "ab", p = ".*" 输出: true
- 输入: s = "aab", p = "cab" 输出: true
C++解法:
#include <vector>
using namespace std;
class Solution {
public:
bool isMatch(string s, string p) {
int m = s.size();
int n = p.size();
vector<vector<bool>> dp(m + 1, vector<bool>(n + 1, false));
dp[0][0] = true;
for (int j = 1; j <= n; ++j) {
if (p[j - 1] == '*') {
dp[0][j] = dp[0][j - 2];
}
}
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
if (s[i - 1] == p[j - 1] || p[j - 1] == '.') {
dp[i][j] = dp[i - 1][j - 1];
} else if (p[j - 1] == '*') {
dp[i][j] = dp[i][j - 2];
if (p[j - 2] == '.' || p[j - 2] == s[i - 1]) {
dp[i][j] = dp[i][j] || dp[i - 1][j];
}
} else {
dp[i][j] = false;
}
}
}
return dp[m][n];
}
};cpp
#include <vector> | |
using namespace std; | |
class Solution { | |
public: | |
bool isMatch(string s, string p) { | |
int m = s.size(); | |
int n = p.size(); | |
vector<vector<bool>> dp(m + 1, vector<bool>(n + 1, false)); | |
dp[0][0] = true; | |
for (int j = 1; j <= n; ++j) { | |
if (p[j - 1] == '*') { | |
dp[0][j] = dp[0][j - 2]; | |
} | |
} | |
for (int i = 1; i <= m; ++i) { | |
for (int j = 1; j <= n; ++j) { | |
if (s[i - 1] == p[j - 1] || p[j - 1] == '.') { | |
dp[i][j] = dp[i - 1][j - 1]; | |
} else if (p[j - 1] == '*') { | |
dp[i][j] = dp[i][j - 2]; | |
if (p[j - 2] == '.' || p[j - 2] == s[i - 1]) { | |
dp[i][j] = dp[i][j] || dp[i - 1][j]; | |
} | |
} else { | |
dp[i][j] = false; | |
} | |
} | |
} | |
return dp[m][n]; | |
} | |
}; |
这是一个典型的动态规划问题。我们使用二维数组 dp 来记录匹配状态,其中 dp[i][j] 表示字符串 s 的前 i 个字符与模式 p 的前 j 个字符是否匹配。通过逐个填充 dp 数组,我们可以得到最终的匹配结果。在填充过程中,我们根据当前字符的匹配情况和模式的特殊字符(. 和 *)进行相应的逻辑处理。最后返回 dp[m][n],即整个字符串和模式是否匹配的结果。
当然,以下是一个来自LeetCode的顶级难度案例:题目 "最长递增路径"(题目编号:329)的C++解法。
题目描述:
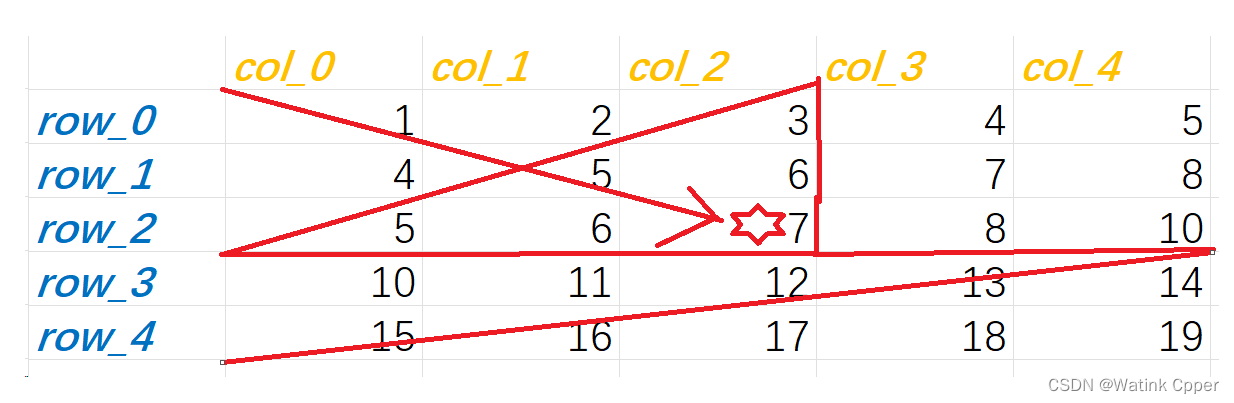
给定一个包含非负整数的 m x n 网格,请找出其中最长递增路径的长度。
对于每个网格单元,你可以移动到南边或东边的相邻单元(如果存在)。南方向的移动可以视为 (row, col) 到 (row + 1, col) 的移动,而东方向的移动可以视为 (row, col) 到 (row, col + 1) 的移动。
你不能向北或向西移动,同时不允许重复访问网格中的单元。
示例:
输入:
[9,9,4],
[6,6,8],
[2,1,1]
输出: 4
解释: 最长递增路径为 1→ 2→ 9→ 6→ 9。
C++解法:
#include <vector>
#include <algorithm>
using namespace std;
class Solution {
public:
int longestIncreasingPath(vector<vector<int>>& matrix) {
if (matrix.empty()) return 0;
int m = matrix.size();
int n = matrix[0].size();
vector<vector<int>> cache(m, vector<int>(n, 0)); // 记录每个点的最长路径长度
int result = 1;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
result = max(result, dfs(matrix, i, j, cache));
}
}
return result;
}
private:
int dfs(vector<vector<int>>& matrix, int i, int j, vector<vector<int>>& cache) {
if (cache[i][j] != 0) return cache[i][j]; // 如果已经计算过,则直接返回结果
int m = matrix.size();
int n = matrix[0].size();
int result = 1;
// 向南和向东进行深度优先搜索
if (i + 1 < m && matrix[i + 1][j] > matrix[i][j]) {
result = max(result, dfs(matrix, i + 1, j, cache) + 1);
}
if (j + 1 < n && matrix[i][j + 1] > matrix[i][j]) {
result = max(result, dfs(matrix, i, j + 1, cache) + 1);
}
cache[i][j] = result; // 记录当前点的最长路径长度
return result;
}
};cpp
#include <vector> | |
#include <algorithm> | |
using namespace std; | |
class Solution { | |
public: | |
int longestIncreasingPath(vector<vector<int>>& matrix) { | |
if (matrix.empty()) return 0; | |
int m = matrix.size(); | |
int n = matrix[0].size(); | |
vector<vector<int>> cache(m, vector<int>(n, 0)); // 记录每个点的最长路径长度 | |
int result = 1; | |
for (int i = 0; i < m; ++i) { | |
for (int j = 0; j < n; ++j) { | |
result = max(result, dfs(matrix, i, j, cache)); | |
} | |
} | |
return result; | |
} | |
private: | |
int dfs(vector<vector<int>>& matrix, int i, int j, vector<vector<int>>& cache) { | |
if (cache[i][j] != 0) return cache[i][j]; // 如果已经计算过,则直接返回结果 | |
int m = matrix.size(); | |
int n = matrix[0].size(); | |
int result = 1; | |
// 向南和向东进行深度优先搜索 | |
if (i + 1 < m && matrix[i + 1][j] > matrix[i][j]) { | |
result = max(result, dfs(matrix, i + 1, j, cache) + 1); | |
} | |
if (j + 1 < n && matrix[i][j + 1] > matrix[i][j]) { | |
result = max(result, dfs(matrix, i, j + 1, cache) + 1); | |
} | |
cache[i][j] = result; // 记录当前点的最长路径长度 | |
return result; | |
} | |
}; |
这是一个经典的深度优先搜索(DFS)问题,同时利用动态规划的思想进行记忆化搜索,避免了重复计算。通过遍历每个网格单元,并对其进行DFS搜索,找到以当前网格单元为起点的最长递增路径。使用一个缓存数组 cache 来记录每个网格单元对应的最长路径长度,避免重复计算。最终遍历整个网格后,找到最长路径的长度,即为结果。
您提供的代码是一个在二维矩阵中寻找最长递增路径的长度的问题。看起来您在末尾标注了(linux -std=C++11),可能是想询问如何在Linux环境下使用C++11标准编译和运行这段代码。
首先,这段代码本身看起来没有逻辑问题,它是基于深度优先搜索的思想来解决的。
现在,关于如何在Linux环境下使用C++11标准来编译和运行这段代码,你可以遵循以下步骤:
-
保存代码:将您的代码保存为一个
.cpp文件,例如solution.cpp。 -
编写主函数:您提供的代码是一个类,所以您需要在一个主函数中创建一个该类的实例,并调用其方法。例如:
int main() {
Solution solution;
vector<vector<int>> matrix = {{9, 9, 4}, {6, 6, 8}, {2, 1, 1}};
int result = solution.longestIncreasingPath(matrix);
cout << "The length of the longest increasing path is: " << result << endl;
return 0;
}cpp复制代码
int main() { | |
Solution solution; | |
vector<vector<int>> matrix = {{9, 9, 4}, {6, 6, 8}, {2, 1, 1}}; | |
int result = solution.longestIncreasingPath(matrix); | |
cout << "The length of the longest increasing path is: " << result << endl; | |
return 0; | |
} |
-
编译代码:在Linux终端中,使用
g++编译器,指定C++11标准进行编译:
bash复制代码
g++ -std=c++11 -o solution solution.cpp |
-std=c++11告诉编译器使用C++11标准,-o solution表示输出的可执行文件名为solution`。
4. 运行程序:编译成功后,运行生成的可执行文件:
bash复制代码
./solution |
如果一切顺利,您应该会看到终端输出最长递增路径的长度。
以下是一个使用C++实现的快速排序示例代码:
cpp复制代码
#include <iostream> | |
#include <vector> | |
using namespace std; | |
int partition(vector<int>& arr, int low, int high) { | |
int pivot = arr[high]; | |
int i = low - 1; | |
for (int j = low; j <= high - 1; j++) { | |
if (arr[j] < pivot) { | |
i++; | |
swap(arr[i], arr[j]); | |
} | |
} | |
swap(arr[i + 1], arr[high]); | |
return i + 1; | |
} | |
void quickSort(vector<int>& arr, int low, int high) { | |
if (low < high) { | |
int pi = partition(arr, low, high); | |
quickSort(arr, low, pi - 1); | |
quickSort(arr, pi + 1, high); | |
} | |
} | |
int main() { | |
vector<int> arr = {10, 7, 8, 9, 1, 5}; | |
int n = arr.size(); | |
quickSort(arr, 0, n - 1); | |
for (auto i : arr) { | |
cout << i << " "; | |
} | |
return 0; | |
} |
这个示例程序使用了vector作为输入数据,通过实现partition函数和quickSort函数来完成快速排序的操作。其中,partition函数用来确定基准元素的位置,quickSort函数用来递归地对左右子序列进行排序。最终,程序输出排好序的数组。
以下是对您提供的代码的逐行注释:
cpp复制代码
// 引入输入输出流库,用于输入输出操作 | |
#include <iostream> | |
// 引入向量库,用于处理动态数组 | |
#include <vector> | |
// 使用标准命名空间,避免在调用标准库函数时前缀"std::" | |
using namespace std; | |
// 定义划分函数,用于在快速排序中划分数组 | |
int partition(vector<int>& arr, int low, int high) { | |
// 选取最后一个元素作为枢轴 | |
int pivot = arr[high]; | |
// 初始化指向较小元素的指针 | |
int i = low - 1; | |
// 遍历数组,对元素进行比较 | |
for (int j = low; j <= high - 1; j++) { | |
// 若当前元素小于枢轴,则交换当前元素与指向较小元素的指针所指向的元素 | |
if (arr[j] < pivot) { | |
i++; | |
swap(arr[i], arr[j]); | |
} | |
} | |
// 将枢轴元素与指向较小元素的指针后一位进行交换,这样就将数组划分为两部分 | |
swap(arr[i + 1], arr[high]); | |
// 返回划分点的位置 | |
return i + 1; | |
} | |
// 定义快速排序函数 | |
void quickSort(vector<int>& arr, int low, int high) { | |
// 若当前划分区间不为空,则进行排序 | |
if (low < high) { | |
// 获取划分点位置 | |
int pi = partition(arr, low, high); | |
// 对划分点左边部分进行递归排序 | |
quickSort(arr, low, pi - 1); | |
// 对划分点右边部分进行递归排序 | |
quickSort(arr, pi + 1, high); | |
} | |
} | |
// 主函数,程序入口点 | |
int main() { | |
// 定义一个待排序的数组 | |
vector<int> arr = {10, 7, 8, 9, 1, 5}; | |
// 获取数组长度 | |
int n = arr.size(); | |
// 对数组进行快速排序 | |
quickSort(arr, 0, n - 1); | |
// 打印排序后的数组元素 | |
for (auto i : arr) { | |
cout << i << " "; | |
} | |
return 0; | |
} |
以上注释基本上解释了代码中的每个部分以及它们是如何在快速排序算法中工作的。
下面是一个符合C++98规范的快速排序示例代码:
cpp复制代码
#include <iostream> | |
#include <vector> | |
#include <algorithm> | |
using namespace std; | |
int partition(vector<int>& arr, int low, int high) { | |
int pivot = arr[high]; | |
int i = low - 1; | |
for (int j = low; j < high; j++) { | |
if (arr[j] <= pivot) { | |
i++; | |
swap(arr[i], arr[j]); | |
} | |
} | |
swap(arr[i + 1], arr[high]); | |
return i + 1; | |
} | |
void quickSort(vector<int>& arr, int low, int high) { | |
if (low < high) { | |
int pi = partition(arr, low, high); | |
quickSort(arr, low, pi - 1); | |
quickSort(arr, pi + 1, high); | |
} | |
} | |
int main() { | |
vector<int> arr = {10, 7, 8, 9, 1, 5}; | |
int n = arr.size(); | |
quickSort(arr, 0, n - 1); | |
for_each(arr.begin(), arr.end(), [](int num) { | |
cout << num << " "; | |
}); | |
cout << endl; | |
return 0; | |
} |
这个示例代码与之前的版本基本相同,但在以下几个方面进行了调整以符合C++98规范:
- 使用
#include <algorithm>头文件引入swap()函数。 - 使用
for_each()函数来遍历和打印数组元素,这是C++98中提供的一种遍历容器的方法。这里还使用了lambda表达式作为函数参数,以简化代码。 - 在
partition()函数的for循环中,将条件从j <= high - 1修改为j < high,这是因为在C++98中,推荐使用半开半闭区间[low, high)来表示范围。这样的修改不会影响算法的正确性。 using namespace std;语句被保留,以简化代码中的标准库函数和对象的引用。然而,需要注意的是,在实际开发中,过多地使用using namespace std;可能会导致命名冲突和不可预见的错误。因此,通常建议在大型项目中避免使用该语句,而是显式地使用std::前缀来引用标准库的内容。
你的问题主要涉及到C++的不同版本和一些初始化的问题。让我们逐个解决它们:
-
vector<int> arr = {10, 7, 8, 9, 1, 5};这行代码在C++98中是不被支持的,因为C++98并不支持列表初始化。你需要使用数组或者vector的push_back方法来初始化。你可以改为如下方式:
cpp复制代码
vector<int> arr; | |
arr.push_back(10); | |
arr.push_back(7); | |
arr.push_back(8); | |
arr.push_back(9); | |
arr.push_back(1); | |
arr.push_back(5); |
或者你也可以使用数组进行初始化:
cpp复制代码
int arr[] = {10, 7, 8, 9, 1, 5}; | |
vector<int> vec(arr, arr + sizeof(arr)/sizeof(arr[0])); |
lambda expressions only available with -std=c++11 or -std=gnu++11这个警告是因为你在C++98模式下使用了C++11才有的lambda表达式。如果你想使用lambda表达式,需要将你的编译器升级到C++11模式。你可以在编译指令中加上-std=c++11参数,例如g++ -std=c++11 qs.cpp。- 对于
for_each的问题,也是因为你在C++98模式下使用了C++11的lambda表达式,如果你升级到了C++11模式,这个问题应该就会解决。另外,需要注意的是,for_each在C++17后已被弃用,建议改用其他算法如for_loop或者transform等。
总的来说,你的代码没有任何逻辑错误,只是由于编译器版本和初始化方式导致的这些问题。按照上述方法修改,应该就可以正常运行了。
-std=c++11 是一个编译器选项,用于指定编译器使用 C++11 标准来编译代码。C++11 是一种 C++ 编程语言的版本,它引入了许多新特性和改进,包括 lambda 表达式、智能指针、范围 for 循环等。
当你在编译 C++ 代码时使用 -std=c++11 选项,你告诉编译器使用 C++11 标准来解析和编译你的代码。这样,你就可以在代码中使用 C++11 引入的新特性和语法。
例如,如果你使用 g++ 编译器,你可以在命令行中使用以下命令来编译你的代码:
复制代码
g++ -std=c++11 your_code.cpp -o your_program |
这将使用 C++11 标准来编译 your_code.cpp 文件,并将生成的可执行文件命名为 your_program。确保在使用 C++11 特性时在编译器中指定 -std=c++11 选项,以确保代码的正确解析和编译。
-std=c++11 是一个编译器选项,用于指定编译器使用 C++11 标准来编译代码。C++11 是一种 C++ 编程语言的版本,它引入了许多新特性和改进,包括 lambda 表达式、智能指针、范围 for 循环等。
当你在编译 C++ 代码时使用 -std=c++11 选项,你告诉编译器使用 C++11 标准来解析和编译你的代码。这样,你就可以在代码中使用 C++11 引入的新特性和语法。
例如,如果你使用 g++ 编译器,你可以在命令行中使用以下命令来编译你的代码:
复制代码
g++ -std=c++11 your_code.cpp -o your_program |
这将使用 C++11 标准来编译 your_code.cpp 文件,并将生成的可执行文件命名为 your_program。确保在使用 C++11 特性时在编译器中指定 -std=c++11 选项,以确保代码的正确解析和编译。
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
class Solution {
public:
int longestIncreasingPath(vector<vector<int>>& matrix) {
if (matrix.empty()) return 0;
int m = matrix.size();
int n = matrix[0].size();
vector<vector<int>> cache(m, vector<int>(n, 0)); // 记录每个点的最长路径长度
int result = 1;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
result = max(result, dfs(matrix, i, j, cache));
}
}
return result;
}
private:
int dfs(vector<vector<int>>& matrix, int i, int j, vector<vector<int>>& cache) {
if (cache[i][j] != 0) return cache[i][j]; // 如果已经计算过,则直接返回结果
int m = matrix.size();
int n = matrix[0].size();
int result = 1;
// 向南和向东进行深度优先搜索
if (i + 1 < m && matrix[i + 1][j] > matrix[i][j]) {
result = max(result, dfs(matrix, i + 1, j, cache) + 1);
}
if (j + 1 < n && matrix[i][j + 1] > matrix[i][j]) {
result = max(result, dfs(matrix, i, j + 1, cache) + 1);
}
cache[i][j] = result; // 记录当前点的最长路径长度
return result;
}
};
int main() {
Solution solution;
vector<vector<int>> matrix1 = {{9, 9, 4}, {6, 6, 8}, {2, 1, 1}};
int result1 = solution.longestIncreasingPath(matrix1);
cout << "The length of the longest increasing path is: " << result1 << endl;
vector<vector<int>> matrix2 = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
int result2 = solution.longestIncreasingPath(matrix2);
cout << "The length of the longest increasing path is: " << result2 << endl;
return 0;
}