基本概念

        距离分析是对观测量之间相似或不相似程度的一种测度，是计算一对观测量之间的广义距离。这些相似性或距离测度可以用于其他分析过程，例如因子分析、聚类分析或多维定标分析，有助于分析复杂的数据集。

统计原理

不相似性测度

• 对定距数据的不相似性（距离）测度可以使用的统计量有：欧几里得距离、平方欧氏距离、切比雪夫距离、Block距离、明可斯基距离等。
• 对定序数据，主要使用卡方不相似测度和斐方测度。
• 对二值（只有两种取值）数据变量之间的距离描述，使用欧氏距离、平方欧氏距离、尺寸差异、模式差异、方差、形或兰斯和威廉斯等距离统计量。

相似性测度

•  对于定距数据主要使用皮尔逊相关系数和夹角余弦距离;
• 对于二值数据的相似性测度主要包括简单匹配系数、Jaccard相似性指数、Hamann相似性测度等20余种。
• 其中的距离又分为个案（观测记录）之间的距离和变量之间的距离两种。

分析步骤

        距离分析中不存在假设检验问题，主要是通过SPSS自动计算变量或个案之间的相似性或不相似性距离，根据其计算距离值的大小来确定变量或个案之间的相似性或不相似性的强弱。

SPSS实现举例

        

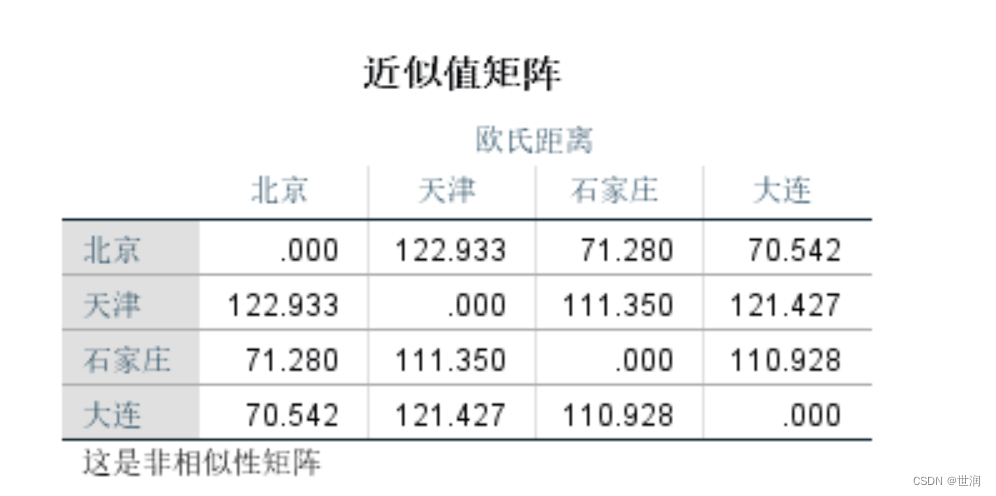
        表格的第一行（Euclidean 距离）说明采用的是欧氏距离。这是一个对称矩阵，当两变量的欧氏距离越大，说明其差别越大，反之越小。从表中可看出“北京”和“大连”的日照数最接近，而“北京”和“天津”的日照数相差最大。