一、概述

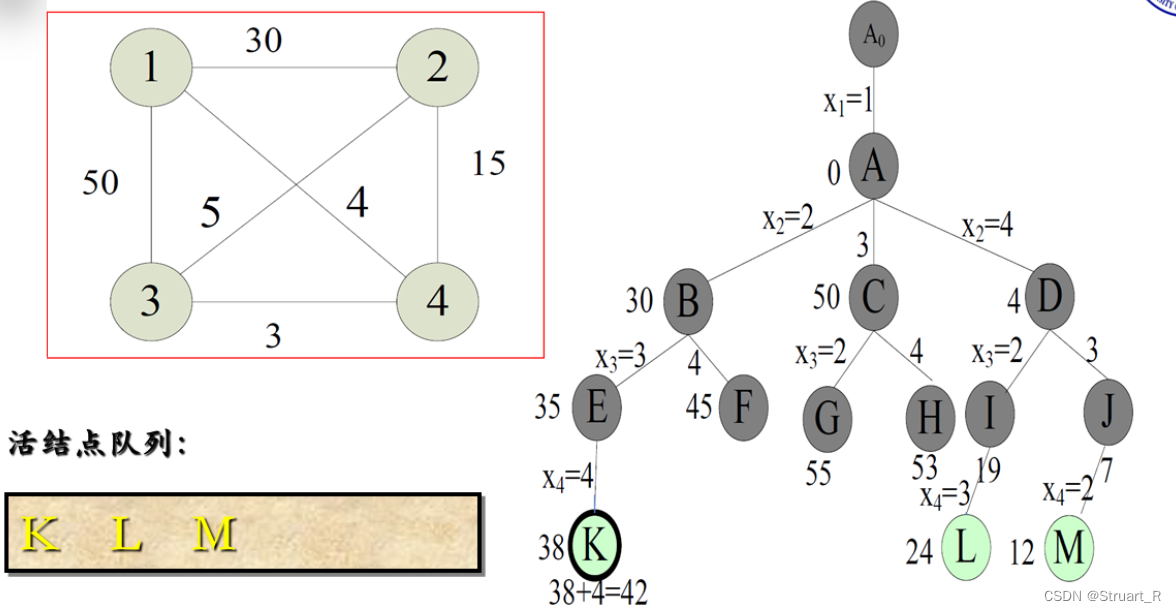
        有n个城市，旅行者要访问所有n个城市，最终回到起始点，假设起始点给定为1，城市间距离已知，求能够完成旅行的最短距离。题干如下图。

        算法：分支限界法，使用队列进行bfs搜索。

二、代码

import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
public class tsp {
    public static final int MAX=9999;
    public static int arr[][]={
        {MAX,MAX,MAX,MAX,MAX},
        {MAX,MAX,30,50,4},
        {MAX,30,MAX,5,15},
        {MAX,50,5,MAX,3},
        {MAX,4,15,3,MAX}
    };
    public static int size=arr.length;
    public static int costmin=MAX;
    public static int route[]=new int[arr.length];
    public static class traveling
    {
        public int cc;  //当前费用
        public int x[]=new int [size-1];     //当前路径
        public int n;   //当前连接点个数
        public int flag[]=new int[size];
        public traveling(int cc,int x[],int n,int flag[])
        {
            this.cc=cc;
            this.n=n;
            for(int i=0;i<n;i++)
            {
                this.x[i]=x[i];
            }
            for(int i=0;i<arr.length;i++)
            {
                this.flag[i]=flag[i];
            }
        }
    }
    public static void main(String[] args)
    {
        bfs();
        for(int i:route)
            System.out.print(i+" ");
        System.out.println();
        System.out.println("costmin:"+costmin);
    } 
    public static void bfs()
    {
        Queue<traveling>q=new LinkedList<>();
        int flag[]={0,1,0,0,0};
        int x[]={1};
        traveling tr=new traveling(0, x, 1,flag);
        q.offer(tr);
        while(!q.isEmpty())
        {
            tr=q.poll();
            int end=tr.x[tr.n-1]; //end队列中最后一个值
            int cc=tr.cc;
            if(tr.n==size-1&&tr.cc<costmin&&arr[tr.x[0]][tr.x[tr.n-1]]!=MAX)
            {
                
                for(int i=0;i<arr.length-1;i++)
                {
                    route[i]=tr.x[i];
                }
                route[arr.length-1]=route[0];
            }
            
            for(int i=1;i<arr.length;i++)
            {
                if(cc>costmin)
                    break;
                if(tr.flag[i]==0&&arr[end][i]!=MAX&&cc<costmin)
                {
                    int xtmp[]=new int[arr.length-1];
                    for(int j=0;j<tr.n;j++)
                    {
                        xtmp[j]=tr.x[j];
                    }
                    xtmp[tr.n]=i;
                    int flagtmp[]=new int[arr.length];
                    for(int j=0;j<arr.length;j++)
                    {
                        flagtmp[j]=tr.flag[j];
                    }
                    flagtmp[i]=1;
                    traveling addr=new traveling(cc+arr[end][i], xtmp, tr.n+1, flagtmp);
                    if(tr.n+1==size-1&&cc+arr[end][i]+arr[i][tr.x[0]]<costmin)
                        costmin=cc+arr[end][i]+arr[i][tr.x[0]];
                    q.offer(addr);
                }
            }
        }
    }
}