这道题是困难题,本章是针对于动态规划解决,对于思路进行一个全面透彻的讲解,但是并不是对于基础讲解思路,而是渗透到递推式和dp填数的详解,如果有读者不清楚基本的解题思路,请看我的这篇文章算法训练营DAY53|392.判断子序列、115.不同的子序列-CSDN博客
但在看的过程中,你可能会有为什么把dp数组设为以i-1和j-1的下标这样的奇怪含义的困惑,这是为了方便初始化,不用对每一个位置进行一开始的判定初始化,也就是说可能要对于一开始下标匹配做一些多余的处理,详细的解释可以翻看我往期作品,其中会有更为详细的介绍,本期文章,我主要是针对,对于思路有一些了解,但是对于题解本身仍存有一些疑惑的读者准备的。
当然也是对于 我之前写的那期题解未能写的清楚的一些部分的补充。
这里还要纠正一下第一次写那个题解的一部分话是存在一些问题的,两个字符匹配的第一项并不是未匹配成功的结果,如果读者不能明白我在说什么直接看下面的代码即可,不必要去看那期文章,以避免误导读者。
class Solution {
public:
int numDistinct(string s, string t) {
int m=s.size(),n=t.size();
vector<vector<uint64_t>>dp(m+1,vector<uint64_t>(n+1,0));
for(int i=0;i<=m;++i)dp[i][0]=1;
for(int i=1;i<=m;++i){
for(int j=1;j<=n;++j){
if(s[i-1]==t[j-1])dp[i][j]=dp[i-1][j-1]+dp[i-1][j];
else dp[i][j]=dp[i-1][j];
}
}
return dp[m][n];
}
};如上是题目正确的代码,可以ac。
首先我们来分析的是递推式,然后是初始化和打表,最后是整体的总结。
先粘上一张代码随想录的图片,当大家需要看图对比时候可以回过头开看:
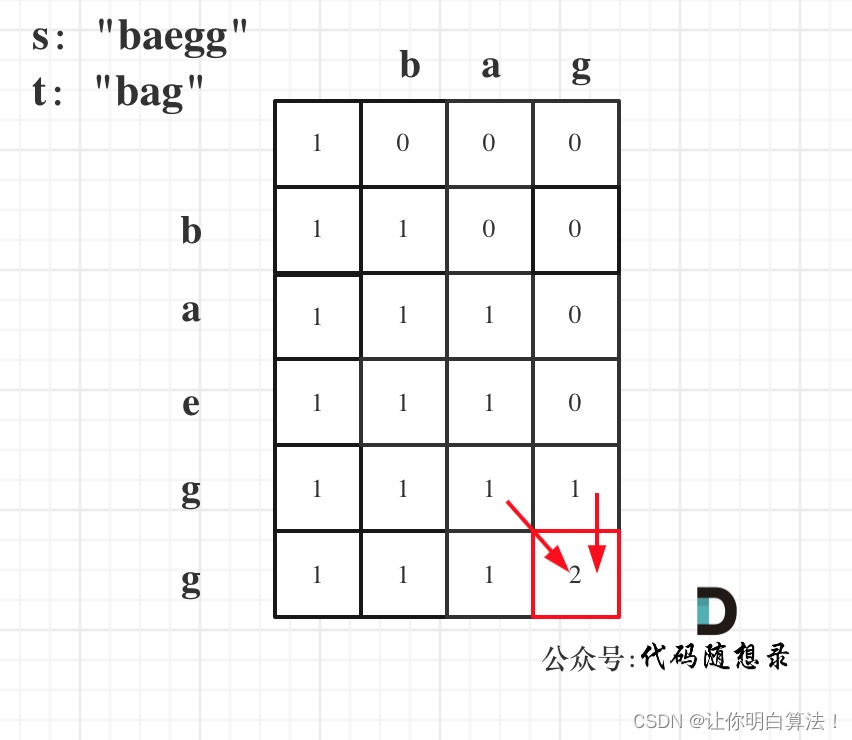
请注意:子序列问题中dp解决时,通常在需要在两个数组或字符串中找答案时候,大多数情况下都需要开辟二维dp数组来解决问题。
明确递推式dp【i】【j】代表以i-1和j-1结尾的字符串s和t,当前情况下,s字符串中t出现的个数有多少个。
递推公式:当i-1和j-1位置上的s和t字符串对应下标字符相等,则当前位置可由dp【i-1】【j-1】推出来,这个递推式的意思是由于这两个字符相等所以不用管该两个字符,
然后去看相当于i-2和j-2对应的位置下,s中包含了多少个t。
你也可以理解为当前的dp【i】【j】要填数,就要看上一个状态时,也就是dp【i-1】【j-1】的状态,因为此时对应下标的元素相等,所以直接去看上一个状态,而此时不需要删除元素
那上一个状态dp【i-1】【j-1】有没有可能需要删除元素呢?当然有可能,但这并不是我们本次填数需要解决的问题,上一个状态肯定在上一个状态被解决了。
为什么不是dp【i-1】【j-1】+1?当前字符相等应该意味着我们又多匹配成功了一个字符,所以理应+1啊
看这两个【bag】和【bag】当该填数dp【2】【2】时候,我们根据dp数组定义实际上看的是s的i-1下标,和t的j-1下标位置
那么也就是此时正在比较【ba】和【ba】呢,它的上一个状态是【b】【b】虽然匹配是相等,但是这并不意味着我们只要匹配相等字符就得+1
因为这道题求的不是重复字符最多有多少个!!!
那怎么完成匹配成功t字符串时候加入答案呢?因为有第二项递推式!
是dp【i-1】【j】这个递推式就相当于不回退当前的t字符串的匹配下标,而是回退s字符串下标,看看此时状态是否有s中有t字符串的这种情况
举例:【bagg】和【bag】这两个,那么除了s字符中的s[0]s[1]s[3]可以得到t字符串,s[0]s[1]s[2]这个组合也可以得到t字符串。
所以这正是我们可以回退s的原因,换个角度去看,这也是我们匹配t这个字符串的整个字符串的方法。把这两个递推式相加就可以得到dp【i】【j】了
我们不考虑t字符串回退的原因,在这里是因为我们是在s字符串里找有多少个t,而不是在t里找,所以应该回退s里的字符。如果你选择回退t此时对应的下标,那么将不可能得到正确答案,因为无论最后s能不能
从中找到t字符串的完整序列,只要t中的部分子数组在s中出现过,那么它一直沿用前面的状态,那是不是肯定会得到1次匹配?
你想想t一直沿用前面的状态,而最开始的状态是s有字符而t无字符,所以一定会有一解。这得出的答案一定是错误的。
所以t不可回退字符,t只能向前匹配,这样保证了求到最后的是s里是否包含完整的t字符串,而不是只要包含一部分子数组就可以完成匹配。
还有一件事是:s字符下标每次增大1然后重新对t字符串进行匹配,也就解决了以各个的s下标位置为截止,能匹配到最大匹配个数是多少。将它们加起来就是答案。
而如果此时两字符对应不等怎么办
dp【i】【j】=dp【i-1】【j】这里的递推式你可以理解为,删除s字符串当前遍历的字符(模拟删除)而转为用该下标的前一个位置看看有没有
s中含有t的时候,延续那时候的状态就可以了。
初始化也很重要它是得到答案的关键初始化dp数组,s和t数组都为空时候对应dp应该为1,解释:两字符串都为空,则s字符串里包含1个t
当s字符串有内容,t为空,那么s各个状态都为1,解释:s字符串删除全部字符得到空字符串也就是t
当s没内容,t有内容,则这些状态都为0,解释:s无论如何也无法推出t
当两字符串内容不相等时候,也就是s中不包含t那么无论如何也推不出一个,因为s里要想能找到t,那么必须t中的第一个元素与s中的某位置元素发生了起始匹配。
这时初始化产生作用,虽然这种中间某处得到的匹配,匹配不上原始的dp【0】【0】但是它能匹配上dp【i】【0】使得累计1次匹配。
然后接下来的匹配,就是对t字符串各个字符都必须连续匹配,才可以使这个1继承下来,因为递推式的缘故,往后匹配,dp【0】【0】肯定匹配不上
而如果中间某字符没匹配上断档了,那么再匹配上的时候,dp【i-1】【j】也不可能借用到dp【i】【0】就使得最终答案是0。
打表特殊测试用例 s=【bag】t=【bag】
dp[0][0]=1dp[0][1]=0dp[0][2]=0dp[0][3]=0
dp[1][0]=1dp[1][1]=1dp[1][2]=0dp[1][3]=0
dp[2][0]=1dp[2][1]=1dp[2][2]=1dp[2][3]=0
dp[3][0]=1dp[3][1]=1dp[3][2]=1dp[3][3]=1
可见即使中间遍历时候也有完全匹配时候【ba】【ba】但是这并不会使dp【2】【2】变成2
由头上的图片可以知道其实dp【i-1】【j-1】和dp【i-1】【j】都有可能是答案的组成部分
打表bac和bad
dp[0][0]=1dp[0][1]=0dp[0][2]=0dp[0][3]=0
dp[1][0]=1dp[1][1]=1dp[1][2]=0dp[1][3]=0
dp[2][0]=1dp[2][1]=1dp[2][2]=1dp[2][3]=0
dp[3][0]=1dp[3][1]=1dp[3][2]=1dp[3][3]=0
再写该题时候,写到循环部分的时候,想的是t字符串既然不能使之回退,那么是不是应该写成t循环在外面,s循环在里面,这样只循环了一次t,就保证了不回退的效果,而不是写成s循环在外面t循环在内部
但后来发现不是这么一回事,这样写循环是有原因的,它遍历s的各个字符给t去进行匹配,以获得所有的组合答案。如果t循环写外面了,t确实没有回退,但是这样写的思路不就成了拿t的各个元素去找
t里面是否存在s字符串了吗?这不就写反了吗?
还有就是外层for是s内层for是t,并不是没有实现t的禁止回退,所谓t字符串不能回退不是指t的字符串不能重复遍历,不能回退体现在递推公式上,不要弄混淆。
再细说一下具体的匹配机理,是如何实现s拿一个个字符串然后去匹配t的。
首先s字符串每次增大一个匹配范围(表面上看),然后t字符串在s每次增大匹配范围时,重新遍历t字符串去和s的现在范围去匹配,看看现在的s范围能否找到更多的匹配次数并填到dp数组内。
从代码的实际运行角度,s的每次增大一个字符的范围,t重新匹配,并不是匹配0——i,而是拿t的整个字符串去和i这个元素单单去匹配,而非s子串和t字符串匹配。
这实际上无形之中提升了效率,那么怎么实现匹配的正确呢?
递推式已经给出了,如果当前元素匹配不上,那么当前位置填数继承上一次匹配,也就是当前两个字符不匹配,那么相当于放弃当前两个字符的匹配机会,而是选用上一次的对应截止字符处,去继承那一次的
匹配成果。这次的继承是就是回退s而不回退t
如果匹配成功,有两个方向推出,一个是不考虑当前两个字符,因为两个字符当前匹配成功,所以暂时不考虑,但是还没完,还要考虑s往前回退一个字符的情况与t进行匹配的成果,将二者相加得到答案
为什么不回退第二个字符串t我们上面已经说得很清楚了,而回退s为上一个字符是为什么呢?就是因为bag和bagg的测试用例这类情况,也即是说可能存在上一个s的字符也存在匹配的关系,那有人要问
如果是bag和baggg呢?你怎么匹配?这是一样的,第二次的g会继承第一次g匹配成果,而第三次又会继承第二次.看递推式就能知道,两字符匹配成功,答案是左上角数加上头上的数,
而这个头上的数,自然把上一层的g加过来了。
还有一个问题是为什么总是能得到正确答案,我们上面已经说了一些了,但是个人觉得还不够透彻。再说一次
首先它为什么不是每匹配成功一次都+1我们上面说的很清了,当两个字符相等时候的填数再说一下
我们由于初始化的缘故,使得若此时匹配的两个字符匹配不相等,也就是说假如bagg和bag,s字符串bagg匹配到最后一个字符时候,但是t字符串从头开始匹配,这个时候我们由于第二递推式,匹配不等时候会拿
dp【i】【j-1】的数做继承,直到匹配成功填数的时候,真正的递推作用才开始显现
匹配相等时,会把头上的位置也就是dp【i-1】【j】和dp【i-1】【j-1】累加起来,换句话说只有两个字符最后发生匹配时候,才能够获得答案,如果不发生匹配不会获得答案。
这是为什么呢?不是说不匹配会继承前位置吗?但是你要注意,只有同列才能继承,也就是说如果你的上一行列没有做事,那么你不能享受成果,这就相当于祖上得有财富积累,你才能躺平拿到成果,否则你只能
依赖于本身的才能,也就是进入第一递推式,虽然祖上可能没有成果,但你可以收获你左上角人的成果。
所以并不会发生一处匹配成功,全部人都受益的结果。
你左上的成果相当于叔辈的成果,你没有能力时候它不会贡献成果给你享用,只有你的亲祖先才能共享成果,所以如果前面出现多次匹配,也就是说祖先和叔辈都得到了匹配,或他们继承它们的祖先和叔辈匹配
而且同时你也有能力匹配,才会同时得到两方面的匹配成果。
这个左上角匹配也并非与你完全无关,它有数字代表了发生连续匹配。
badgbacg打表
dp[0][0]=1dp[0][1]=0dp[0][2]=0dp[0][3]=0dp[0][4]=0
dp[1][0]=1dp[1][1]=1dp[1][2]=0dp[1][3]=0dp[1][4]=0
dp[2][0]=1dp[2][1]=1dp[2][2]=1dp[2][3]=0dp[2][4]=0
dp[3][0]=1dp[3][1]=1dp[3][2]=1dp[3][3]=0dp[3][4]=0
dp[4][0]=1dp[4][1]=1dp[4][2]=1dp[4][3]=0dp[4][4]=0
这下应该明白了吧,虽然祖上有成果的某些中间量会继承祖上的成果,但这并不一定影响最后的答案,该样例中即使最后一次发生了g和g的匹配,但是它的左上角没有成果也就是出现了断档,而且它的祖上也没有
成果,所以它依然无法收获结果。
这也就是说只要中间断档发生了一次,那么就不再可能延续的上,想尝试的读者可写一个badgh和bacgh试一下打表
简而言之:
对于当前两字符匹配成功,则需要收获结果,结果的第一部分代表了之前字符的连续匹配,第二部分代表了s中存在多个t的继承匹配个数
对于匹配不成功,继承连续匹配结果,这一举动主要是为了下一次的s扩大后的匹配受益,因为s当前字符不可能与t所有字符匹配,那么只要有一次完成了匹配,则这一列的所有位置理应继承那次匹配成功的成果。
以应对下一次循环匹配的时候,对于连续字符匹配的连贯性。
相信如果读者事先具备了代码思路,知道题解如何解答,再看这篇文章一定会受益匪浅。
这是对于细节上问题的一些补充。本章就到这里。
都看到这里了如果对您有用的话别忘了一键三连哦,如果是互粉回访我也会做的!
大家有什么想看的题解,或者想看的算法专栏、数据结构专栏,可以去看看往期的文章,有想看的新题目或者专栏也可以评论区写出来,讨论一番,本账号将持续更新。
期待您的关注