Adversarial Attacks on Neural Networks for Graph Data

Adversarial Attacks on Neural Networks for Graph Data----《针对图数据的神经网络的对抗攻击》

论文提出了两个问题：

1、属性图的深度学习模型容易受攻击吗？
2、他们的结果可靠吗？

回答这两个问题需要考虑到GNN的特性：

①关系效应：图中的预测不止是基于单个实例，而是基于各种实例的联合。
②消息传播机制：操纵一个实例会影响许多其他实例。

摘要

基于图的深度学习模型在节点分类任务上取得了较好的性能。尽管已经有了很多成果，但目前还没有研究它们对敌对攻击的鲁棒性。然而，在可能使用它们的领域，例如在网络上，对手很常见。图的深度学习模型容易被愚弄吗？ 在这项工作中，我们介绍了对属性图的对抗性攻击的第一个研究，特别关注利用图卷积思想的模型。除了测试时的攻击外，我们还解决了更具挑战性的中毒/致病攻击，这些攻击集中在机器学习模型的训练阶段。因此，在考虑实例之间的依赖关系的情况下，我们针对节点的特征和图结构产生对抗扰动。此外，我们通过保留重要的数据特征来确保扰动不被察觉。为了处理底层的离散域，我们提出了一种利用增量计算的高效算法Nettack。我们的实验研究表明，即使只执行少量的扰动，节点分类的准确性也显著下降。更重要的是，我们的攻击是可转移的：学习到的攻击可推广到其他最先进的节点分类模型和无监督方法，即使只给出有限的图知识，同样也能成功。

引言

图表数据是许多高影响力应用程序的核心，包括分析社交和评级网络(Facebook、亚马逊)、基因交互网络(BioGRID)，以及相互链接的文档集合(PubMed、Arxiv)。图数据上最常用的任务之一是节点分类：给定一个大型(属性化的)图和少数节点的类标签，目标是预测剩余节点的标签。例如，人们可能希望对生物相互作用图[18]中的蛋白质角色进行分类，预测电子商务网络[13]中的用户类型，或将引文网络中的科学论文分配到主题[20]中。虽然过去已经引入了许多经典的方法来解决节点分类问题[8,22]，但在过去的几年里，人们对图的深度学习方法产生了极大的兴趣[5,7,26]。具体来说，来自图卷积网络的方法[20,29]在包括节点分类在内的许多图学习任务中都取得了很强的性能。
这些方法的优势——超越了其非线性、分层的本质——依赖于它们对图的关系信息的使用来执行分类：除了单独考虑实例(节点及其特性)外，还利用了它们之间的关系(边)。换句话说：实例不是独立处理的；我们处理某种形式的非独立同分布。所谓的网络效应（例如同质性[22]）支持分类的数据。
然而，有一个大问题：许多研究人员注意到，经典学习任务的深度学习架构很容易被愚弄/攻击 [15, 31]。即使只是对实例进行轻微的、故意的扰动（也称为对抗性扰动/示例），也可能导致错误的预测。这种负面结果极大地阻碍了这些模型的适用性，导致不直观和不可靠的结果，并且还为攻击者利用这些漏洞打开了大门。然而，到目前为止，图深度学习方法的对抗性扰动问题尚未得到解决。这是非常关键的，因为特别是在使用基于图的学习的领域（例如网络），对手很常见，并且很容易注入虚假数据：如垃圾邮件发送者向社交网络添加错误信息；欺诈者经常操纵在线评论和产品网站[19]。
属性图的深度学习模型容易被愚弄吗？他们的结果有多可靠？ 这个问题的答案确实是不可预见的：一方面，关系效应可能会提高鲁棒性，因为预测不仅仅基于单个实例，而是共同基于多个实例。另一方面，信息的传播也可能导致级联效应，即操纵一个实例会影响许多其他实例。与现有的对抗性攻击工作相比，该工作在各个方面都有很大的不同。
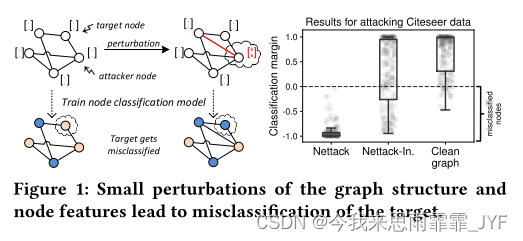
机会：(1)由于我们是在一个带属性的图上操作，对抗扰动可以通过两种不同的方式表现出来：通过改变节点的特征或图的结构。操纵图，即实例之间的依赖结构，到目前为止还没有研究过，但在现实生活中是很可能出现的场景。例如，人们可以在社交网络中添加或删除友谊关系。(2)虽然现有的工作仅限于操纵一个实例本身，以加强其错误的预测，但关系效应给了我们更多的力量：通过操纵一个实例，我们可能会专门误导对另一个实例的预测。同样，这个场景是非常现实的。想象一下一个欺诈者劫持了一些账户，然后他操纵这些账户对他无法控制的另一个账户强制执行错误的预测。因此，在基于图的学习场景中，我们可以区分（i）我们旨在错误分类的节点（称为目标）和（ii）我们可以直接操纵的节点（称为攻击者）。图 1 说明了我们工作的目标，并显示了我们的方法在 Citeseer 网络上的结果。显然，与DNN学习模型的经典攻击相比，图具有更丰富的扰动潜力。但同样，构建它们也更具挑战性。
在这里插入图片描述
挑战：(1) 与图像等由连续特征组成的数据不同，图结构（通常还有节点的特征）是离散的。因此，基于梯度的方法 [15, 24] 不适合寻找扰动。如何设计能够在离散域中找到对抗样本的有效算法？(2) 对抗性扰动的目的是不被人类察觉。对于图像，通常会强制执行例如每个像素值的最大偏差。我们如何捕捉（二元、属性）图中“不明显的变化”的概念？(3)最后，节点分类通常在转导学习环境（指模型在一个任务上学到的知识被迁移到另一个相关或不同的任务上）中进行。在这里，在对特定的测试数据进行预测之前，将训练数据和测试数据联合学习一个新的分类模型。这意味着，主要执行的逃避攻击——分类模型的参数被假定为静态的——是不现实的。模型必须对被操纵的数据进行(重新)训练。因此，转导环境中基于图的学习本质上与具有挑战性的中毒/致病攻击相关[3]。
考虑到这些挑战，我们提出了一种属性图的对抗性扰动原则，旨在欺骗最先进的图深度学习模型。我们特别关注基于图卷积的半监督分类模型，如GCN[20]和Column Network (CLN)[29]，同时我们也将展示我们的方法在无监督模型DeepWalk[28]上的潜力。默认情况下，我们假设攻击者知道完整的数据，但是，攻击者只能操作其中的一部分。这种假设可确保在最坏的情况下进行可靠的漏洞分析。但正如我们的实验所示，即使只知道部分数据，我们的攻击仍然是成功的。总的来说，我们的贡献是：

模型：我们提出了一种考虑节点分类的属性图对抗性攻击模型。我们引入了新型攻击，我们明确区分攻击者和目标节点。我们的攻击可以操纵图结构和节点特征，同时通过保留重要的数据特征（例如度分布、特征共现）来确保不明显的变化。
算法：我们开发了一种基于线性化思想的高效算法Nettack来计算这些攻击。我们的方法支持增量计算，并利用图的稀疏性快速执行。
实验：我们表明，我们的模型可以通过只需要对图进行很少的更改来显著地恶化目标节点的分类结果。我们进一步表明，这些结果可以转移到其他已建立的模型，适用于各种数据集，甚至当只有部分数据被观察时也有效。总的来说，这凸显了处理图数据攻击的必要性。

符号表示

令 $G = (A, X)$ 为属性图

$\in {\{ 0,1\} ^{N \times N}}$ 为邻接矩阵

$\in {\{ 0,1\} ^{N \times D}}$ 为节点特征（这里为二进制节点特征）

$N$ 个节点，单个节点可表示为 ${x_v} \in {\{ 0,1\} ^D}$ ， $D$ 为特征长度

$V = \{ 1,...,N\}$ ， $F = \{ 1,...,D\}$

带标签节点 ${v_L} \subseteq V$ ，分类函数 $\to C$

类别 $C$ 为 $C = \{ {c_1},{c_2},...,{c_k}\}$

实验模型使用两层GCN： ${f_\theta }(A,X) = soft\max (\hat A\sigma (\hat AX{W^{(1)}}){W^{(2)}})$

其中： $\hat A = {D^{ - \frac{1}{2}}}\tilde A{D^{ - \frac{1}{2}}}$ ， $\tilde A = A + {I_N}$

交叉熵损失： $L(\theta ;A,X) = - \sum\limits_{v \in {v_L}} {In{z_{v,{c_v}}}}$

攻击模型

目的：对图 ${G^{(0)}} = ({A^{(0)}},{X^{(0)}})$ 进行小扰动

在图 ${G^{(0)}}$ 上增加小扰动后得到扰动图 $G^{'} = (A^{'}, X^{'})$ 使得分类性能下降

对 ${A^{(0)}}$ 的更改称为结构攻击，对 ${X^{(0)}}$ 的更改称为特征攻击

目标：攻击特定目标节点 ${v_0} \in V$ ，即改变 ${v_0}$ 的预测

攻击者： ${\rm A} \subseteq V$ （ ${\rm A}$ 为攻击者节点）

扰动限制（对于节点）： ${X'_{ui}} \ne X_{ui}^{(0)} \Rightarrow u \in {\rm A}$ ， ${A'_{uv}} \ne A_{uv}^{(0)} \Rightarrow u \in {\rm A} \vee v \in {\rm A}$ （1）

if $\{ {v_0}\} = {\rm A}$ 称为直接攻击， ${v_0} \notin {\rm A}$ 称为影响者攻击， ${v_0}$ 没有被直接操纵

扰动量限制： $\sum\limits_u {\sum\limits_i {\left| {X_{ui}^{(0)} - {{X'}_{ui}}} \right| + \sum\limits_{u < v} {\left| {A_{uv}^{(0)} - {{A'}_{uv}}} \right| \le \Delta } } }$ （2）

用 ${\rm P}_{\Delta ,{\rm A}}^{{G^{(0)}}}$ 表示所有满足（1）、（2）的 $G^{'}$

问题定义：已知 ${G^{(0)}} = ({A^{(0)}},{X^{(0)}})$ ，目标节点 ${v_0}$ ，攻击者节点 ${\rm A}$ ， ${v_0}$ 的真实类别 ${c_{old}}$

使得 ${\mathop {\arg \max }\limits_{(A',X') \in {\rm P}_{\Delta ,{\rm A}}^{{G^{(0)}}}} \mathop {\max }\limits_{c \ne {c_{old}}} Inz_{{v_0},c}^* - Inz_{{v_0},{c_{old}}}^*}$ ，

其中， ${z^*} = {f_{{\theta ^*}}}(A',X')$ ， ${\theta ^*} = \mathop {\arg \min }\limits_\theta L(\theta ;A',X')$

也就是说，目的是找到一个扰动图 $G^{'}$ ，将 ${v_0}$ 分类为 ${c_{new}}$ ，且与 ${c_{old}}$ 具有最大“距离”。因此，下面的问题就变成了寻找影响模型预测且不被感知的扰动。

不明显的扰动

通常，在对抗性攻击场景中，攻击者尝试修改输入数据，以使更改不明显。与图像数据不同，在图像数据中，这可以通过视觉和使用简单的约束来轻松验证，在图形设置中，这要困难得多，主要有两个原因：(i)图的结构是离散的，不能使用无穷小的小变化，(ii)足够大的图不适合视觉检查。
我们如何确保我们设置的扰动不被注意到?特别是，我们认为，仅考虑Δ预算可能是不够的。特别是如果由于数据复杂而需要较大的 Δ，我们仍然希望看到逼真的扰动图𝐺′。因此，我们的核心思想是只允许那些保留输入图特定固有属性的扰动。

图结构保留扰动

毫无疑问，图结构最显著的特征是它的度分布，在实际网络中，度分布往往类似于幂律形状。如果两个网络显示出非常不同的度分布，很容易将它们区分开来。因此，我们的目标是仅生成遵循与输入类似的幂律行为的扰动。为此，我们参考幂律分布的统计双样本检验[2]。也就是说，我们使用似然比检验来估计 𝐺 (0) 和 𝐺′ 的两个度分布是来自于相同的分布还是来自于单个的分布。
首先根据 ${G^{(0)}}$ 的度分布估计幂律分布 $p(x)\infty {x^{ - \alpha }}$ 的尺度参数𝛼，并且对 $G^{'}$ 采取同样的操作。虽然在离散数据的情况下没有精确且封闭的解决方案来估计 $\alpha$ ，但 [10] 导出了一个近似表达式，对于我们的图 $G$ 来说，它可以转换为

${\alpha _G} \approx 1 + \left| {{D_G}} \right| \cdot {\left[ {\sum\limits_{{d_i} \in {D_G}} {\log \frac{{{d_i}}}{{{d_{\min }} - \frac{1}{2}}}} } \right]^{ - 1}}$

其中， ${d_{\min }}$ 表示节点的最小度数， ${D_G}$ 表示节点度数列表

${D_G} = \{ d_v^G|v \in V,d_v^G \ge {d_{\min }}\}$

$d_v^G$ 表示节点 $v$ 在 $G$ 中的度数

给定缩放参数 ${\alpha _x}$ ，样本 ${D_x}$ 的对数似然为：

$l({D_x}) = \left| {{D_x}} \right| \cdot \log {\alpha _x} + \left| {{D_x}} \right| \cdot {\alpha _x} \cdot \log {d_{\min }} - ({\alpha _x} + 1)\sum\limits_{{d_i} \in {D_x}} {\log {d_i}}$

使用这些对数似然分数，我们设置显着性检验，估计两个图 D𝐺 (0) 和 D𝐺′ 是否来自相同的幂律分布（空假设 ${H_0}$ ），而不是单独的幂律分布（ ${H_1}$ ）。也就是说，我们提出两个相互竞争的假设：

$l({H_0}) = l({D_{comb}})$ ， ${D_{comb}} = {D_{{G^{(0)}}}} \cup {D_{G'}}$ ， $l({H_1}) = l({D_{{G^{(0)}}}}) + l({D_{G'}})$

经过似然比检验后，最终的检验统计量为：

$\Lambda ({G^{(0)}},G') = - 2 \cdot l({H_0}) + 2 \cdot l({H_1})$

满足度分布的扰动： $\Lambda ({G^{(0)}},G') < \tau \approx 0.004$

节点特征保留扰动

虽然上述原则也可以应用于节点的特征(例如，保持特征出现的分布)，但我们认为这样的过程太有限了。特别是，这样的测试不能很好地反映不同特征的相关性/共现性：如果两个特性在 ${G^{(0)}}$ 中从未同时出现，如果两个特征从未在 ${G^{(0)}}$ 中同时出现，但在 $G^{'}$ 中出现过一次，则特征出现的分布仍然非常相似。然而，这种变化很容易被注意到。例如，考虑两个从未一起使用过但突然在 $G^{'}$ 中使用的单词。因此，我们称之为基于特征共现的测试。
由于设计基于共现的统计检验需要对特征上的联合分布进行建模——这对于相关的多元二进制数据[25]是难以处理的——因此我们使用确定性检验。在这方面，将特征设置为 0 并不重要，因为它不会引入新的共现。问题是：节点𝑢的哪些特征可以设置为1而被视为不明显？
为了回答这个问题，我们在 ${G^{(0)}}$ 的特征的共现图 $C = (F, E)$ 上考虑概率随机游走，即 $F$ 是特征的集合， $\subseteq F \times F$ 表示到目前为止哪些特征同时出现。我们认为，如果一个随机游走者从节点 $u$ 的初始特征开始，经过一步就能显著大概率地到达添加的特征 $i$ ，那么添加特征 $i$ 是不容易察觉的。形式上，令 ${S_u} = \{ j|{X_{uj}} \ne 0\}$ 是节点 $u$ 最初存在的所有特征的集合。我们认为将特征 $\notin {S_u}$ 添加到节点 $u$ 是不明显的，如果

$p(i|{S_u}) = \frac{1}{{\left| {{S_u}} \right|}}\sum\limits_{j \in {S_u}} {1/{d_j} \cdot {E_{ij}} > \sigma }$

使用上述测试，我们只接受特征值满足的扰动 𝐺′ = (𝐴′, 𝑋′)

${\forall _u} \in V:{\forall _i} \in F:{X'_{ui}} = 1 \Rightarrow i \in {S_u} \vee p(i|{S_u}) > \sigma$

生成对抗图

解决问题 1/2 非常具有挑战性。尽管在过去的研究中已经通过基于一阶KKT条件的梯度计算来解决攻击的（连续）双层问题[21, 24]，但在我们的例子中，由于数据的离散性和大量的参数𝜃，这样的解决方法是不可能的。因此，我们提出了一种顺序方法，首先攻击代理模型，从而产生被攻击的图。这个图随后被用来训练最终的模型。事实上，这种方法可以直接被看作是对可迁移性的检验，因为我们不专门关注所使用的模型，而只关注一个替代模型。

代理模型

为了获得一个仍能捕捉图卷积思想的易于处理的代理模型，我们对模型进行线性化。即我们将非线性𝜎(.)替换为一个简单的线性激活函数，得到:

$soft\max (\hat A\hat AX{W^{(1)}}{W^{(2)}}) = soft\max ({\hat A^2}XW)$

Softmax函数是一种非线性激活函数，在某种程度上它可以在二分类问题中起到类似线性激活函数的作用。
由于我们的目标是最大化目标 𝑣0 的对数概率差异（给定一定的预算 Δ），因此可以忽略由 softmax 引起的依赖于实例的归一化。因此，对数概率可以简单地减少到 ${\hat A^2}XW$ 。因此，鉴于在（未受损）输入数据上训练的具有学习参数 𝑊 的替代模型，我们定义了替代损失：

${L_s}(A,X;W,{v_0}) = \mathop {\max }\limits_{c \ne {c_{old}}} {[{\hat A^2}XW]_{{v_0}c}} - {[{\hat A^2}XW]_{{v_0}{c_{old}}}}$

并且目标是解决： $\mathop {\arg \max }\limits_{(A',X') \in \hat p_{\Delta ,{\rm A}}^{G0}} {L_s}(A',X';W,{v_0})$

虽然要简单得多，但由于离散域和约束，这个问题仍然难以精确解决。因此，下面我们介绍一种可扩展的贪婪近似方案。为此，我们定义了评分函数来评估方程式中的替代损失。在任意图 𝐺 = (𝐴, 𝑋) 上添加/删除特征 𝑓 = (𝑢, 𝑖) 或边 𝑒 = (𝑢, 𝑣) 后获得：

${s_{struct}}(e;G,{v_0}): = {L_s}(A',X;W,{v_0})$

${s_{feat}}(f;G,{v_0}): = {L_s}(A,X';W,{v_0})$

其中： $\pm e$ ， $\pm f$

近似解

算法1展示了伪代码。具体而言，遵循局部最优策略，我们按顺序“操作”最有希望的元素：要么是邻接矩阵的一个条目，要么是特征条目（考虑到约束条件）。
在这里插入图片描述

快速计算评分函数和候选集的快速计算（可以见原文，都是公式的推导）

实验

我们探索我们的攻击如何影响代理模型，并评估向其他模型和多个数据集的可转移性。Nettack 的源代码可在我们的网站上获取：https://www.daml.in.tum.de/nettack。
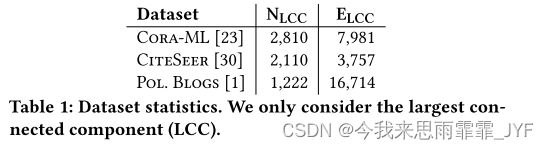
我们使用了[5]中使用的著名的Cora-ML和Citeseer网络，以及Polblogs [1]。数据集特征如表1所示。我们将网络分为标记节点（20%）和未标记节点（80%）。我们进一步将标记节点分成等份的训练集和验证集来训练我们的代理模型。也就是说，我们在训练过程中从验证集中删除标签，并将它们用作停止标准（即，当验证误差增加时停止）。在训练期间，代理模型永远看不到未标记节点的标签。
在这里插入图片描述
我们对5个不同的随机初始化/拆分进行平均，其中每个初始化/拆分都执行以下步骤。我们首先在标记数据上训练代理模型，并在测试集中已正确分类的所有节点中，选择 (i) 分类余量最高的 10 个节点，即它们被明确正确分类，(ii) 这 10 个节点边缘最低的节点（但仍然正确分类）和（iii）随机另外 20 个节点。这些将作为我们攻击的目标节点。然后，我们使用本工作中提出的模型破坏输入图，分别称为 Nettack 用于直接攻击和 Nettack-In 用于影响攻击（从目标的邻域中选择 5 个随机节点作为攻击者）。
由于不存在其他竞争对手，我们与两个基线进行比较：（i）快速梯度符号方法（FGSM）[15]作为对𝑣0的直接攻击（在我们的例子中还确保结果仍然是二进制的）。(ii) Rnd 是一种修改图结构的攻击。给定我们的目标节点 𝑣0，在每一步中，我们随机采样节点 𝑢，其中 𝑐𝑣0 ≠ 𝑐𝑢，并将边 𝑢、𝑣 添加到图结构中，假设不相等的类标签阻碍分类。

对代理模型的攻击

我们首先通过检查它们对代理模型的影响来分析我们方法的不同变体。在图 2（左）中，我们绘制了执行特定数量的扰动时的替代损失。请注意，一旦代理损失为正，我们就实现了成功的错误分类。我们分析 Nettack 以及仅操作特征或仅操作图结构的变体。如图所示，与特征攻击相比，结构中的扰动会导致代理损失发生更大的变化。尽管如此，将两者结合起来是最强大的，只需要大约 3 次更改即可获得错误分类。为了进行比较，我们还添加了 Rnd，这显然无法实现良好的性能。
在图 2（右）中，我们分析了使用直接攻击与影响者攻击时的方法。显然，直接攻击需要较少的扰动——尽管如此，影响者攻击也是可能的，在现实生活中构成很高的风险。该图还显示了不使用第 4.1 节中建议的约束时的结果，由名称 Nettack-U 表示。正如所见，即使使用我们的约束，攻击仍然成功。因此，可能会产生不明显的扰动。
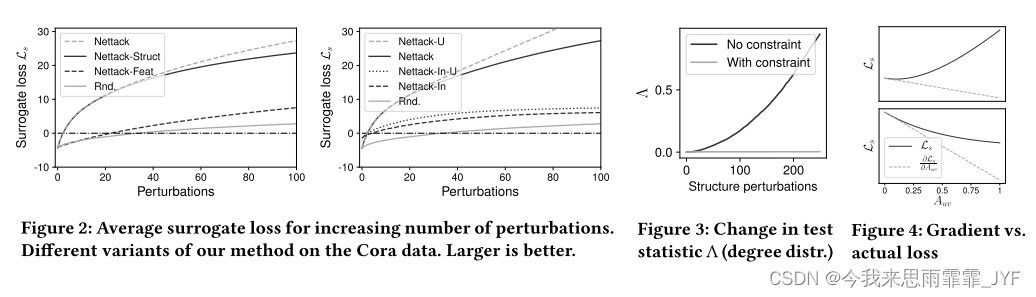
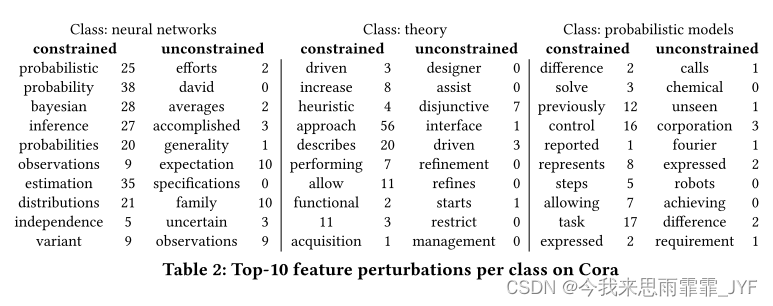
在这里插入图片描述
值得一提的是，约束确实是必要的。图 3 显示了在有或没有我们的约束的情况下结果图的检验统计量 Λ。正如所见，我们施加的约束会对我们的攻击产生影响；如果不强制执行，损坏的图的幂律分布将变得与原始图越来越不相似。同样，表 2 说明了特征扰动的结果。对于 Cora-ML，这些特征对应于论文摘要中单词的存在。对于每个类（即具有相同标签的节点集），我们绘制了通过这些技术操纵的前 10 个特征（这些特征约占所有扰动的 50%）。此外，我们报告每个特性在类中的原始出现情况。我们看到使用的特征确实不同——更重要的是，无约束版本经常使用对于该类“不太可能”的单词（由小数字表示）。使用这些词很容易被发现是在操纵，例如神经网络中的“大卫”或概率模型中的“化学”。我们的约束确保变化更加微小。
在这里插入图片描述
总的来说，我们的结论是，同时攻击特征和结构是非常强大的；并且引入的约束不会阻碍攻击，同时会产生更真实的扰动。直接攻击显然比影响者攻击更容易。

攻击的可转移性

在探索我们的攻击如何影响（固定）代理模型之后，我们现在将了解我们的攻击在已建立的图深度学习模型上是否也成功。为此，我们采用之前的方法并使用预算 Δ = 𝑑𝑣0 +2，其中𝑑𝑣0 是我们当前攻击的目标节点的程度。这是由于观察到高度节点比低度节点更难受到攻击。

对抗vs中毒攻击

在图 6a 中，我们评估了 Nettack 对两种攻击类型的性能：对抗攻击，其中模型参数（此处为 GCN [20]）基于干净的图保持固定；中毒攻击，模型在攻击后重新训练（平均运行 10 次以上）。在图中，每个点代表一个目标节点。正如所见，直接攻击非常成功——即使对于具有挑战性的中毒攻击，几乎每个目标都被错误分类。因此，我们得出结论，在对扰动数据进行重新训练后，我们的代理模型和损失足以近似非线性模型的真实损失。显然，影响者攻击（双线右侧所示）更加困难，但在这两种情况下仍然有效。由于中毒攻击通常更难并且更适合迁移学习场景，因此我们在下面仅报告这些结果。
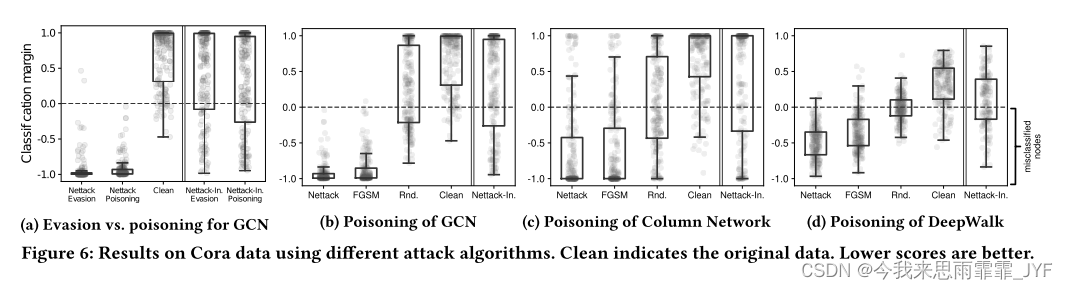
在这里插入图片描述
图 6b 和 6c 显示 Nettack 生成的损坏转移到不同的（半监督）图卷积方法：GCN [20] 和 CLN [29]。最值得注意的是，即使是无监督模型 DeepWalk [28] 也会受到我们的扰动的强烈影响（图 6d）。由于DW只处理无属性图，因此只进行结构攻击。按照[28]，通过对学习到的嵌入训练逻辑回归来执行节点分类。总的来说，我们发现直接攻击比影响者攻击更困难。在这些图中，我们还与两个基线 Rnd 和 FGSM 进行比较，两者都在直接攻击设置中运行。如图所示，Nettack 的性能优于两者。再次注意：所有这些结果都是通过具有挑战性的中毒攻击（即模型的重新训练）获得的。
在表 3 中，我们总结了不同数据集和分类模型的结果。在这里，我们报告被正确分类的目标节点的比例。我们对代理模型的对抗性扰动可以转移到我们评估的所有三个模型和所有数据集上。毫不奇怪，与直接攻击相比，影响者攻击导致的性能下降幅度较小。
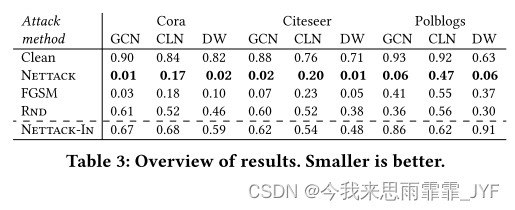
在这里插入图片描述
我们发现 FGSM 的性能比 Nettack 差，我们认为这是因为梯度方法对于离散数据不是最佳的。图 4 显示了为什么会出现这种情况：我们绘制了改变 𝐴 中的元素时梯度与实际损失变化的关系。通常，梯度不能很好地近似损失——在（b）和（c）中，甚至符号也不匹配。Nettack 的一个关键优势是我们可以精确有效地计算 L𝑠 的变化。

知识有限

在之前的实验中，我们假设完全了解输入图，这是最坏情况攻击的合理假设。在图 7 中，我们在知识有限的情况下分析结果：给定目标节点 𝑣0，我们仅向模型提供相对于 Cora 图的大小而言尺寸不断增加的子图。我们通过选择与 𝑣0 距离不断增加的节点来构建这些子图，即我们首先选择 1 跳邻居，然后选择 2 跳邻居，依此类推，直到达到所需的图大小。然后，我们使用本文提出的攻击策略扰动子图。然后将这些扰动转移到完整的图表中，我们在其中训练 GCN。请注意，Nettack 始终只看到子图；而它的代理模型也只是基于它来训练的。
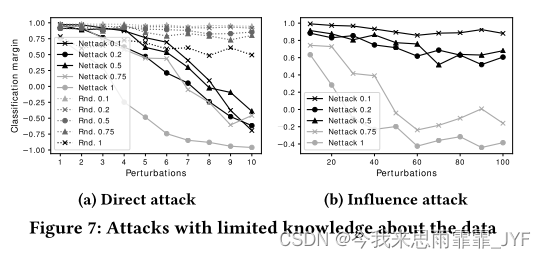
在这里插入图片描述
图 7 显示了直接攻击的结果。正如所见，即使只观察到图表的 10%，我们仍然可以对其进行显着攻击。显然，如果攻击者知道完整的图，则需要最少数量的扰动。为了进行比较，我们包括 Rnd 攻击，它也只在子图上运行。在图 7 中我们看到了影响攻击。在这里，我们需要更多的扰动和 75% 的图大小才能使我们的攻击成功。尽管如此，这个实验表明并不需要完整的知识。

结论

我们提出了第一个关于图的对抗性攻击的工作，特别关注通过图卷积网络进行节点分类的任务。我们的攻击针对节点的特征和图结构。利用数据的关系性质，我们提出了直接攻击和影响攻击。为了确保即使在离散的关系域中也不会发生明显的变化，我们建议保留图的度分布和特征共现。我们开发的算法可以在离散域中实现有效的扰动。根据我们广泛的实验，我们可以得出结论，即使是具有挑战性的中毒攻击也可以通过我们的方法成功。即使只有部分图表知识可用或攻击仅限于少数影响者，分类性能也会持续降低。更重要的是，这些攻击可以推广到其他节点分类模型。
研究图深度学习模型的鲁棒性是一个重要问题，这项工作为更深入的研究提供了重要的见解。作为未来的工作，我们的目标是对现有模型进行扩展，以变得更强大，能够抵御攻击，并且我们的目标是研究节点分类之外的任务。