代码随想录算法训练营第五十六天 | LeetCode 647. 回文子串、516. 最长回文子序列、动态规划总结

news2024/11/26 11:53:52

代码随想录算法训练营第五十六天 | LeetCode 647. 回文子串、516. 最长回文子序列、动态规划总结

文章链接：回文子串、最长回文子序列、动态规划总结
视频链接：回文子串、最长回文子序列

1. LeetCode 647. 回文子串

1.1 思路

本题是给个字符串 s 求里面有多少个回文子串，单独一个元素也是回文子串
dp 数组及其下标的含义：本题如果以 dp[i] 为下标 i 为结尾的字符串有 dp[i] 个回文串的话很难发现递推关系，很难看出和 dp[i-1] 或者 dp[i+1] 有什么关系。我们判断一个长度为 5 的元素时，如果范围 [1,3] 已经是回文的了，那么我们再判断 0 和 4 下标是否为回文就是了，也就是判断一个范围 [i,j] 是否为回文子串依赖于范围 [i+1,j-1] 是否为回文子串。因此定义二维数组 dp[i][j] 表示区间左闭右闭 [i,j] 是否为回文子串，是的话为 true，否则为 false。并且定义个变量 result 记录有多少个回文子串
递推公式：根据 dp 数组，我们判断两边的元素是否相同，如果相同就可以重复依赖于中间计算过的结果，i 是<=j 的，if（s[i]s[j]）情况 1，ij，指向的是同一个元素，只有一个元素作为子串，比如 a，那这个也是回文子串；情况 2：i 和 j 相差 1，也就是相邻的，就是两个元素，比如 aa，那这个也是回文子串；情况 3：j-i>1，之间有很多元素，就要看 i+1 和 j-1 是否为回文子串，也就是依赖 dp[i+1][j-1] 是否为 true，如果是，那么这一段也是回文子串。if（j-i<=1）dp[i][j]=true，result++，这里就是情况 1 和 2；else if（dp[i+1][j-1]==true）dp[i][j]=true，result++，这里就是情况 3。这里为什么不讨论 s[i]!=s[j] 的情况呢？不相同就是默认 false 咯
dp 数组的初始化：我们定义的是布尔类型的 dp 数组，默认全为 false 即可，为 true 就错了

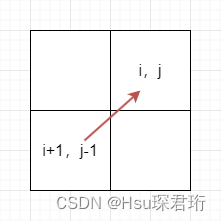
在这里插入图片描述
5. 遍历顺序：根据递推公式得到推导方向，我们计算 dp[i][j] 时是需要 dp[i+1][j-1] 的值，因此遍历顺序要从下往上从左往右。for（int i=s.length()-1；i>=0；i–）for（int j=i；j<s.length()；j++）j 为什么从 i 后面开始，因为我们的递推公式中 j 一定比 i 大。最终结果是 result
6. 打印 dp 数组：用于 debug
7. 双指针：本题也可以用双指针，一个指向中心，另一个向两边扩散，判断是否为回文子串

1.2 代码

class Solution {
    public int countSubstrings(String s) {
        char[] chars = s.toCharArray();
        int len = chars.length;
        boolean[][] dp = new boolean[len][len];
        int result = 0;
        for (int i = len - 1; i >= 0; i--) {
            for (int j = i; j < len; j++) {
                if (chars[i] == chars[j]) {
                    if (j - i <= 1) { // 情况一 和 情况二
                        result++;
                        dp[i][j] = true;
                    } else if (dp[i + 1][j - 1]) { //情况三
                        result++;
                        dp[i][j] = true;
                    }
                }
            }
        }
        return result;
    }
}

2. LeetCode 516. 最长回文子序列

2.1 思路

本题是给一个字符串求一个最长的回文子序列的长度，注意是子序列，也就是不要求连续的，在647. 回文子串中是子串，要求连续，比方说本题里“bbbab”的最长回文子序列是“bbbb”，长度是 4。
dp 数组及其下标的含义：在647. 回文子串中讲解过为什么要利用二维数组，判断 [i,j] 范围是否为回文子串是要依赖于 [i+1,j-1]。dp[i][j] 表示 [i,j] 的回文子序列的长度为 dp[i][j]
递推公式：if（s[i]==s[j]）dp[i][j]，先看看里面的范围也就是 [i+1,j-1] 范围内的最长回文子序列的长度就是 dp[i+1][j-1]，因此 dp[i][j] 就是在这基础上+2。如果不相同 else 就不能同时把两个元素加进来了，就要分别考虑两个元素，先考虑 s[i]，如果加入里面的范围里，就变为了 [i,j-1] 的最长回文子序列的长度就是 dp[i,j-1]，如果考虑 s[j]，那就是变为了 [i+1,j] 的最长回文子序列的长度就是 dp[i+1,j]，因此 dp[i][j]=Math.max（dp[i,j-1]，dp[i+1,j]）
dp 数组的初始化：i 是一直+1 往中间移动，j 是一直-1 往中间移动，一直移动到最中间的位置，也就是 ij 指向同一个元素，这个情况是递推公式没有考虑到的，需要初始化的，指向同一个元素的最长回文子序列长度就是 1 了，即 dp[i][i]=1，这里写成两个 i 是为了体现相同位置，也就是 ij 的情况就初始化为 1 即可。for（int i=0;i<s.length()；i++）dp[i][i]=1
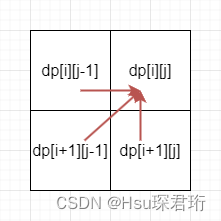
遍历顺序：根据递推公式得到推导方向，因此我们的遍历方向是从下往上从左往右，for（int i=s.length()；i>=0；i–）for（int j=i+1；j<s.length()；j++）j 为什么从 i 后面开始，因为我们的递推公式中 j 一定比 i 大；j 为什么要比 i 大 1 啊，因为 j==i 的情况初始化时已经处理过了，直接从 i+1 开始。这里两层 for 循环可以颠倒吗？不可以，因为 j 是依赖于 i 的，j 一定大于等于 i 的，颠倒了就控制不了 j>=i 了，因此要先明确了 i 的范围才能明确 j 的范围。最终结果是在 dp[0][s.length()-1] 也就是右上方的位置
打印 dp 数组：用于 debug

2.2 代码

public class Solution {
    public int longestPalindromeSubseq(String s) {
        int len = s.length();
        int[][] dp = new int[len + 1][len + 1];
        for (int i = len - 1; i >= 0; i--) { // 从后往前遍历 保证情况不漏
            dp[i][i] = 1; // 初始化
            for (int j = i + 1; j < len; j++) {
                if (s.charAt(i) == s.charAt(j)) {
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                } else {
                    dp[i][j] = Math.max(dp[i + 1][j], Math.max(dp[i][j], dp[i][j - 1]));
                }
            }
        }
        return dp[0][len - 1];
    }
}