一、理论
计算置信区间的具体方法通常取决于所选择的统计分布以及所使用的估计方法。在正态分布下,以样本均值为中心的置信区间的计算是比较常见的,尤其是当样本大小足够大时,根据中心极限定理,样本均值的分布接近正态分布。
以下是计算正态分布下置信区间的一般步骤:

- 计算标准误差(Standard Error,SE):
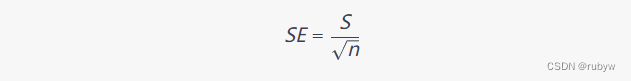
-
查找临界值: 使用标准正态分布的临界值,可以在正态分布的 z 表或使用统计软件进行查找。对于双侧置信区间,我们通常查找两侧面积各为 α/2的临界值。

-
计算置信区间:

例如
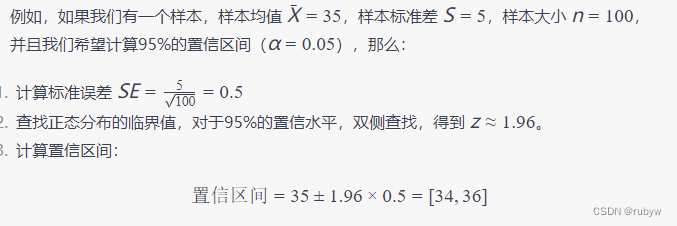
这表示我们有95%的信心认为总体均值落在34到36之间。需要注意,这个方法假设样本来自正态分布,如果样本不服从正态分布,而样本大小又较小,可能需要使用 t 分布进行估计。
二、置信水平
置信水平是用来表示对一个估计值的信心程度的概念,通常以百分比的形式表示。常见的置信水平包括:
-
90%置信水平: 表示我们有90%的信心认为真实的参数值位于计算出的置信区间内。
-
95%置信水平: 这是最常见的置信水平之一,表示我们有95%的信心认为真实的参数值位于计算出的置信区间内。
-
99%置信水平: 表示我们有99%的信心认为真实的参数值位于计算出的置信区间内。这个置信水平更高,对于一些要求较高置信度的研究或决策可能会选择使用。
这些置信水平通常与统计推断中的置信区间概念一起使用。当我们进行参数估计时,我们不仅仅给出一个点估计值,还会提供一个置信区间,以便于对真实值的不确定性有一个更好的理解。选择置信水平时,需要在准确性和置信度之间进行权衡。更高的置信水平通常意味着更宽的置信区间,因为我们需要更加谨慎地估计真实值的范围。
三、显著性水平α
在统计学中,显著性水平(significance level)通常用符号 (\alpha) 表示,它表示在进行假设检验时拒绝原假设的概率。常见的显著性水平包括:
-
α = 0.05): 这是最常见的显著性水平之一,通常用于很多统计假设检验中。它表示在5%的显著性水平下,我们会拒绝原假设。
-
α = 0.01): 这是一个较为严格的显著性水平,用于一些对精度要求较高的研究中。它表示在1%的显著性水平下,我们会拒绝原假设。
-
α = 0.10): 这是一个相对较宽松的显著性水平,有时在一些初步研究中使用。它表示在10%的显著性水平下,我们会拒绝原假设。
显著性水平的选择需要根据研究的具体背景、数据的性质以及研究者对错误类型的容忍度进行权衡。通常,选择一个适当的显著性水平是研究设计中的一个关键步骤,因为它直接影响到实验或调查结果的解释和结论。
四、临界值
临界值是在假设检验中用于判断是否拒绝原假设的关键值。它们与显著性水平α和检验的自由度有关。在不同的假设检验和分布假设下,临界值的计算方式可能会有所不同。以下是一些常见情况下的临界值:
-
正态分布的临界值:
- 对于双侧检验,通常使用正态分布的 z 分布。
- 在 α = 0.05 水平下,双侧检验的临界值约为 ±1.96。
- 在 α = 0.01 水平下,双侧检验的临界值约为 ±2.58。
- 对于单侧检验,将双侧检验的临界值调整,例如,在 (\alpha = 0.05) 水平下,单侧检验的临界值为 ±1.645。
- 对于双侧检验,通常使用正态分布的 z 分布。
-
t 分布的临界值:
- 当样本容量较小,或总体标准差未知时,通常使用 t 分布。
- t 分布的临界值取决于自由度和显著性水平。
- 例如,在 α = 0.05 水平下,自由度为 df 的 t 分布的双侧检验的临界值可通过查找 t 分布表或使用统计软件来获取。
-
卡方分布的临界值:
- 用于卡方检验。
- 卡方分布的临界值取决于自由度和显著性水平。
- 例如,在α = 0.05 水平下,自由度为 df 的卡方分布的双侧检验的临界值可通过查找卡方分布表或使用统计软件来获取。
具体的临界值需要根据具体的假设检验和问题情境进行计算或查找。在实际应用中,统计软件通常提供了方便的方法来获取临界值。