JAVA代码编写
235. 二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
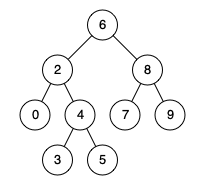
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉搜索树中。
教程:https://programmercarl.com/0235.%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E7%9A%84%E6%9C%80%E8%BF%91%E5%85%AC%E5%85%B1%E7%A5%96%E5%85%88.html
视频:https://www.bilibili.com/video/BV1jd4y1B7E2
方法一:递归
思路:根结点的值都大于p和q的值,就继续在左子树中递归,否则就右子树中继续递归。
复杂度分析:
- 时间复杂度: O(n),其中n是二叉树中节点的个数
- 空间复杂度:
- 在递归调用的过程中,在最坏情况下是O(n)
- 在平衡的二叉搜索树中,递归的层数通常为log(n)
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root.val > p.val && root.val > q.val) return lowestCommonAncestor(root.left, p, q);
if (root.val < p.val && root.val < q.val) return lowestCommonAncestor(root.right, p, q);
return root;
}
}
701. 二叉搜索树中的插入操作
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
示例 1:
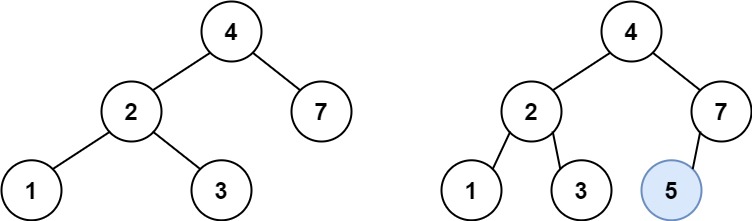
输入:root = [4,2,7,1,3], val = 5
输出:[4,2,7,1,3,5]
解释:另一个满足题目要求可以通过的树是:
示例 2:
输入:root = [40,20,60,10,30,50,70], val = 25
输出:[40,20,60,10,30,50,70,null,null,25]
示例 3:
输入:root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出:[4,2,7,1,3,5]
提示:
- 树中的节点数将在
[0, 104]的范围内。 -108 <= Node.val <= 108- 所有值
Node.val是 独一无二 的。 -108 <= val <= 108- 保证
val在原始BST中不存在。
教程:https://programmercarl.com/0701.%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E4%B8%AD%E7%9A%84%E6%8F%92%E5%85%A5%E6%93%8D%E4%BD%9C.html#%E7%AE%97%E6%B3%95%E5%85%AC%E5%BC%80%E8%AF%BE
视频:https://www.bilibili.com/video/BV1Et4y1c78Y/
方法一:递归
思路:
复杂度分析:
- 时间复杂度: O(h),其中h是二叉搜索树的高度,最坏情况下为O(n),其中n是树中节点的数量。
- 空间复杂度: O(1)
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
if (root == null) return new TreeNode(val);
TreeNode newRoot = root;
TreeNode pre = root;
while (root != null) {
pre = root;
if (root.val > val) {
root = root.left;
} else if (root.val < val) {
root = root.right;
}
}
if (pre.val > val) {
pre.left = new TreeNode(val);
} else {
pre.right = new TreeNode(val);
}
return newRoot;
}
}
450. 删除二叉搜索树中的节点
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
- 首先找到需要删除的节点;
- 如果找到了,删除它。
示例 1:

输入:root = [5,3,6,2,4,null,7], key = 3
输出:[5,4,6,2,null,null,7]
解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
示例 3:
输入: root = [], key = 0
输出: []
提示:
- 节点数的范围
[0, 104]. -105 <= Node.val <= 105- 节点值唯一
root是合法的二叉搜索树-105 <= key <= 105
进阶: 要求算法时间复杂度为 O(h),h 为树的高度。
教程:https://programmercarl.com/0450.%E5%88%A0%E9%99%A4%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E4%B8%AD%E7%9A%84%E8%8A%82%E7%82%B9.html
视频:https://www.bilibili.com/video/BV1tP41177us/
方法一:递归
思路:
复杂度分析:
- 时间复杂度: O(h),其中h是二叉搜索树的高度,最坏情况是O(n)
- 空间复杂度: O(n),n是树的节点数量
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if (root == null) return root;
if (root.val == key) {
if (root.left == null) {
return root.right;
} else if (root.right == null) {
return root.left;
} else {
TreeNode cur = root.right;
while (cur.left != null) {
cur = cur.left;
}
cur.left = root.left;
root = root.right;
return root;
}
}
if (root.val > key) root.left = deleteNode(root.left, key);
if (root.val < key) root.right = deleteNode(root.right, key);
return root;
}
}