一.层次分析法的定义
层次分析法，简称AHP，是指将与决策总是有关的元素分解成目标、准则、方案等层次，在此基础之上进行定性和定量分析的决策方法，是一种层次权重决策分析方法。
层次分析法是一种主观赋值评价方法，也是一个多指标综合评价算法，常用于综合评价类模型。
是在分析一个现象或问题之前，首先将现象或问题根据他们的性质分解为相关因素，并依据因素之间的关系形成一个多层次的结构模型。然后通过经验或专家来判断低层元素对高层元素的相对重要性，并根据重要性的程度得出权重排序。
二.评价类问题
评价类问题从以下三个方面出发：
（1）我们评价的目标是什么？
（2）为了达到这个目标有几种可以选择的方案？
（3）评价的准则或者说指标是什么？
三.如何解决权重问题
问题：
一次性考虑多个指标问题，往往考虑不够周全
解决方法：
两个两个进行考虑，最终根据两两比较的结果推算出权重。
四.重要性表
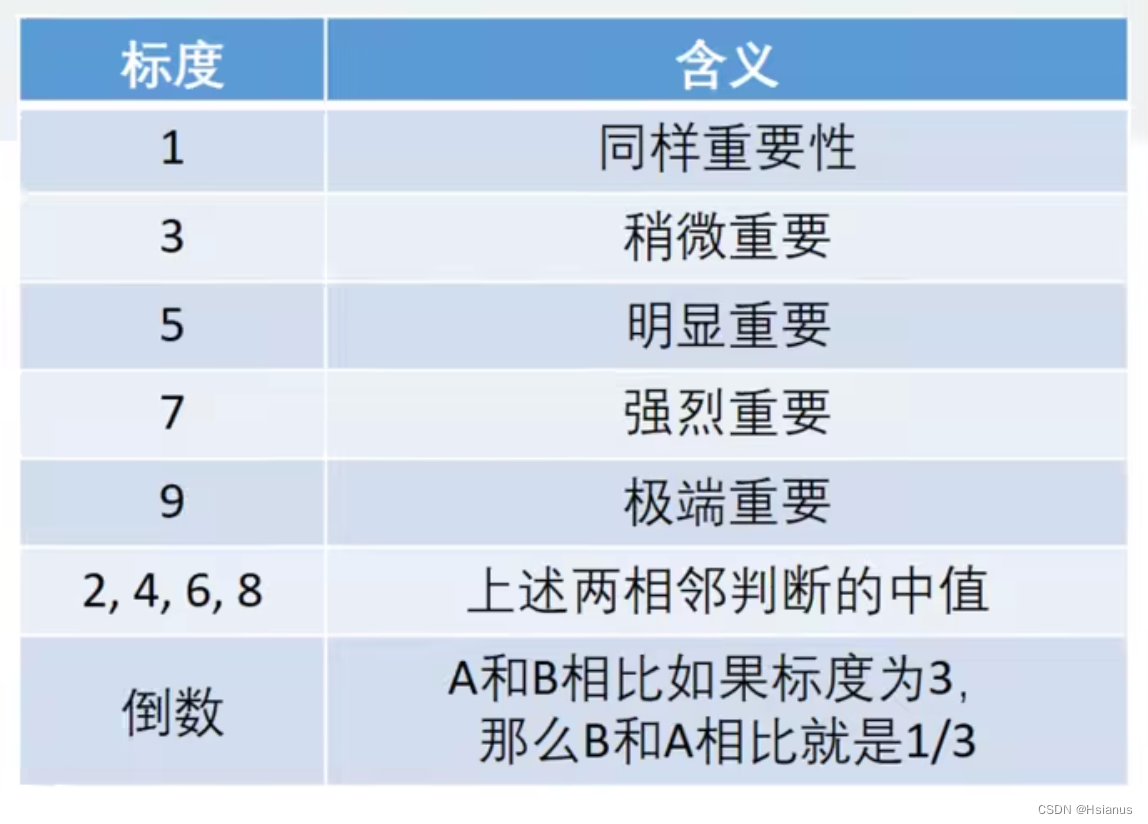
五.根据重要性表导出判断矩阵
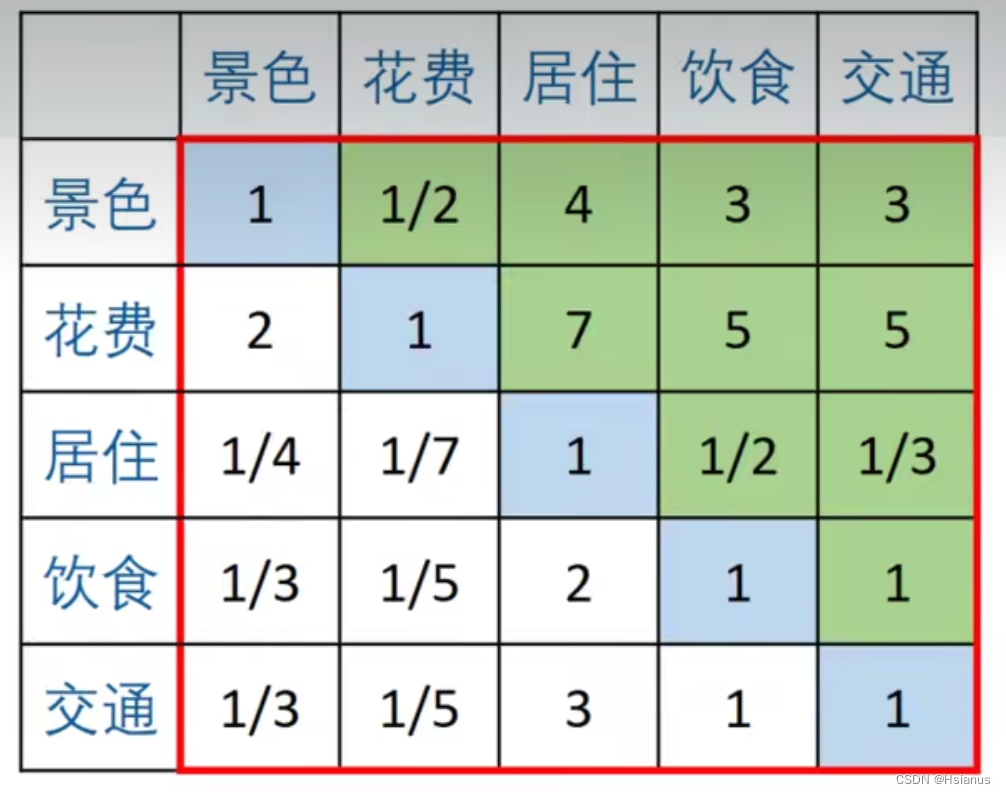
矩阵的特点：
（1）aij代表：与指标j相比i的重要程度
（2）当i=j时，两个指标相同，同等重要记为1
（3）aij * aji=1 称此矩阵为正互反矩阵
六.一致矩阵
若正互反矩阵满足 aij * ajk=aik，则我们称之为正互反矩阵。
各行（列）成倍数关系
在使用判断矩阵求权重之前，必须对其进行一致性检查。
七.一致性检验
定义：检验构造矩阵与一致矩阵是否有太大差别
当矩阵为一致矩阵时，矩阵的秩为1
有一个特征值为n（对角线元素相加是矩阵的迹），其余特征值均为0
引理：n阶正互反矩阵为一致矩阵当且仅当最大特征值为n
而n阶正互反矩阵不为一致矩阵，最大特征值一定大于n
判断矩阵与一致矩阵差别越大，最大特征值与n相差越大。
一致性检验的步骤：
1）计算一致性指标CI
CI=（max-n）/n-1
2）查找对应的平均随机一致性指标值RI
3）计算一致性比例
CR=CR/RI
说明：如果CR<0.1 则判断矩阵的一致性可以接受，否则需要修正
八.一致矩阵怎么计算权重
使用归一化处理
例如：
一致矩阵
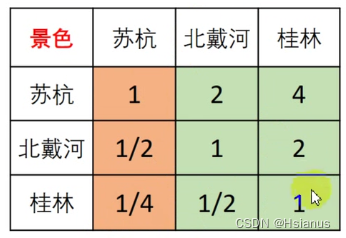
苏杭：1/（1+1/2+1/4）
北戴河：（1/2）/（1+1/2+1/4）
判断矩阵：
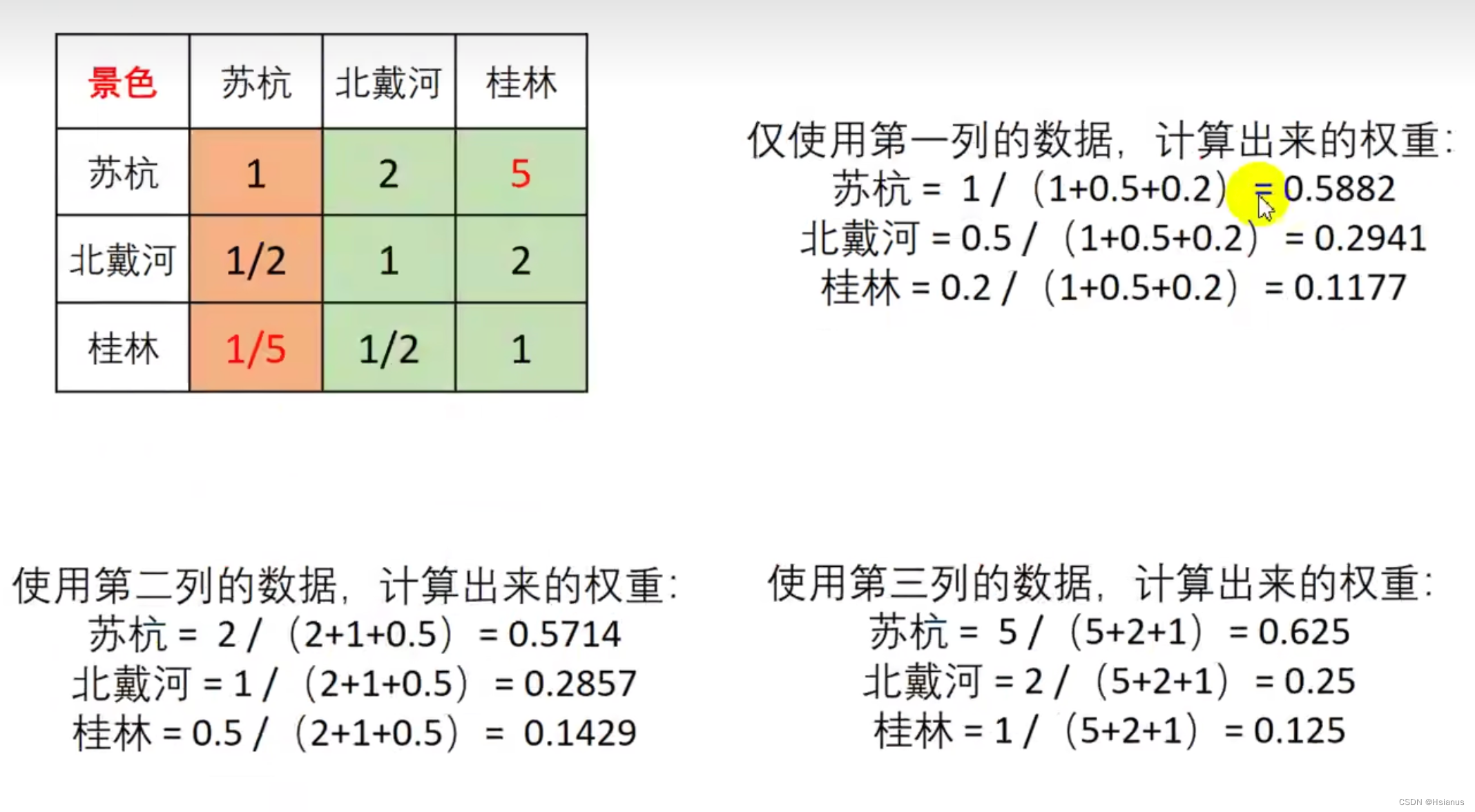
（1）算数平均法求权重：
1）将判断矩阵按照列进行归一化处理。
2）归一化的各列，按列求和。
3）每个向量除以n，得到权重。
（2）几何平均法求权重
1）将矩阵的元素按照行相乘得到新的列向量
2）将新的列向量每个分量开n次方
3）对列向量进行归一化
（3）特征值法求权重
对于一致矩阵，只有一个特征值为n，其余均为0.
对于这个值为n的特征值，其对应的特征向量为第一列的向量。
而对于判断矩阵，采用类似的方法。
首先，根据最大特征值，找到对应的特征向量。
然后，对于求出的特征向量，进行一致化处理。
九.利用EXCEL快速进行运算
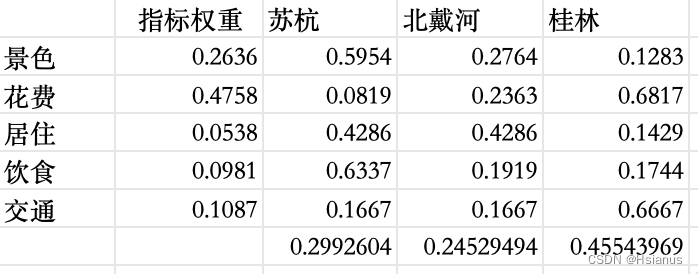fn+f4 可以锁定单元格
十.总结
1.分析系统中各因素之间的关系，建立系统的递阶层次结构。
目标，准则，方案。
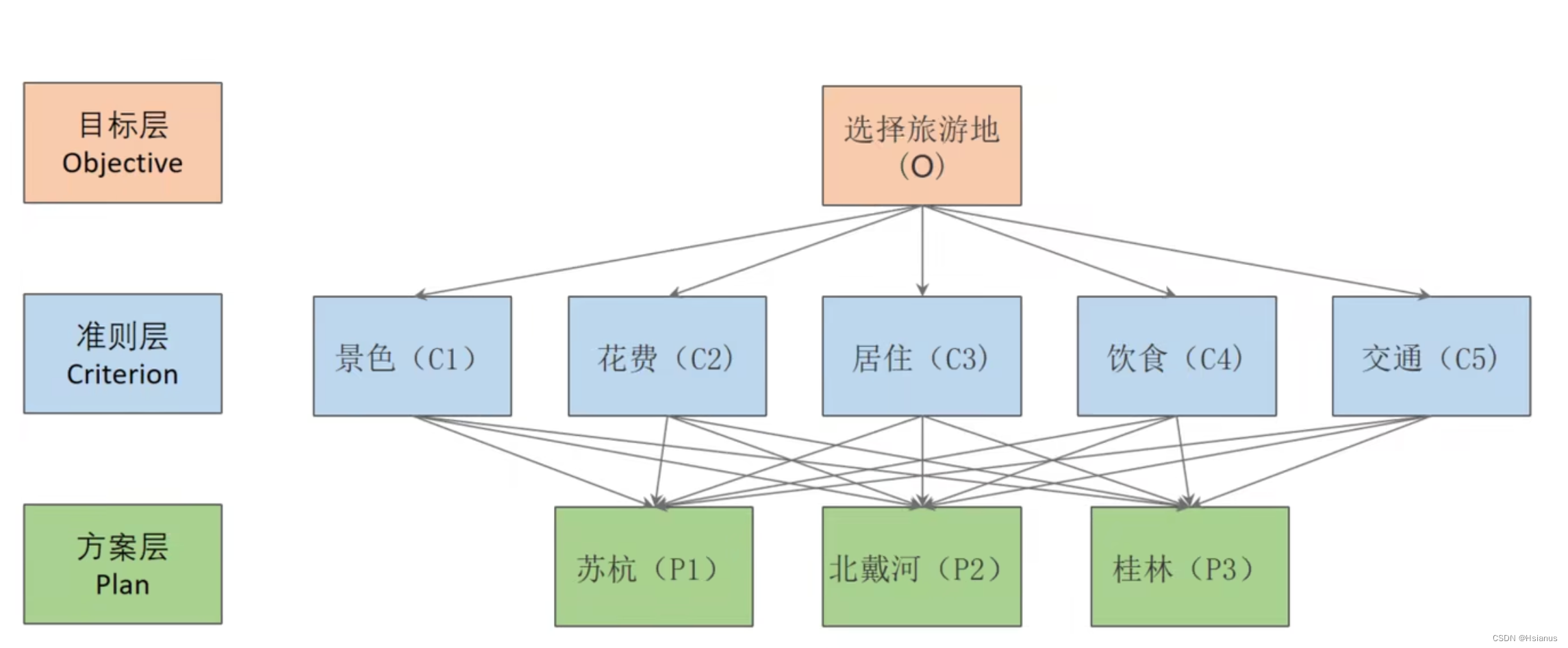
层次结构图的构建
判断矩阵的生成：
搜集资料生成判断矩阵
层次分析法的局限性：
评价的决策层不能太多
