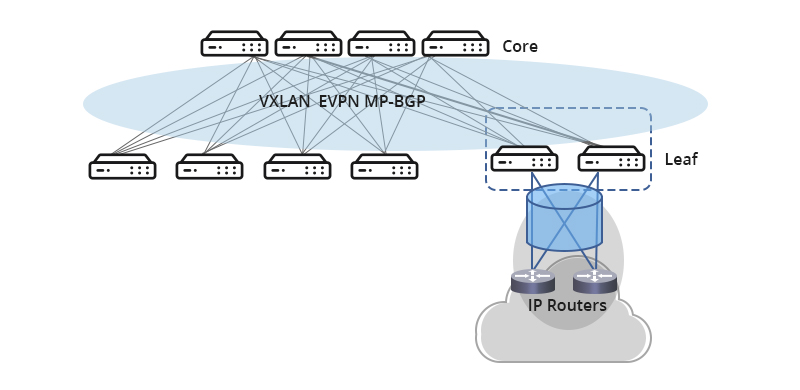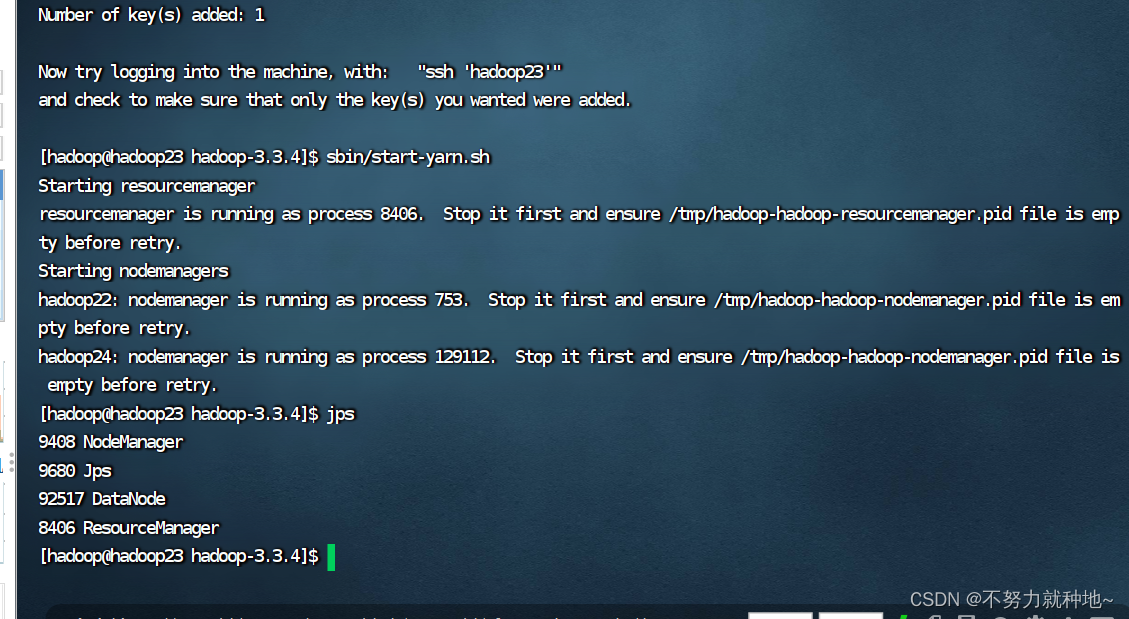
• 机器数：一个数在计算机中的二进制表示形式，称为这个数的机器数。
• 符号位：机器数是带符号的，在计算机中用最高位作为符号位，0为正数，1为负数。
• 真值：机器数由于含有符号位，所以机器数的值并不等于真实值。将带符号位的机器数所对应的真实数值称为机器数的真值。
• 为便于计算，带符号的机器数可采用原码、反码、补码、移码等不同编码方式。
• 原码：是最简单的机器数表示法，用最高位表示符号，其余位表示该数的二进制绝对值。
• 反码：正数的反码是其本身，负数的反码是符号位不变，其余位取反。（在反码中，数值0有两种表示方法）（原码最大的问题就在于一个数加上它的相反数不等于0，反码的设计思想就是为了解决这个问题，既然一个负数是一个正数的相反数，那干脆用一个正数按位取反来表示负数）

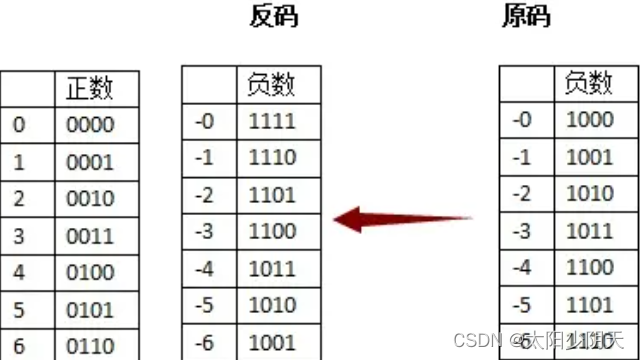
此时，再试着用反码的方式解决一下源码的问题：0000 0001 + 1111 1110 = 1111 1111，即1+（-1）= -0 结果正确；1111 1110 + 1111 1100 = 1111 1010，（-1）+（-3）= -5，结果错误。两个相反数相加等于0，但是两个负数相加结果不对。

• 补码：正数的补码是其本身，负数的补码是其反码+1。（这只是求法，并不是补码定义）
• 移码：不管正负数，只要将其补码的符号位取反即可。
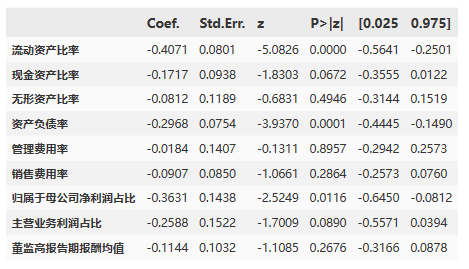
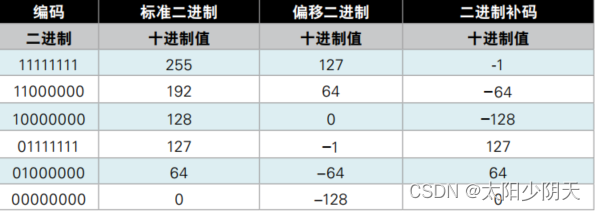
• 八位二进制数0000 0000 ~ 1111 1111 共个数，如果无符号整数可表示0~255。如果是有符号整数，第一位二进制位为符号位，其余位为数值域。
• 在原码中，0的表示有两种（+0）0000 0000和（-0）1000 0000，这样就产生了编码映射的不唯一性，在计算机上就要去区分，然而+0和-0并没有现实意义。
• 为解决上述数的表示问题，我们强制把转换后的1000 0000认定为-128，但这又出现了一个新的问题，即数的运算。
• 为解决上述数的运算问题，进行如下思考：在数学上，1+（-1）=0，而在二进制中，0000 0001 + 1000 0001=1000 0010，换算成十进制为-2，显然是错了。所以原码符号位不能直接参与运算，必须和其他位分开，但这增加了硬件的开销和复杂性。这个时候就要引入补码。为何引入补码？负数补码定义为何是相应的正数原码取反加一？
• 为何引入补码？是为了解决计算机中数的表示和数的运算问题，使用补码，可以将符号位和数值域统一处理，即引用了模运算在数理上对符号位的自动处理，利用模的自动丢弃，实现了符号位的自然处理，仅仅通过编码的改变就可以在不更改机器物理架构的基础上完成预期要求。
• 为何取反加一？模的概念可以帮助理解补数和补码。“模”指的是一个计量系统的计量范围。如时钟的计量范围是0~11，模=12；n位计算机的计量范围是0~，模=。“模”实质上是计量器产生“溢出”的量，它的值在计量器上表示不出来，计量器上只能表示出模的余数。任何有模的计量器，均可化减法运算为加法运算。例如：当前时针指向10点，而准确时间是6点，调整时间有以下两种拨法：一种是倒拨4个小时，即10-4=6；另一种是顺拨8小时，即10+8=12+6。在以12为模的系统中，加8和减4的效果是一样的，因此可以化减法运算为加法运算。对“模”而言，8和4互为补数。在以12为模的系统中，11和1，10和2，9和3，7和5, 6和6都有这个特性，共同特点是两者之和等于模。对于计算机而言，其概念和方法完全一样，n位计算机，假设n=8，不讨论符号位，则所能表示最大的数是1111 1111，若再加1，成为10000 0000，但因为只能有8位，最高位1自然丢失。又回到了0000 0000，所以8位二进制系统的模为。在这样的系统中，减法运算也可化为加法运算，只需把减数用相应的补数表示就可以，把补数用到计算机对数的处理上，就是补码。
• 正数的补码表示就是其本身，负数的补码表示的实质是把负数映像到正值区域，因此加上一个负数或减去一个正数，可以用加上另一个数（负数或减数对应的补码）来代替。从补码表示的符号看，补码中符号位的值代表了数的正确符号，0表示正数，1表示负数；而从映像值来看，符号位的值是映像值的一个数位，因此在补码运算中，符号位可以与数值位一起参加运算。

• 八位二进制数表示范围为-128~+127。

举例：

不考虑符号位：

0110-0010，6-2=4，但是由于计算机中没有减法器，没法算。这时候，想想时钟运算中，减去一个数，是可以等同于加上另外一个正数（同余数），这个数与减数相加正好等于模。也就是四位二进制数最大容量是多少？其实就是2^4=16（10000）。那么-2的同余数，就等于10000-0010=1110，16-2=14。既然如此，0110-0010=0110+1110=10100，6-2=6+14=20。按照这种算法得出的结果是10100，但是对于四位二进制数最大只能存放4位，如果低四位正好是0100，正好是想要的结果，至于最高位的1，计算机会把它放入psw寄存器进位位中，8位机会放在cy中，x86会放在cf中，这里不做讨论。此时，再想想在四位二进制数中，减去2就相当于加上它的同余数（至于它们为什么同余，建议看《计算机组成原理》）。但是减去2，从另一个角度来说，也是加上-2，即加上-2和加上14得到的二进制结果除了进位位，结果是一样的。如果我们把1110的最高位看作符号位后就是-2的补码，这可能也是为什么负数的符号位是1，而不是0。

       

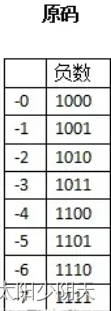
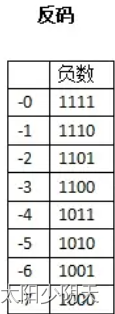
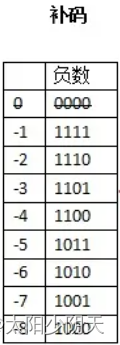
在补码中也不存在-0了，因为1000表示-8。

参考文献：（强烈推荐第一个引用文献）

(5 封私信) 为什么-8对应的原码、补码是1000，反码是1111? - 知乎 (zhihu.com)

《 模拟工程师口袋书》

二进制的原码、反码、补码 - 知乎 (zhihu.com)

八位二进制数能表示数的范围以及原码、反码和补码含义_8位2进制-CSDN博客