文章目录
- 1 概念
- 2 Kosaraju算法
- 2.1 在图类中设计反图
- 2.2 强连通分量的判断和普通联通分量的区别
- 2.3 代码实现
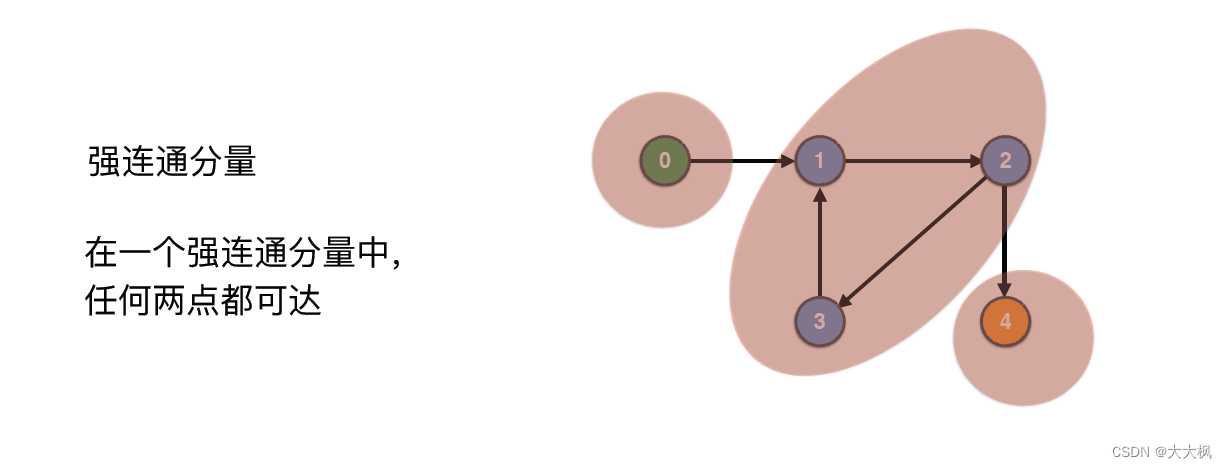
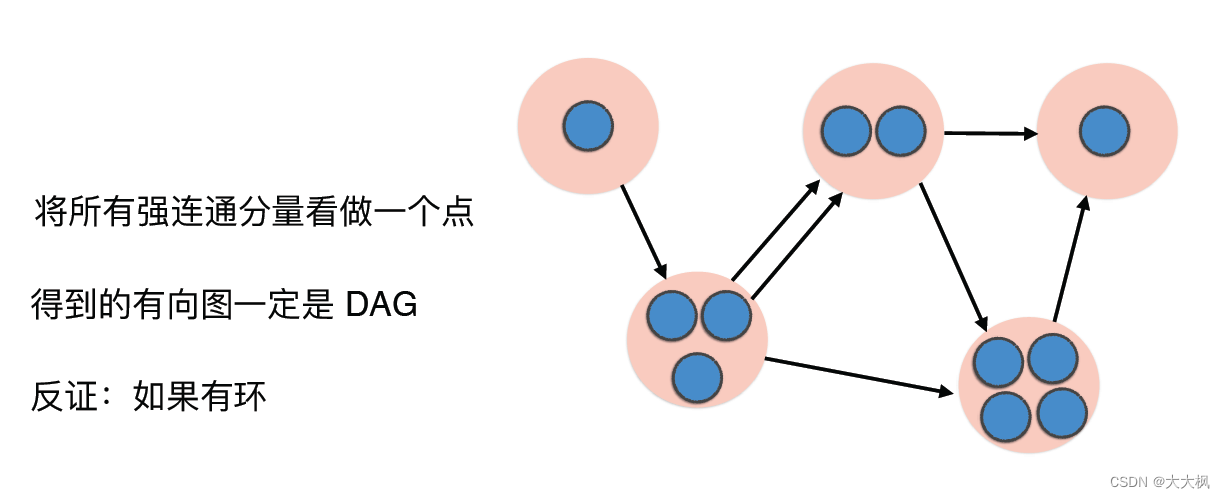
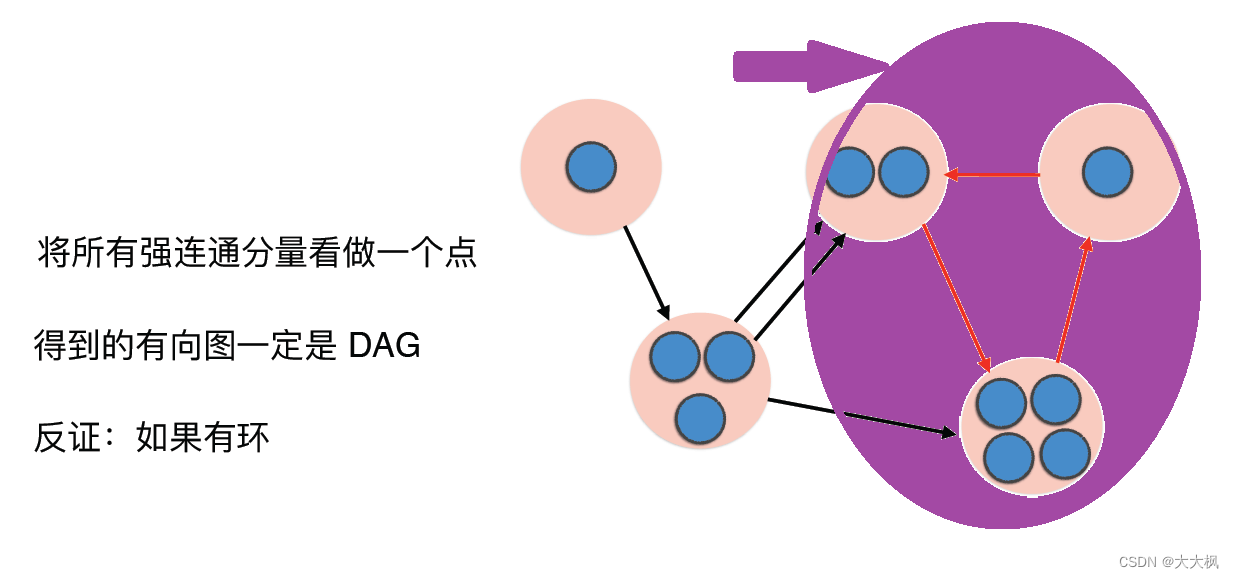
1 概念
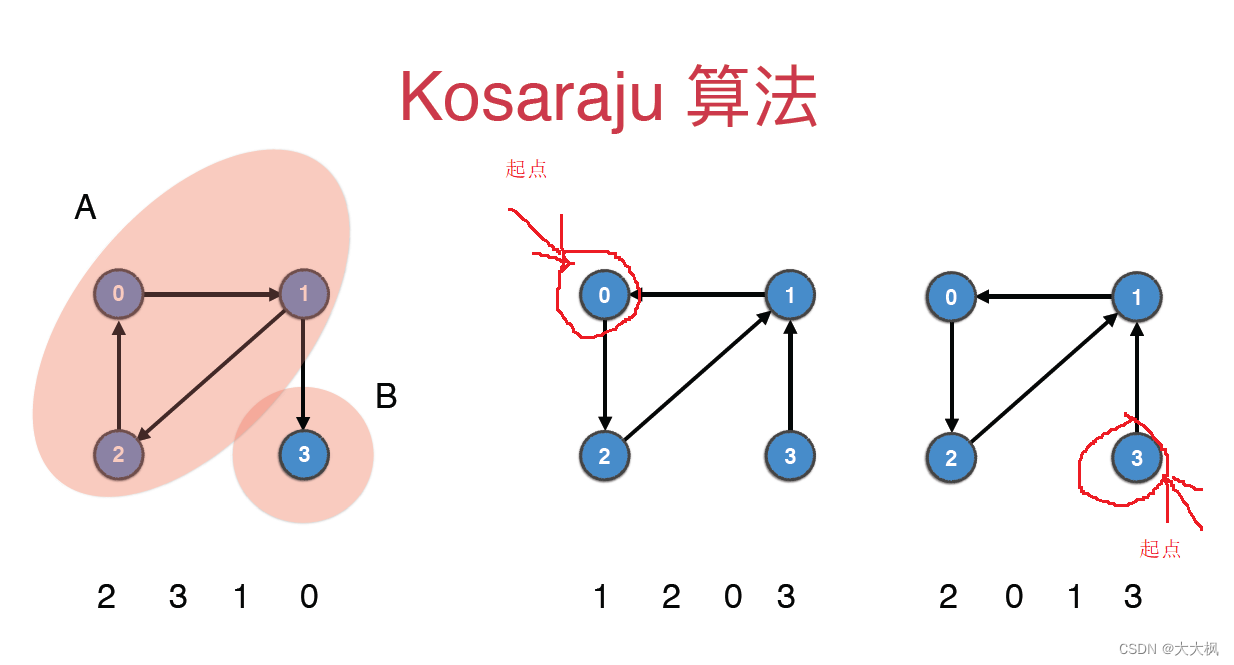
2 Kosaraju算法
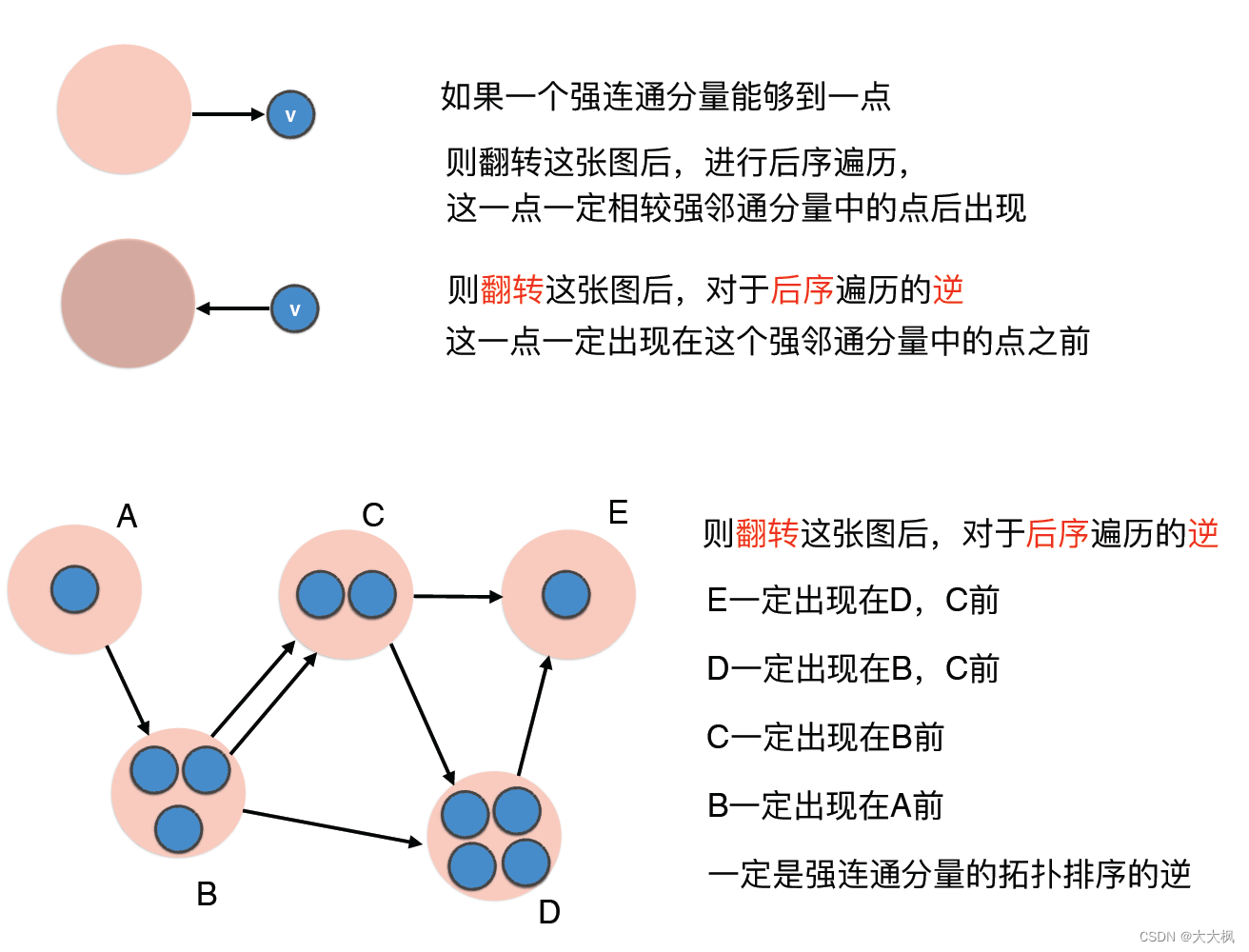
对原图的反图进行DFS的后序遍历。
2.1 在图类中设计反图
// 重写图的构造函数
public Graph(TreeSet<Integer>[] adj, boolean directed){
this.adj = adj;
this.directed = directed;
this.V = adj.length;
this.E = 0;
indegrees = new int[V];
outdegrees = new int[V];
for(int v = 0; v < V; v ++)
for(int w: adj[v]){
outdegrees[v] ++;
indegrees[w] ++;
this.E ++;
}
if(!directed) this.E /= 2;
}
// 求反图,并且new一个图对象,参数为TreeSet
public Graph reverseGraph(){
TreeSet<Integer>[] rAdj = new TreeSet[V];
for(int i = 0; i < V; i ++)
rAdj[i] = new TreeSet<Integer>();
for(int v = 0; v < V; v ++)
for(int w : adj(v))
rAdj[w].add(v);
return new Graph(rAdj, directed);
}
2.2 强连通分量的判断和普通联通分量的区别
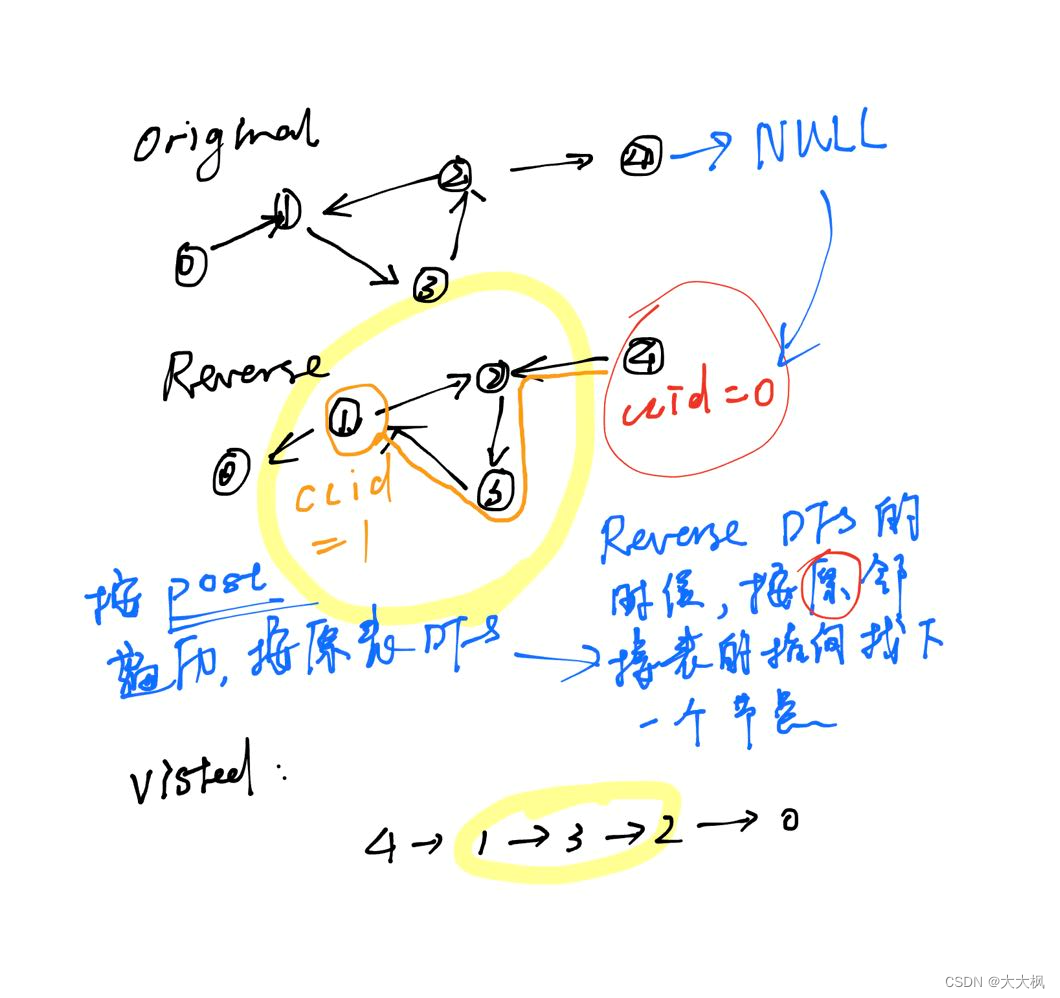
强联通分量是环,意味着在DFS过程中一定是公用相同的联通分量序号。
当这个环遍历从环尾开始返回并记录ccid的时候,DFS自由返回到环, 索引指向下一个未被访问过的环外的节点,此时联通分量序号+1。 由于图是反过来的。
单步调试一下更容易理解。
2.3 代码实现
顶点:注意这里遍历的顺序是反过来的图。
并且,对翻转过来的图进行DFS后序遍历。
GraphDFS dfs = new GraphDFS(G.reverseGraph());
ArrayList<Integer> order = new ArrayList<>();
for(int v: dfs.post())
order.add(v);
Collections.reverse(order);
for(int v: order) //注意这里遍历的顺序是反过来的图
if(visited[v] == -1){
dfs(v, scccount);
scccount ++;
}
但是在DFS的时候,判断邻边用的是原来的邻接列表。
private void dfs(int v, int sccid){
visited[v] = sccid;
for(int w: G.adj(v))
if(visited[w] == -1)
dfs(w, sccid);
}