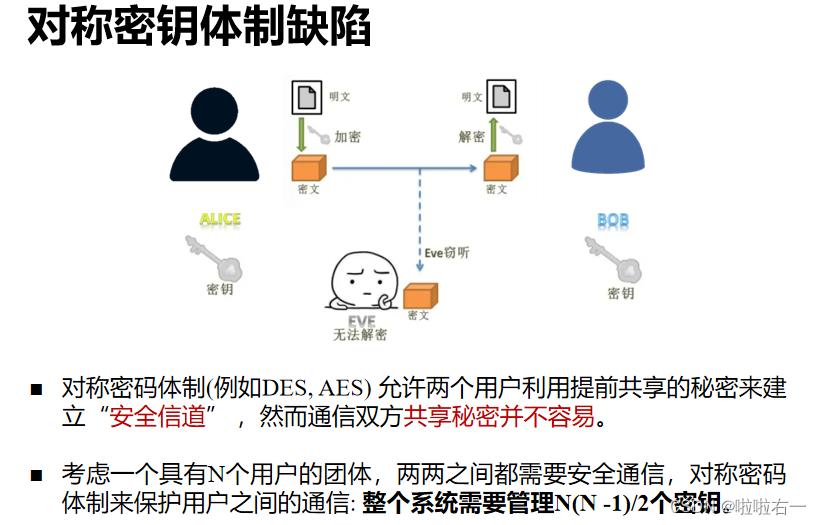
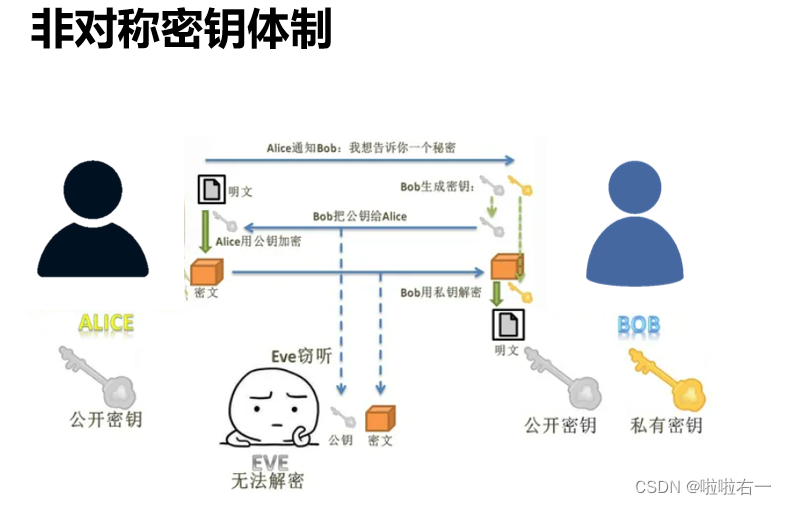
📚关于RSA

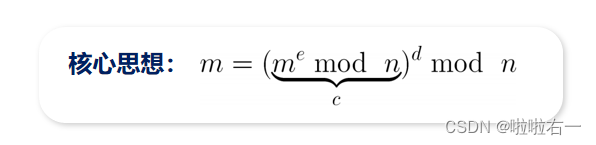
📚实验目的

• 编程实现RSA算法对下列数据实现加密与解密：
  • p=3; q=11, e=7; M=5
  • p=5; q=11, e=3; M=9
  • p=7; q=11, e=17; M=8
  • p=11; q=13, e=11; M=7
  • p=17; q=31; e=7; M=2

📚流程梳理

🐇Step1：求解乘法逆元

• 因为已经给定了p、q、e，所以实际要求的就只剩下乘法逆元d，然后生成密钥函数，再依据算法流程求解即可。

  # 计算a在模m下的乘法逆元
  # 乘法逆元是指对于整数a和模数m，存在一个整数x，使得(a * x) % m = 1
  def modinv(a, m):
     m0, x0, x1 = m, 0, 1
     while a > 1:
        # 计算商q，a%m是余数
        q = a // m
        m, a = a % m, m
        x0, x1 = x1 - q * x0, x0
     return x1 + m0 if x1 < 0 else x1
  

• modinv(a, m) 接收两个参数 a 和 m，分别代表乘法逆元的基数和模数。
• 创建变量：m0, x0, x1 = m, 0, 1。这些变量用于存储中间结果和最终结果。m0 是传入的模数m，x0 和 x1 是扩展欧几里德算法中的辅助变量。
• while 循环：使用除法算法进行迭代，直到 a 变为 1 。在每次循环中进行以下操作：
  • 计算商：q = a // m，将 a 除以 m 的商保存在变量 q 中。
  • 计算余数和更新变量：m, a = a % m, m。m 更新为 a 对 m 取余的结果，a 更新为之前的 m。
  • 更新辅助变量：x0, x1 = x1 - q * x0, x0。根据扩展欧几里德算法的公式更新 x0 和 x1。
• 返回结果：返回计算得到的结果 x1 + m0（如果 x1 小于 0，则加上 m0），这是乘法逆元。

---

1. 背后的理论是扩展的欧几里德算法。欧几里德算法用于计算两个整数的最大公约数，而扩展的欧几里德算法在计算最大公约数的同时，还计算了两个整数的线性组合，也就是计算了乘法逆元。
2. 在每次循环中，通过除法算法计算出 a 对 m 的余数 q 和新的 a。然后根据扩展欧几里德算法的公式，更新辅助变量 x0 和 x1。
3. 当 a 变为 1 或者更小时，循环结束，这时 x1 存储的即为乘法逆元。
4. 最后的返回语句处理了 x1 小于 0 的情况，加上 m0 保证返回的结果是非负的乘法逆元。

🐇Step2：生成密钥

# 生成密钥函数
def generate_key(p, q, e):
    n = p * q
    fyn = (p - 1) * (q - 1)
    d = modinv(e, fyn)
    # print(d)
    return ((n, e), (n, d))

🐇Step3：加密解密

# 加密函数
def encrypt(public_key, plaintext):
    n, e = public_key
    # C = M^e mod n
    ciphertext = pow(plaintext, e, n)
    return ciphertext

# 解密函数
def decrypt(private_key, ciphertext):
    n, d = private_key
    # M = C^d mod n
    plaintext = pow(ciphertext, d, n)
    return plaintext

🐇Step4：最后数据导入

# 测试数据
data = [
    {'p': 3, 'q': 11, 'e': 7, 'M': 5},
    {'p': 5, 'q': 11, 'e': 3, 'M': 9},
    {'p': 7, 'q': 11, 'e': 17, 'M': 8},
    {'p': 11, 'q': 13, 'e': 11, 'M': 7},
    {'p': 17, 'q': 31, 'e': 7, 'M': 2}
]

# 对每组数据进行加密与解密
for d in data:
    p, q, e, M = d['p'], d['q'], d['e'], d['M']
    public_key, private_key = generate_key(p, q, e)
    encrypted_text = encrypt(public_key, M)
    decrypted_text = decrypt(private_key, encrypted_text)
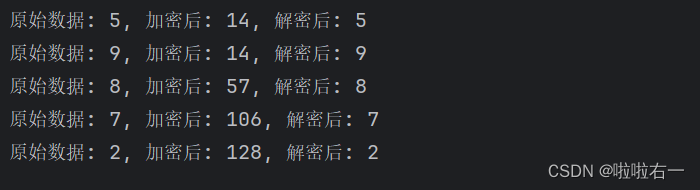
    print(f"原始数据: {M}, 加密后: {encrypted_text}, 解密后: {decrypted_text}")

📚实验结果