在计算机系统中，内存管理是一个至关重要的组成部分，而分页机制和分段机制是两种常见的内存管理方式。一个引人疑惑的问题是：为什么分页机制中逻辑地址空间是一维的，而分段机制中逻辑地址空间是二维的呢？在本文中，我们将深入探讨这个问题，并解释这两种不同的地址空间维度。

1. 分页机制中的一维逻辑地址空间

分页机制采用的是一维逻辑地址空间，即通过一个地址就能唯一确定内存中的位置。在这种机制下，逻辑地址包含一个页号和页内偏移。举例来说，如果页面大小为8位，逻辑地址为1101，我们可以直接通过除法操作得到页号（1101 / 8 = 137），而余数则是页内偏移（1101 % 8 = 5）。通过页号，我们能够迅速找到对应的页表项，从而确定内存中的具体位置。这简化了地址转换过程，使得逻辑地址的表示更为直观和方便。

2. 分段机制中的二维逻辑地址空间

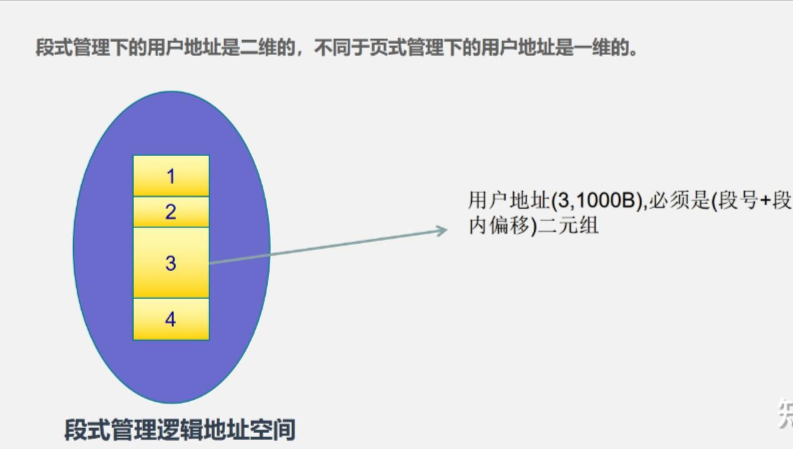
相对于分页机制，分段机制采用的是二维逻辑地址空间，需要两个参数来确定内存中的位置，即段号和段内偏移。在分段机制下，用户程序提供的逻辑地址是一个包含段号和段内偏移的二元组。例如，常见的PC表示为CS::EIP，即代码段::段内偏移。由于段的长度不确定，采用一维地址空间无法准确表示逻辑地址，可能导致歧义。通过使用二维地址，即（段号，段内偏移），可以清晰地描述内存中的位置，解决了地址翻译的歧义问题。

这里更笼统的说一下：

相信大家找寻这个问题就是奔着二维这个来的。本人最开始就陷入了系统角度的思维。

铁子们看见这个图？是不是想着和分页一个道理呢？此时有人心中想着：我可以设置一个最大段长，前n位为偏移量，后m位位段号。——>你这个想法倒是挺好？合适吗？

这里举出分段系统的逻辑地址，记住，这是某个段的逻辑地址，前m位为段号，后n位为段内偏移量，2^n这个段的段长，它针对的是某个段，而不是操作系统为每个段统一定好的，意思就是m和n是不能确定的。

对于段式管理光靠一个逻辑地址，得不到数据的物理地址。因为想要得到物理地址，我们必然要去段表查找，但是去段表查找，又需要段号，我们无法根据这一逻辑地址得到段号，不能像页式管理一样通过除法来得到段号。所以，想要完整描述一个物理地址，必然需要给出(段号，段内偏移)这两个数据，即二维地址。

3. 比较分页与分段的地址管理方式

在分页机制中，通过除法运算直接得到页号，而在分段机制中，用户提供的逻辑地址需要经过段表查找才能获取段号。这一差异导致了地址空间维度的不同，使得分页机制的逻辑地址是一维的，而分段机制的逻辑地址是二维的。