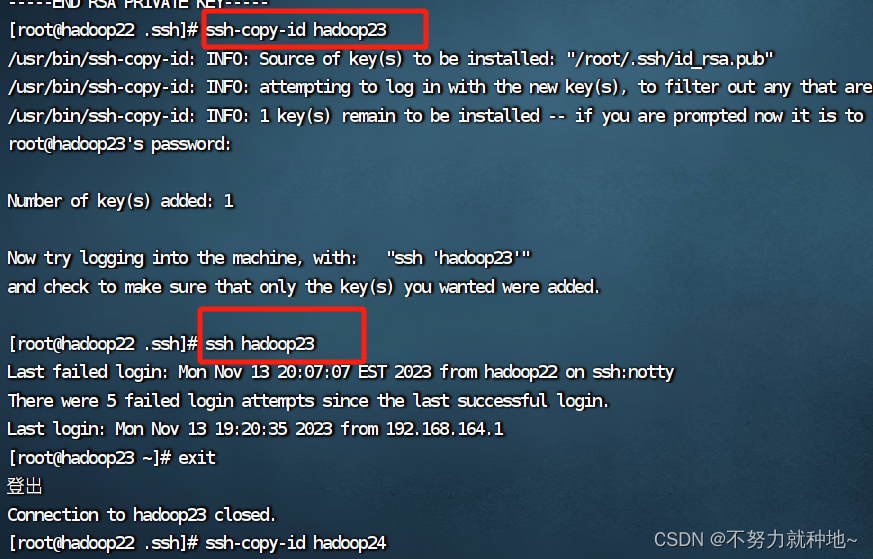
——一元二次函数——【图像→交点】
——【$a{x}^2+bx+c=y$二次函数核心在于“图像”：整体可以由： 图像（形状，上下，交点） $⟹$ $△$ $⟹$ 抛物线与x轴交点 $⟹$ 交点图形】
——【固定做题法：
$⟹$ 一看开口方向：（注意自然语言的表达以决定对二次项系数a是否等于0进行分类讨论）二次函数，二次方程，二次不等式，抛物线（默认a≠0）；函数，方程，不等式（需要对a是否等于0进行分类讨论）
$⟹$ 二看判别式：$△=b^2-4ac$
$⟹$ 三看对称轴：$x=-\frac{b}{2a}$
$⟹$ 四看交点值：顶点坐标：$(-\frac{b}{2a},\frac{4ac-b^2}{4a})$。当$△=b^2-4ac>0$时，函数图象与x轴有两个不同的交点$M_1(x_1,0),M_2(x_2,0)$，则$|M_1{M}_2|=|x_1-x_2|=\frac{\sqrt{△}}{|a|}$。】
1.三种函数形式：
一般式：$y=a{x}^2+bx+c(a\ne 0)$
配方式/顶点式：$y=a(x+\frac{b}{2a}{)}^2+\frac{4ac-b^2}{4a}$，对称轴为$x=-\frac{b}{2a}$，顶点坐标为$(-\frac{b}{2a},\frac{4ac-b^2}{4a})$
两根/零点式：$y=a(x-x_1)(x-x_2)$，$x_1,x_2$是函数的两个根，对称轴为$x=\frac{x_1+x_2}{2}$

2.图像特点：
图像形状：二次函数$y=a{x}^2+bx+c(a\ne 0)$的图像是一条抛物线。——【图像的全身】
开口方向：由a决定，当a＞0时，抛物线开口向上；当a＜0时，抛物线开口向下。——【图像的嘴巴】
对称轴：以$x=-\frac{b}{2a}$为对称轴。——【图像的比例】
顶点坐标：$(-\frac{b}{2a},\frac{4ac-b^2}{4a})$。——【图像的头部】
y轴截距：c，c决定抛物线与y轴交点的位置，影响顶点高度。
定义域：一般隐藏在判别式大于等于零中。
最值：当a＞0（a＜0）时，有最小（大）值$\frac{4ac-b^2}{4a}$，无最大（小）值。——【需验证对称轴是否在定义域内，在则可套用顶点坐标求最值】
单调性：当a>0时，抛物线开口向上，函数在$(-\infty ,-\frac{b}{2a}]$上递减，在$[-\frac{b}{2a},+\infty )$上递增，当$x=-\frac{b}{2a}$时，$f(x{)}_{min}=\frac{4ac-b^2}{4a}$；当$a＜0$时，抛物线开口向下，函数在$(-\infty ,-\frac{b}{2a}]$上递增，在$[-\frac{b}{2a},+\infty )$上递减，当$x=-\frac{b}{2a}$时，$f(x{)}_{max}=\frac{4ac-b^2}{4a}$。——【】
交点图像：当$△=b^2-4ac>0$时，函数图象与x轴有两个不同的交点$M_1(x_1,0),M_2(x_2,0)$，则$|M_1{M}_2|=|x_1-x_2|=\frac{\sqrt{△}}{|a|}$。——【图像的内部】

3.参数含义：二次函数$y=a{x}^2+bx+c(a\ne 0)$
a：当a＞0（a＜0）时，有最小（大）值$\frac{4ac-b^2}{4a}$，无最大（小）值。
b：影响对称轴位置，因以$x=-\frac{b}{2a}$为对称轴。——【a,b决定对称轴的位置】
c：代表图像在y轴上的截距（纵截距），影响顶点高度，因顶点坐标为$(-\frac{b}{2a},\frac{4ac-b^2}{4a})$。

4.图像与x轴的位置：
已知函数$y=a{x}^2+bx+c$与x轴交点的个数，可知
（1）若函数与x轴有2个交点，则$a\ne 0和△=b^2-4ac＞0$；——【【易错点】此类题易忘掉一元二次函数（方程、不等式）的二次项系数不能为0。要使用$△=b^2-4ac$，必先看二次项系数是否为0。】
（2）若函数与x轴有1个交点，即抛物线与x轴相切或图像是一条直线，则$a\ne 0和△=b^2-4ac=0$；或$a=0和b\ne 0$；
（3）若函数与轴没有交点，则$a\ne 0和△=b^2-4ac＜0$或$a=b=0和c\ne 0$。
（4）图像始终位于x轴上方，则$a＞0和△=b^2-4ac＜0$
（5）图像始终位于x轴下方，则$a＜0和△=b^2-4ac＜0$

5.图像与一次函数的交点：
二次函数$y=a{x}^2+bx+c$与一次函数$y=kx＋m$的交点情况有三种，利用数形结合思想，令两函数值相等，得到新的一元二次方程$a{x}^2+bx＋c-(kx+m)=0$。
（1）2个交点：新的一元二次方程$△＞0$。
（2）1个交点：①一次函数与二次函致相切，新的一元二次方程$△=0$。特别地，在顶点处相切时，$k=0$，一次函数为$y=\frac{4ac-b^2}{4a}$。②一次函数垂直于x轴，k不存在。
（3）0个交点：新的一元二次方程$△＜0$。

6.特殊的抛物线$y=a{x}^2+bx+c(a\ne 0)$
（1）若$b=0$，则$y=a{x}^2＋c$，抛物线的对称轴为y轴。
（2）若c = 0，则$y=a{x}^2+bx$，抛物线过原点。
（3）若$b=c=0$，则$y=a{x}^2$，抛物线的对称轴为y轴且过原点。