算法 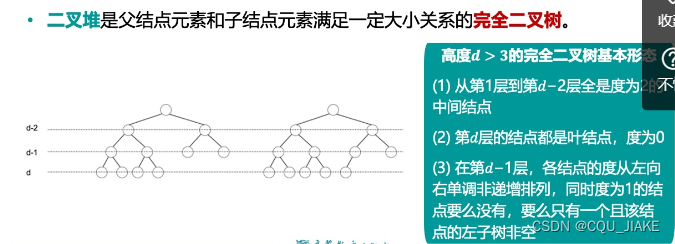
二叉堆的上调
在树上进行的插入排序 。循环次数不会超过树的高度,即插入交换次数不会超过ologn,n是结点个数
![]()
要么到根节点,即i=1结束,要么当前元素还比上面的元素小,直到不比上面的元素小,即h[i/2]<=elem
上调只需要在该分支上不断向上,而下调需要考虑是到左子树还是到右子树,具体就是看那个更小
二叉堆的下调

对于第二点,如果右孩子比根节点小,但是比左兄弟大,那么如果根节点和右孩子交换,右孩子成为根节点后,依然比其左兄弟(此时为左孩子)大,那么依然需要下调。而如果让更小的,即左孩子上来,那么交换完后就不需要调整

二叉堆的插入操作

插入是使堆的大小增加,删除是使堆的大小减少,增加最好不要直接放在顶点上,因为就需要调整两个结点,一个是下调新插入的,一个是放到底下的原顶结点,而如果是上调,就只需要调整新的
二叉堆的删除操作

从堆中取出顶点,然后先记录最后的那个元素,使n-1,之后把最后的结点放在顶点上,开始进行下调调整
二叉堆建堆
两种方式,即不断的上调和下调的区别
朴素建堆是上调操作

一共N个结点,每个结点都要logn的复杂度,所以时间复杂度是nlogn
上调建成的堆和下调建成的堆不一样
一些性质
把一棵树转换为二叉树后,这棵二叉树的形态是( A )。
A. 唯一的
对于完全二叉树,有
顺序存储n个结点的二叉树,完全二叉树需要的空间最小

只有完全二叉树才能顺序存储,或者说顺序存储只适合于完全二叉树
就是说,只有完全二叉树,才能保证数组都是连续的,中间没有空缺的元素,不然数组一定不连续,中间一定有空缺的元素

3个结点可能构造出5种形态的二叉树
设叶子节点个数为n0,度为1的节点个数为n1,度为2的节点个数为n2,必有 n0+n1+n2 = n
(1) 对于二叉树有: n0 = n2+1
这个1是根节点,即n0+n1+n2=2n2+n1+1。
一个节点如果只有一个子节点,那么它的度就是1,除了根节点以外,每个结点都有自己的父节点,所以只需要把所有的度加起来就是除了根节点以外的所有结点的数量和
对于n=2n2+n1+1。如果n为奇数,由于2n2一定是偶数,所以n1一定是偶数
如果N为偶数,那么n1一定是奇数
对于完全二叉树,完全二叉树只可能有一个度为1的结点,即形成满二叉树的过程,满二叉树只有度为0和2的结点
一个满二叉树(完全二叉树)是指一个二叉树,其中每个层次除了最后一层可能不足最大容量外,其它层都是最大容量,而且最后一层从左到右所有节点都是满的
一个节点如果只有一个子节点,那么它的度就是1。因此,如果一个二叉树没有度为1的节点,那么它的所有节点的度都只能是0或2。这意味着每个节点都有两个子节点(除了叶子节点,它们没有子节点)。然而,这并不意味着该树是满二叉树。
一个满二叉树的特征是,除了最后一层可能不足最大容量外,其它层都是最大容量,而且最后一层从左到右所有节点都是满的。对于一个给定的层数,满二叉树的节点数量可以通过公式2^i - 1(i是层数)计算得出。
满二叉树的总结点数一定是奇数,因为每层结点数都是偶数,即2^(k-1),
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结
点总数是(2^k) -1 ,则它就是满二叉树。
一颗树深度为h,最大层数为k,深度与最大层数相同,k=h;
它的叶子数是: 2^h 第k层的结点数是: 2^(k-1) 总结点数是: 2^k-1 (2的k次方减一) 总节点数一定是奇数。满二叉树是完全的完全二叉树
设一棵完全二叉树共有699个节点,则在该二叉树中叶子节点数为?
由于n=2n2+n1+1,总结点数为奇数,所以N1为偶数,由于为完全二叉树,只可能为0,得n2=349,则n0=n-n2=n2+1,即350

向下取整再+1


二叉链表存储树,就是孩子兄弟表示法存储树
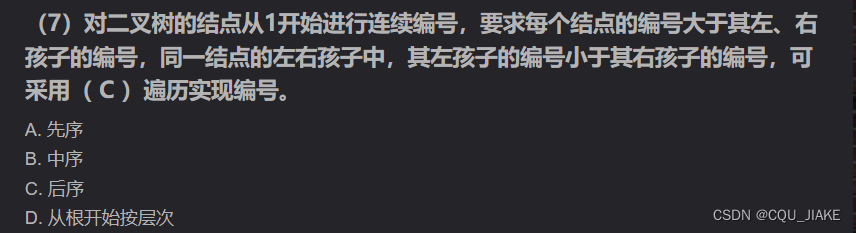
所谓编号,实际上就是每个结点被访问到的序号,也就只需要保证按照一定的顺序去遍历这个树

n=n0+n1+n2+n3+n4=4n4+3n3+2n2+n1+1

顺序存储不适用存储树,最好用来存储完全的树