1.定义

树型结构是一类重要的非线性数据结构，是以分支关系定义的层次结构。是一种一对多的逻辑关系。

树型结构是结点之间有分支，并且具有层次关系的结构，它非常类似于自然界中的树。树结构在客观世界中是大量存在的，例如家谱、行政组织机构都可用树形象地表示。树在计算机领域中也有着广泛的应用，例如在编译程序中，用树来表示源程序的语法结构；在数据库系统中，可用树来组织信息；在分析算法的行为时，可用树来描述其执行过程。等等。

树(Tree)是n (n≥0)个结点的有限集T，T为空时称为空树，否则它满足以下条件：  

 (1) T中有且仅有一个结点K0没有前驱，称K0为树的根结点(Root)。    

(2) 除根结点以外，其余结点有且仅有一个直接前驱。

(3) T中各结点可以有0个或多个后继。  

(4) 当n ≥ 1时，除根结点以外，其余结点可分为m(m≥0)个互不相交的有限集合T1，T2，…，Tm。其中每个集合又构成一棵树，树T1，T2，…，Tm被称为根结点K0的子树(Subtree)。    

树的逻辑结构表示数据之间的关系是一对多，或者多对一的关系。它的结构特点具有明显的层次关系，是一种十分重要的非线性的数据结构。

注：树的定义具有递归性，即树中还有树。

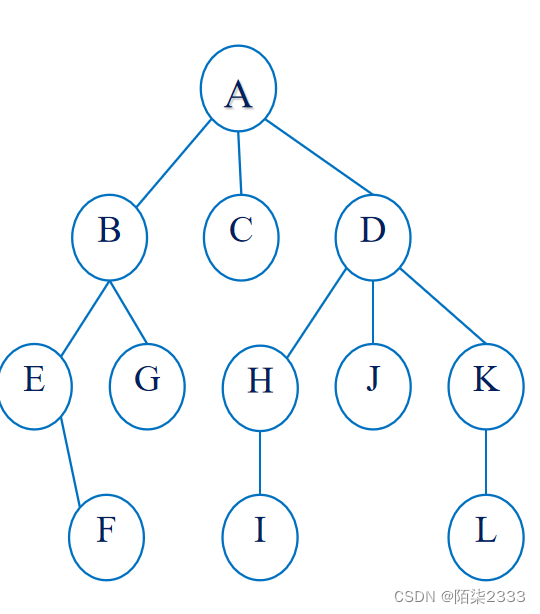
2.树的基本术语

1.父母、孩子与兄弟结点

结点的直接前驱结点称为双亲（parents）结点。

结点的直接后继结点称为孩子（child）结点。

拥有同一个父母结点的多个结点之间称为兄弟（sibling）结点。

结点的祖先（ancestor）是指从根结点到其双亲结点所经过的所有结点。（祖先结点）

结点的后代（descendant）是指该结点的所有孩子结点，以及孩子的孩子等。 （子孙结点）

祖先与后代的关系则是对父子关系的延伸，其定义了树中结点的纵向次序 。

2.度

结点的度（degree）是指结点所拥有子树的棵数。

度为零的结点称为叶子（leaf）或者终端结点

度不为零的结点称为分支结点或者非终端结点、非叶结点。

树的度是指树中各结点度的最大值。

3.结点层次、树的高度

结点的层次（level）属性反映结点处于树中的层次位置。

约定根结点的层次为1，其余结点的层次是其父母结点的层次加1.

树的高度（height）或深度（depth）是树中结点的最大层次数。

4.边、路径

设树中X结点是Y结点的父母结点，有序对（X，Y）称为连接这两个结点的分支，也称为边（edge）。

设（X0，X1，…，Xk-1）是由树中结点组成的一个序列，且（Xi，Xi+1）（0≤i＜k-1）都是树中的边，则该序列称为X0到Xk-1的一条路径（path）。

路径长度（path length）为路径上的边数。

5.无序树、有序树

若把树中每个结点的各子树看成从左到右有次序的（即不能互换），则称该树为有序树（Ordered Tree）；否则称为无序树（Unordered Tree）

如果规定k1和k2是兄弟，且k1在k2的左边，则k1的任一子孙都在k2的任一子孙的左边，则定义了树中结点的横向次序

6.森林

森林（Forest）是m（m≥0）棵互不相交树的集合。

给森林加上一个根结点就变成一棵树。

将树的根结点删除就变成森林。

3.树的表示方法

1.图形表示法

2.嵌套集合表示法

3.广义表表示法

根作为由子树森林组成的表的名字写在表的左边

4.凹入表示法（目录表示法）

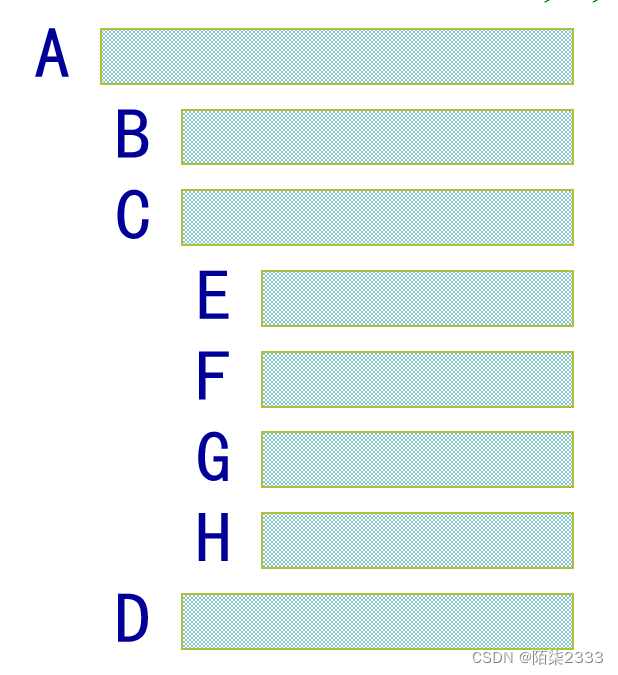
4.抽象数据类型

ADT Tree{
     数据对象：D是具有相同属性的数据元素的集合。
     数据关系：若D为空集，则称为空树；若D仅含一个数据元素，则R为空集，否则R={H}，H是如下二元关系：
　 (1) 在D中存在唯一的称为根的数据元素root， 它在关系H下没有前驱。 
   (2) 除root以外， D中每个结点在关系H下都有且仅有一个前驱。 
 基本操作：
       void CreateTree(Tree *t，definition)：
               初始条件：树t不存在。
               操作结果：按definition构造树t。
        int TreeEmpty（Tree t）：
             初始条件：树t存在 。
            操作结果：若t为空树， 则返回1， 否则返回0。
        int TreeDepth(Tree t)
             初始条件：树t存在。
            操作结果：返回树t的深度。
         ……
}