目录
前言
Topk问题
1.问题描述
2.解决方法
3.代码实现(C/C++)
前言
在人工智能算法岗位的面试中,TopK是问得最多的几个问题之一:
到底有几种方法?
这些方案里蕴含的优化思路究竟是怎么样的?
为啥TopK这么受欢迎呢?究其原因,还是因为它不仅在AI领域广泛应用,比如max pooling,mAP计算等;还涵盖了算法专业的很多必备知识,比如快速排序,二分查找,分治减治,大小顶堆等;一些适当的变换,还可以考察应聘者的思维灵活度。
下面的文章转自架构师之路,是笔者见过此类文章中总结的最透彻的一篇,为了行文流畅,文章有增删。
前段时间我们学习过了数据结构堆以及堆排序算法,堆是一种完全二叉树,那今天我们学习堆的应用,解决topk问题,下面就一起来看看吧。
(相关链接:数据结构-----堆(完全二叉树)-CSDN博客)
Topk问题
1.问题描述
从arr[1, n]这n个数中,找出最大的k个数,这就是经典的TopK问题。
看上去是不是非常直白明了呢?那确实是,但是怎么去解决这个问题?当然我们会想到排序去处理,把这个数组进行排序,然后直接就可以找到了。但是排序的话会把一些不必要的数进行排序处理,也就是说时间复杂度会比较大,但是如果我们单单对前k个大的数字进行单独处理,那效果是不是更好呢?下面我们就看一看堆是怎么实现的。
2.解决方法
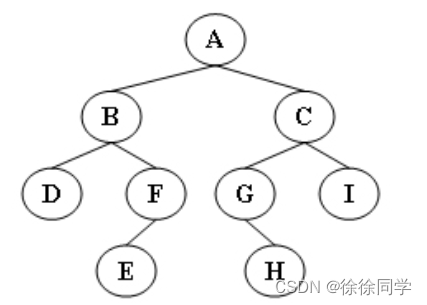
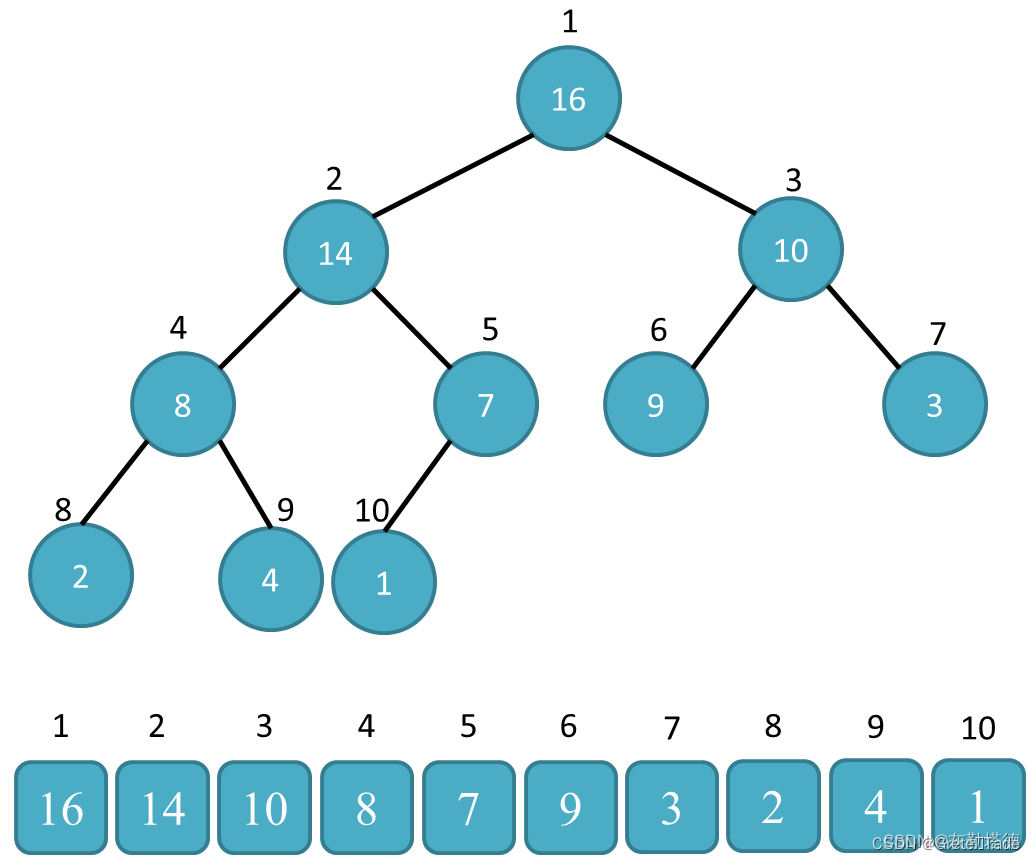
我们获取到当前的数组的时候,然后就创建一个大堆,如图所示,其特点就是上面的元素比下面的元素要大。创建好大堆之后,我们就可以进行后继处理。当前大堆最大的元素就是在第一个位置,我们把第一个位置(最大元素),与最后一个位置的元素进行位置交换,然后把最后一个位置的元素踢出当前的堆,在前面n-1个元素里面再找最大值即可,依次重复以上的操作,执行k次就完成了问题的解决。
3.代码实现(C/C++)
#include<stdio.h>
#include<stdlib.h>
//交换数字
void swap(int* a, int* b) {
int t = *a;
*a = *b;
*b = t;
}
//向下调整
void adjust_down(int* arr, int par, int n) {
int child = par * 2 + 1;
while (child < n) {
if (arr[child] < arr[child + 1] && child + 1 < n)
child++;
if (arr[par] < arr[child]) {
swap(&arr[par], &arr[child]);
par = child;
child = par * 2 + 1;
}
else
break;
}
}
//函数接口
void Top_k(int* arr, int n,int k) {
//先创建这个堆
for (int i = (n - 1) / 2; i >= 0; i--) {
adjust_down(arr, i, n);
}
//然后就是获取当前堆中的最大值
int end = n - 1;
int count = 0;
while (count < k) {
//当前最大值下标为0,把最大值的数与最后一个数进行交换
swap(&arr[end], &arr[0]);
//end--,把最大值踢出当前堆,然后从剩下的n-1个数字的堆继续找最大值
adjust_down(arr, 0, end);
end--;
count++;
}
printf("前%d大的数是:\n", k);
for (int i = n - 1; i > n - 1 - count; i--) {
printf("%d ", arr[i]);
}
}
int main() {
int arr[] = { 5,1,4,7,8,9,3,4,5,6,7,10,55 };
int k = 3;
Top_k(arr, sizeof(arr) / sizeof(int), k);
}以上就是本期的全部内容了,我们下次见!
分享一张壁纸: