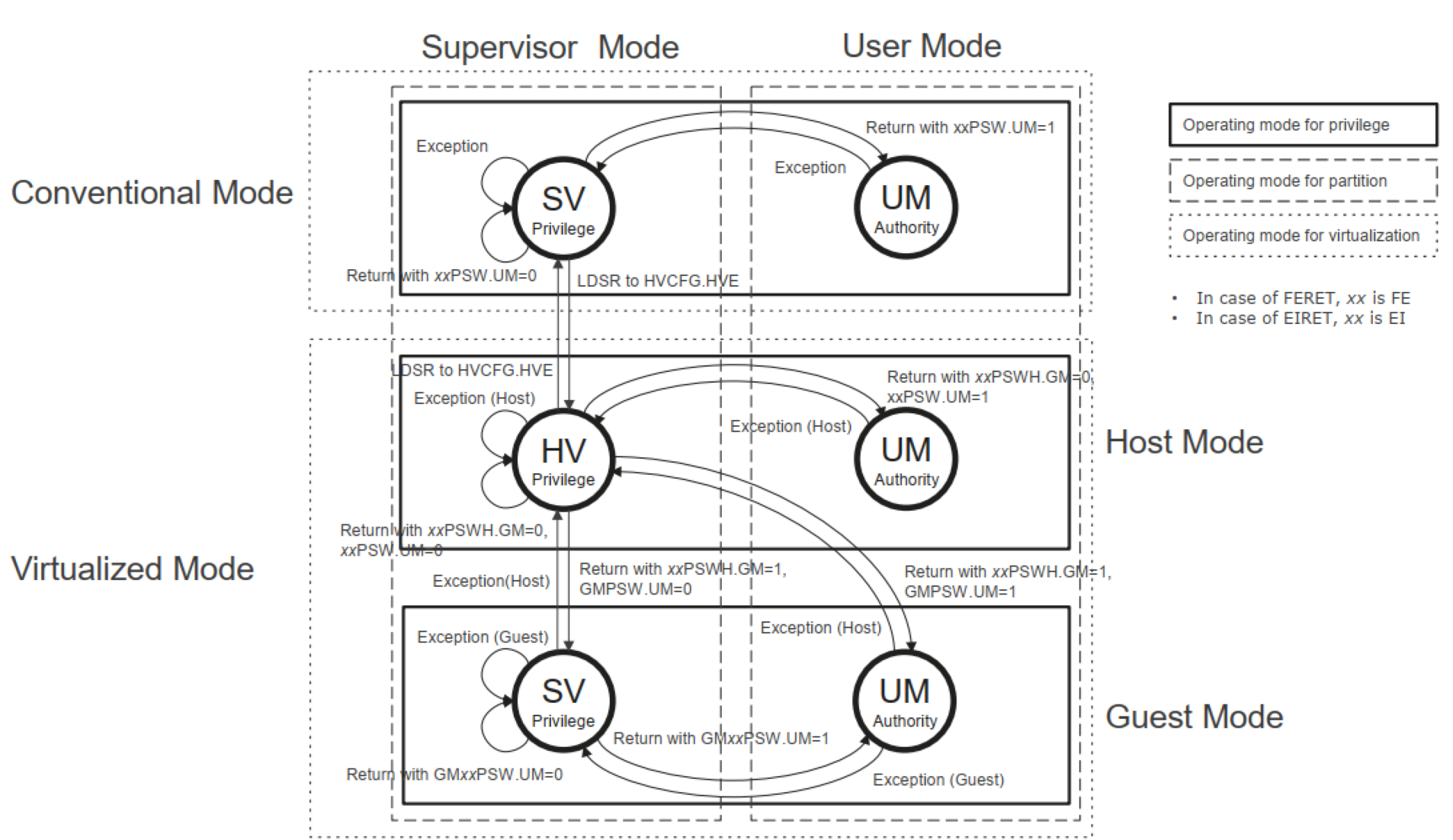
---

题目

LeetCode 189.轮转数组

给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]

解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]

轮转数组是一种将数组中元素向右移动 k 个位置的操作。具体地，我们将数组的最后 k 个元素移动到数组的开头，而数组的前 n-k 个元素向后移动 k 个位置。

说简单点就是把后面的元素，依次转移到前面。

---

暴力求解

算法思路：

1. 定义一个临时变量 tmp，用来存放数组最后的元素7
2. 把数组前 n-1 个值往后挪
3. 把 tmp 的值放入前面空位置中去

这样就完成了 1 次轮转，如果要轮转 k 次，就需要循环 k 次就完成了

第一步：

第二步：

第三步：

代码实现：

void rotate(int* nums, int numsSize, int k)
{
    k %= numsSize;//防止k大于numsSize
    int tmp = 0;
    for (int i = 0; i < k; i++)
    {
        tmp = nums[numsSize - 1];
        for (int j = numsSize - 1; j > 0; j--)
        {
            nums[j] = nums[j - 1];
        }
        nums[0] = tmp;
    }
}

时间复杂度：O(N^2) 最坏情况
空间复杂度：O(1)

---

空间换时间

算法思路：

1. 新开辟一个数组
2. 把后 k 个元素放到新数组的前面
   3 .再把前 n-k 个元素放到新数组的后面（n是数组中元素总个数 也就是题目中的参数 numsSize）

代码实现：

void rotate(int* nums, int numsSize, int k)
{
	if (k > numsSize)
	{
		k %= numsSize;
	}
	int* tmp = (int*)malloc(sizeof(int) * numsSize);

	memcpy(tmp, nums + numsSize - k, sizeof(int) * k);
	memcpy(tmp + k, nums, sizeof(int) * (numsSize - k));
	memcpy(nums, tmp, sizeof(int) * (numsSize));
	free(tmp);
	tmp = NULL;
}

时间复杂度：O(N)
空间复杂度：O(N)

---

三段逆置

算法思路：

1. 对前 n-k 个逆置
2. 对后 k 个逆置
3. 整体逆置

封装一个reverse逆置函数，进行操作。reverse 函数用于反转数组中指定范围的元素，这里使用了双指针来实现。

代码实现：

void reverse(int* arr, int left, int right)
{
	while (left < right)
	{
		int tmp = arr[left];
		arr[left] = arr[right];
		arr[right] = tmp;
		left++;
		right--;
	}
}


void rotate(int* nums, int numsSize, int k) 
{
    if(k>numsSize)
    {
        k%=numsSize;
    }
   reverse(nums, 0, numsSize-k-1);//第一段逆置
   reverse(nums, numsSize-k, numsSize-1);//第二段逆置
   reverse(nums, 0, numsSize-1);//第三段逆置
}

时间复杂度：O(N)
空间复杂度：O(1)

---

总结

最优算法：三段逆置>空间换时间>暴力求解

评判哪个方法为最优解，一般是关注该方法运行时的时间复杂度。时间复杂度低，算法计算时间越快，则为做优算法。
对于空间换时间的方法，虽然运行消耗内存增加，但一般不太会关注消耗内存的多少，现在随着技术发展的越来越快，对于内存的成本控制的也越开越低。所以用空间换时间，还是划算的。