文章目录
- 1、珠宝的最高价值
- 2、下降路径最小和
- 3、最小路径和
- 4、地下城游戏
- 5、按摩师
- 6、打家劫舍||
1、珠宝的最高价值
现有一个记作二维矩阵 frame 的珠宝架,其中 frame[i][j] 为该位置珠宝的价值。拿取珠宝的规则为:
只能从架子的左上角开始拿珠宝
每次可以移动到右侧或下侧的相邻位置
到达珠宝架子的右下角时,停止拿取
注意:珠宝的价值都是大于 0 的。除非这个架子上没有任何珠宝,比如 frame = [[0]]。
class Solution {
public:
int jewelleryValue(vector<vector<int>>& frame) {
//创建dp
int row=frame.size();
int col=frame[0].size();
vector<vector<int>> dp(row+1,vector<int>(col+1));
for(int i=1;i<=row;i++)
{
for(int j=1;j<=col;j++)
{
dp[i][j]=max(dp[i-1][j],dp[i][j-1])+frame[i-1][j-1];
}
}
return dp[row][col];
}
};
2、下降路径最小和
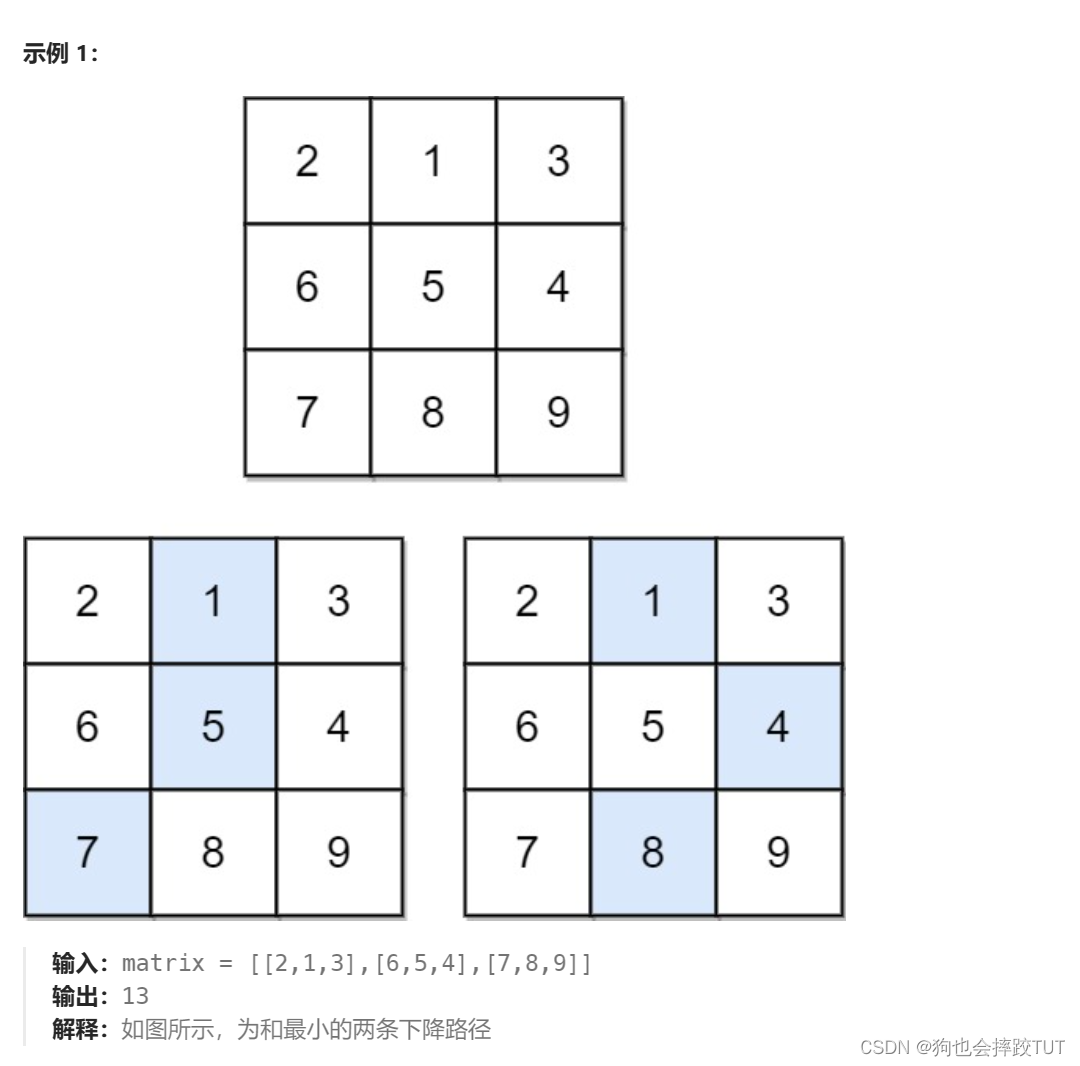
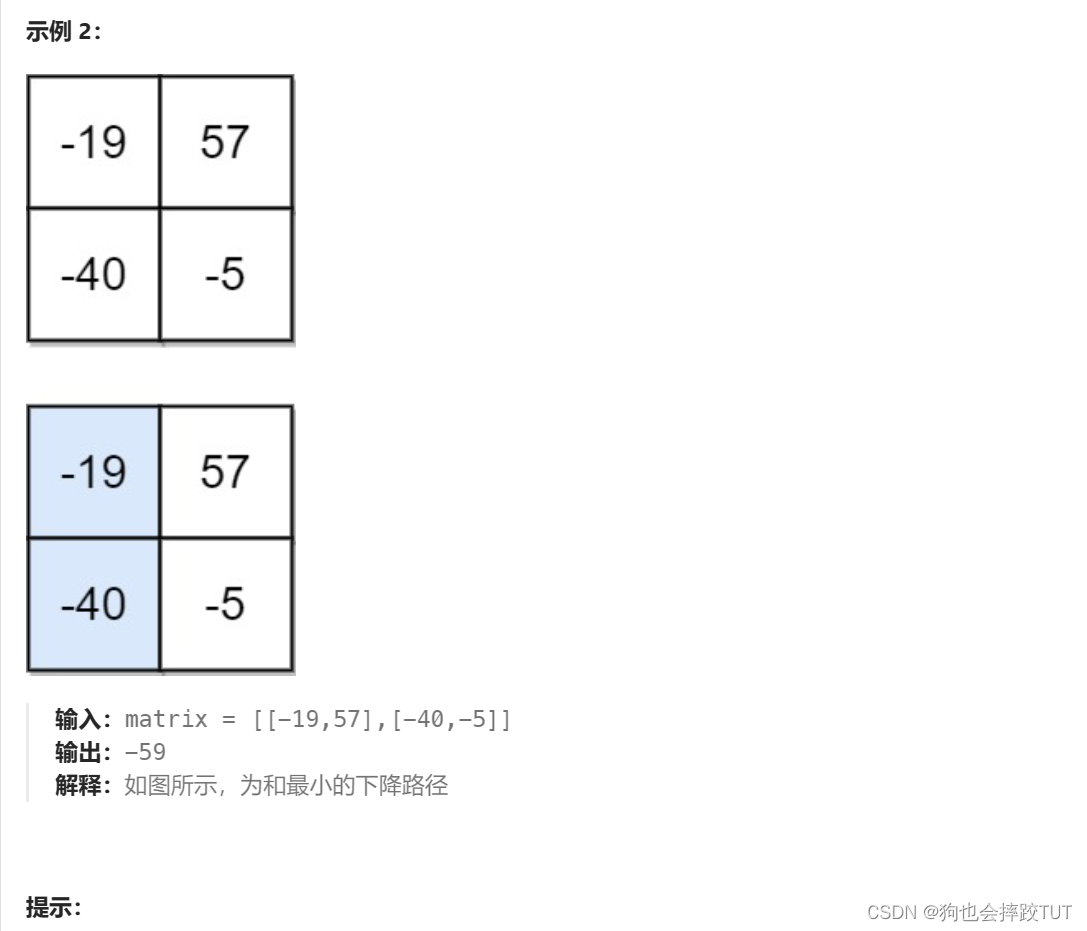
给你一个 n x n 的 方形 整数数组 matrix ,请你找出并返回通过 matrix 的下降路径 的 最小和 。
下降路径 可以从第一行中的任何元素开始,并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列(即位于正下方或者沿对角线向左或者向右的第一个元素)。具体来说,位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。
class Solution {
public:
int minFallingPathSum(vector<vector<int>>& matrix) {
//创建dp
int row=matrix.size();
int col=matrix[0].size();
vector<vector<int>> dp(row+1,vector<int>(col+2,INT_MAX));
//初始化
for(int i=0;i<col+2;i++)
dp[0][i]=0;
for(int i=1;i<=row;i++)
{
for(int j=1;j<=col;j++)
{
dp[i][j]=min(dp[i-1][j-1],min(dp[i-1][j],dp[i-1][j+1]))+matrix[i-1][j-1];
}
}
int dummy=INT_MAX;
for(int i=1;i<=col;i++)
{
dummy=min(dp[row][i],dummy);
}
return dummy;
}
};
3、最小路径和
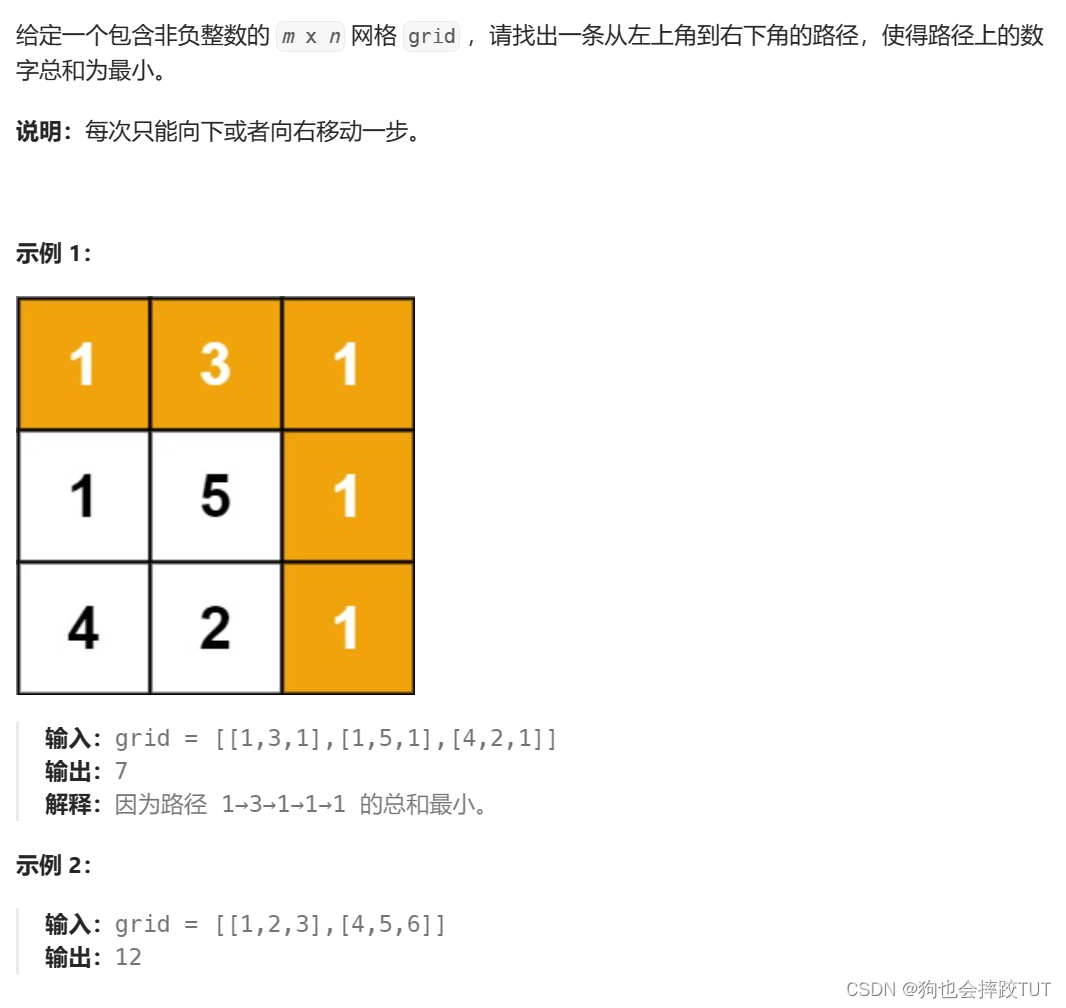
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int row=grid.size();
int col=grid[0].size();
vector<vector<int>> dp(row+1,vector<int>(col+1,INT_MAX));
dp[0][1]=dp[1][0]=0;
for(int i=1;i<=row;i++)
{
for(int j=1;j<=col;j++)
{
dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i-1][j-1];
}
}
return dp[row][col];
}
};
4、地下城游戏
恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快解救公主,骑士决定每次只 向右 或 向下 移动一步。
返回确保骑士能够拯救到公主所需的最低初始健康点数。
注意:任何房间都可能对骑士的健康点数造成威胁,也可能增加骑士的健康点数,包括骑士进入的左上角房间以及公主被监禁的右下角房间。
class Solution {
public:
int calculateMinimumHP(vector<vector<int>>& dungeon) {
//创建dp
int row=dungeon.size();
int col=dungeon[0].size();
vector<vector<int>> dp(row+1,vector<int>(col+1,INT_MAX));
//初始化,以某个位置为起点
dp[row][col-1]=dp[row-1][col]=1;
for(int i=row-1;i>=0;--i)
for(int j=col-1;j>=0;--j)
{
dp[i][j]=min(dp[i+1][j],dp[i][j+1])-dungeon[i][j];
dp[i][j]=max(dp[i][j],1);
}
return dp[0][0];
}
};
5、按摩师
一个有名的按摩师会收到源源不断的预约请求,每个预约都可以选择接或不接。在每次预约服务之间要有休息时间,因此她不能接受相邻的预约。给定一个预约请求序列,替按摩师找到最优的预约集合(总预约时间最长),返回总的分钟数。
class Solution {
public:
int massage(vector<int>& nums) {
//创建dp
int n=nums.size();
if(n==0)
return 0;
vector<int> d(n);//要nums[i]值的数组
auto p=d;//不要nums[i]的数组
//初始化
d[0]=nums[0];
//填表
for(int i=1;i<n;i++)
{
d[i]=p[i-1]+nums[i];
p[i]=max(d[i-1],p[i-1]);
}
return max(d[n-1],p[n-1]);
}
};
6、打家劫舍||
一个专业的小偷,计划偷窃一个环形街道上沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组 nums ,请计算 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。

class Solution {
public:
int ROB(vector<int>& nums,int left,int right)
{
if(right<left) return 0;//注意处理边界问题
int n=nums.size();
vector<int> d(n);//要当前位置的数组
auto p=d;//不要当前位置的数组
//初始化
d[left]=nums[left];
for(int i=left;i<=right;i++)
{
d[i]=p[i-1]+nums[i];
p[i]=max(d[i-1],p[i-1]);
}
return max(d[right],p[right]);
}
int rob(vector<int>& nums) {
int n=nums.size();
return max((nums[0]+ROB(nums,2,n-2)),ROB(nums,1,n-1));
}
};