二分图判定和二分图最大匹配

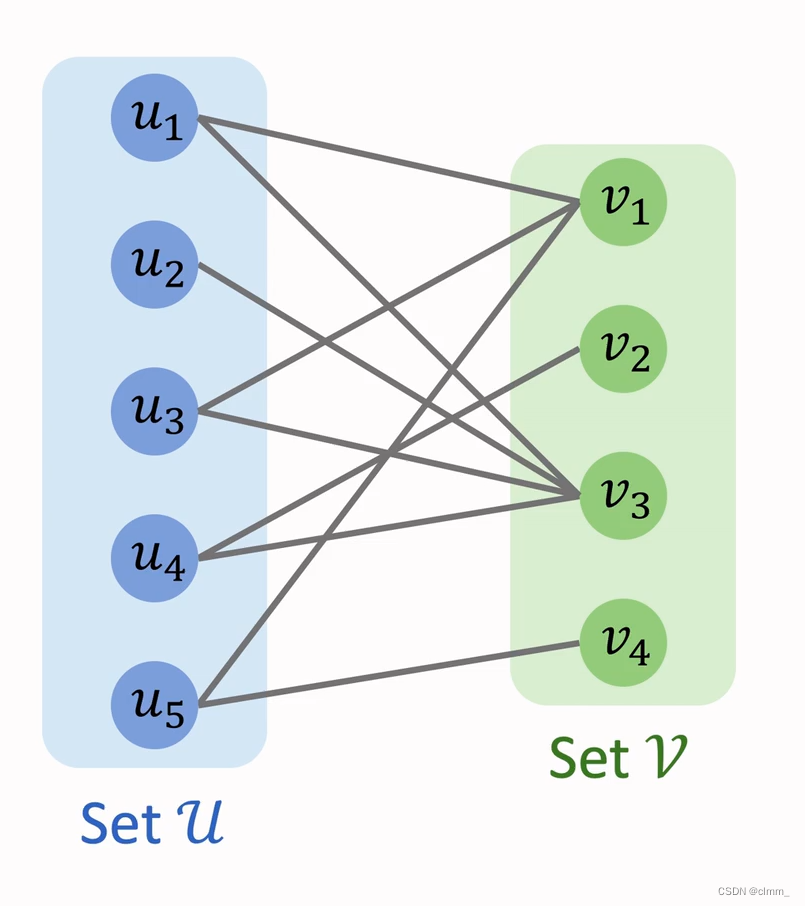
1.二分图的定义

二分图是一种特殊的无向图，它的节点可以被划分为两个互不相交的集合，使得同一集合中的任意两个节点之间没有边相连，而不同集合中的节点之间都有边相连。

换句话说，如果一个无向图可以被划分为两个集合，并且所有边的两个端点都分别属于不同的集合，那么这个无向图就是一个二分图。

如图，有蓝色，绿色两个集合，集合内的点可以跟另一个集合内的点相互连接，但集合内部不能连接，这就叫二分图。

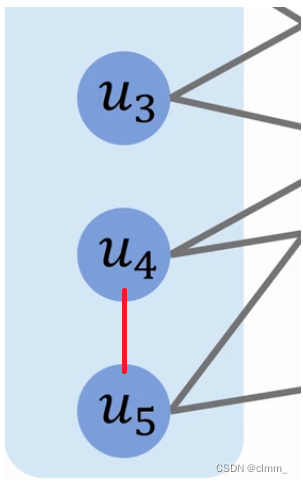
那么如何判定是否为二分图呢？这就要用到二分图的染色

2.二分图的染色

假设图中的颜色都还没标上，只有点和边，那么我们需要对各个点能直达的点染色（也就是不同集合的点的染不同颜色），如果能符合“相邻点的颜色不同”这个条件，就是一个二分图。

反之如下，两个蓝色的点之间有连线，可是他们颜色相同，就不能满足条件了

例题1

1.用vector建图，此时我们已经知道了各个点（记作点i）的所有邻接点（也就是只用走一条边就能到达的点），那么点i的邻接点j的颜色不能跟点i一样

2.如果点i是蓝色，点j就应该被染成绿色

3.我们要将以点i为起点，所有能到达的点都遍历，可以用dfs或者bfs

4.如果染的过程中，某点还没有染色，就将其染成相反色；

如果已经染了色，且颜色为相反色，则不用管；

如果已经染了色，且颜色相同，说明不满足条件，这不是一个二分图。

dfs写法

#include<cstdio>
#include<set>
#include<list>
#include<queue>
#include<math.h>
#include<stdlib.h>
#include<string>
#include<string.h>
#include <stdio.h>
#include<algorithm>
#include<iomanip>
#include<cmath>
#include<sstream>
#include<stack>
#include <utility>
#include<map>
#include <vector>

#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
#define inf 0x3f3f3f3f
//2147483647

#define int long long
//#include <bits/stdc++.h>
typedef long long ll;
#include<iostream>
using namespace std;

const int N = 1e6 + 10;
//long long MAX(long long a, long long b) { return a < b ? b : a; }



vector<int> edge[N];
int vis[N];//0为蓝色，1为绿色
bool ans = true;

void dfs(int cur, int c) {
	//作用：遍历cur能到达的点，并且将这些点染色
	vis[cur] = c;

	for (auto x : edge[cur]) {
		//遍历cur的邻接点
		if (vis[x] == -1) {
			//还未被染色
			dfs(x, 1 - c);
			//将x点染成跟cur不一样的颜色
			//并且开始深搜
		}
		else if (vis[x] == vis[cur]) {
			ans = false;
		}
	}

}
signed main() {
	memset(vis, -1, sizeof vis);
	int n, m; cin >> n >> m;
	while (m--) {
		int a, b; cin >> a >> b;
		edge[a].push_back(b);
		edge[b].push_back(a);

	}
	for (int i = 1; i <= n; i++) {
		if (vis[i] == -1) dfs(i, 1);
	}

	if (ans) cout << "Yes";
	else cout << "No";
	return 0;
}

bfs写法

#include<assert.h>
#include<cstdio>
#include<set>
#include<list>
#include<queue>
#include<math.h>
#include<stdlib.h>
#include<string>
#include<string.h>
#include <stdio.h>
#include<algorithm>
#include<iomanip>
#include<cmath>
#include<sstream>
#include<stack>
#include <utility>
#include<map>
#include <vector>

#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
#define inf 0x3f3f3f3f
//2147483647

#define int long long
//#include <bits/stdc++.h>
typedef long long ll;
#include<iostream>
using namespace std;

const int N = 1e6 + 10;
//long long MAX(long long a, long long b) { return a < b ? b : a; }



vector<int> edge[N];
int vis[N];//0为蓝色，1为绿色
bool ans = true;

void bfs(int cur) {
	//作用：遍历cur能到达的点，并且将这些点染色
	

	queue<int> q;
	q.push(cur);
	vis[cur] = 0;
	while (!q.empty()) {
		int t = q.front();
		
		q.pop();
		for (auto x : edge[t]) {
			if (vis[x] == -1) {
				q.push(x);
				vis[x] = 1 - vis[t];
			}
			else if (vis[x] == vis[t]) {
				ans = false;
				return;
			}
		}

	}

}
signed main() {
	memset(vis, -1, sizeof vis);
	int n, m; cin >> n >> m;
	while (m--) {
		int a, b; cin >> a >> b;
		edge[a].push_back(b);
		edge[b].push_back(a);

	}
	for (int i = 1; i <= n; i++) {
		if (vis[i] == -1) bfs(i);
	}

	if (ans) cout << "Yes";
	else cout << "No";
	return 0;
}

例题2

D - Good Tuple Problem

分析：atcoder周赛，基本就是模板题了

#include<cstdio>
#include<set>
#include<list>
#include<queue>
#include<math.h>
#include<stdlib.h>
#include<string>
#include<string.h>
#include <stdio.h>
#include<algorithm>
#include<iomanip>
#include<cmath>
#include<sstream>
#include<stack>
#include <utility>
#include<map>
#include <vector>

#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
#define inf 0x3f3f3f3f
//2147483647

#define int long long
//#include <bits/stdc++.h>
typedef long long ll;
#include<iostream>
using namespace std;

const int N = 1e6 + 10;
//long long MAX(long long a, long long b) { return a < b ? b : a; }



vector<int> dif[N];//dif[i]存的是，需要跟i结点不同的结点
int a[N], b[N], x[N];
bool ans = true;

void dfs(int i, int s) {
	x[i] = s;
	for (int j = 0; j < dif[i].size(); j++) {
		if (x[dif[i][j]] == -1) {
			dfs(dif[i][j], 1 - s);
		}
		else if (x[dif[i][j]] == x[i]) ans = false;
	}

}
signed main() {
	int n, m; cin >> n >> m;

	for (int i = 0; i < m; i++) {
		cin >> a[i];
	}
	for (int i = 0; i < m; i++) {
		cin >> b[i];
	}
	for (int i = 0; i < m; i++) {
		dif[a[i]].push_back(b[i]);
		dif[b[i]].push_back(a[i]);
	}

	memset(x, -1, sizeof x);
	for (int i = 1; i <= n; i++) {
		if(x[i]==-1) dfs(i, 0);
	}

	if (ans) cout << "Yes";
	else cout << "No";

	return 0;
}

3.匈牙利算法

匈牙利算法是用来求二分图的最大匹配数，注意！是最大匹配数，是无权的

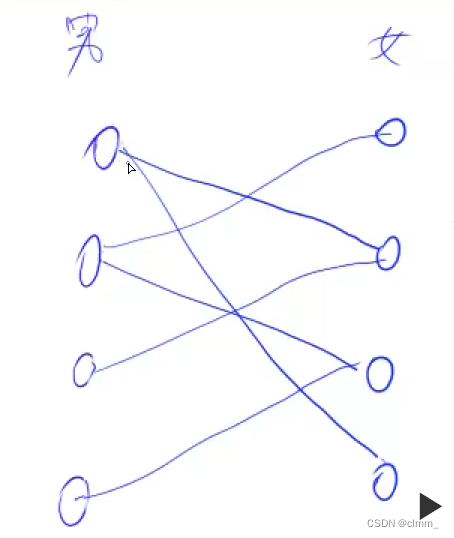
假设有这些男生和女生，男生对一些女生中意，问怎么匹配才能让匹配出来的情侣数量最多

答：我们把下面的行为看成一个“追”的动作

男生i一个个访问自己中意的女生，如果该女生j还没有对象，则直接匹配成功。

如果女生j有对象，即match[j]这个男生，那么去找找看match[j]这个男生能不能换一个女朋友（即女生j有调整空间），然后把女生j让给男生i。如果可以，则男生i也匹配成功。

如果男生i遍历完所有中意的女生还是找不到，就匹配失败。

着重解释一下st[]。作用是不重复访问同一个女生，导致递归陷入死循环。

我们可以把st[]的作用看成一个“预定”的行为，当女生j还没被预定，则使其被预定，即st[j] = true，看看这个女朋友能不能追到手（也就是我上面“答”的部分）。不行的话去看看其他中意的女生。

注意！不论女生j追没追到手，她都已经是被”预定“过了，后续不能再访问。

那到底是怎么陷入死循环的呢？

如果没有st数组的情况如下。

当男生i访问到了女生j，女生j已经有男生k当男朋友了，那么此时就要看看男生k能不能换别的女朋友。所以男生k就会遍历所有自己中意的女生，看看有没有未被选的女生，或者有调整空间的女生。

问题就出在这里！这样的话男生k可能又会访问到女生j，然后看女生j有没有调整空间，也就是自己有没有调整空间，陷入递归死循环！

因此，st[]的存在是必要的。

#include<cstdio>
#include<set>
#include<list>
#include<queue>
#include<math.h>
#include<stdlib.h>
#include<string>
#include<string.h>
#include <stdio.h>
#include<algorithm>
#include<iomanip>
#include<cmath>
#include<sstream>
#include<stack>
#include <utility>
#include<map>
#include <vector>

#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
#define inf 0x3f3f3f3f
//2147483647

#define int long long
//#include <bits/stdc++.h>
typedef long long ll;
#include<iostream>
using namespace std;

const int N = 1e6 + 10;
//long long MAX(long long a, long long b) { return a < b ? b : a; }

int cnt = 0;
int head[N], e[N], ne[N];
int match[N];
bool st[N];

void add(int u, int v) {
	e[cnt] = v, ne[cnt] = head[u], head[u] = cnt++;
}

bool find(int x) {
	//找x能不能配对到女朋友
	
	//遍历x所中意的女生
	for (int i = head[x]; i != -1; i = ne[i]) {
		int j = e[i];
		if (!st[j]) {
			st[j] = true;
			if (match[j]==0 || find(match[j])) {
				//如果女生j没有男朋友，或者女生当前的男朋友可以选择其他女生
				//那么就让那个男生去找别的女生，男生x跟女生j匹配
				match[j] = x;
				return true;
			}

		}

	}
	return false;
}

int a, b, n;
signed main() {
	memset(head, -1, sizeof head);
	cin >> a >> b >> n;
	for (int i = 0; i < n; i++) {
		int u, v, w; cin >> u >> v;
		add(u, v);
	}

	int ans = 0;
	for (int i = 1; i <= a; i++) {
		memset(st, false, sizeof st);
		if (find(i)) ans++;

	}
	cout << ans;

	return 0;
}