软件过程模型:
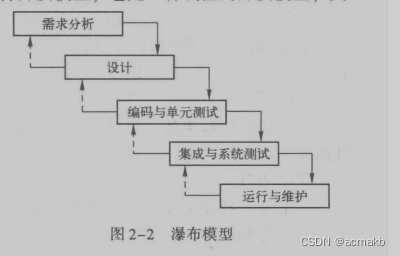
瀑布模型
有很强的前后关联性,前一阶段的输出是后一阶段的输入,而且不可回溯性。
适应场景:
- 软件开发人员经验丰富
- 需求变化少,变更少,可以一次性获取全部需求
- 项目风险低,无法进行风险把控
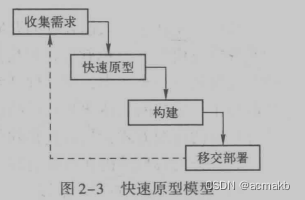
快速原型模型
强调 快速 , 就是快速建立其一个demo,根据用户意见不断进行修改和完善
适应场景:
- 已经有产品demo
- 有快速原型开发工具
- 简单而熟悉的领域
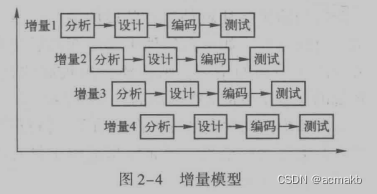
增量模型
项目模块化,组件化,对每一个模块分别进行分析,设计,编码和测试。先将主要功能设计实现,后不断完善模块,可以分批次提交产品
适应场景:
- 软件产品分批次提交
- 软件可以被模块化
- 不用一次性进行系统开发
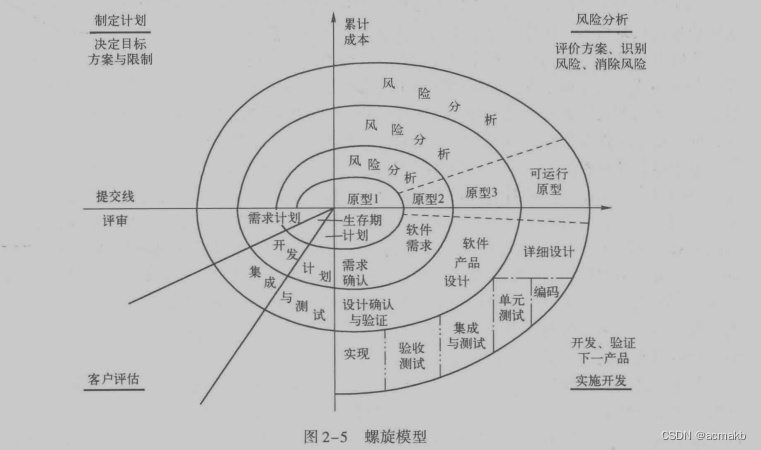
螺旋模型
强调 风险较大 的项目开发,是瀑布模型和快速原型模型的结合版本。包括制订计划、风险分析、实施工程和客户评估4种活动。
适应场景:
- 适合风险较大的项目开发
- 强调对风险的把控
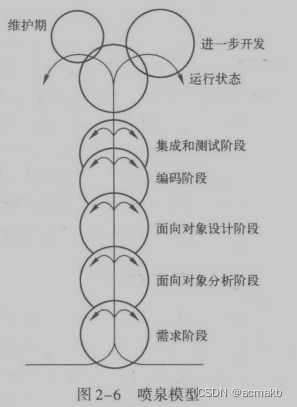
喷泉模型
过程模型,面向对象开发,多次迭代和开发。过程:分析、设计、编码、测试、进一步开发和维护。
- 面向对象的项目
- 可以多次迭代
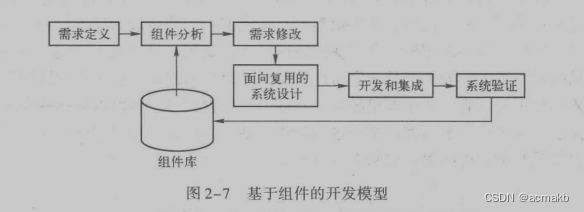
基于组件的开发模型
不是从0-1进行开发,使用现有的组件和框架进行产品开发。比如前端框架Vue,React,后端框架 Spring全家桶,python的Django和Flask框架,这些组件和框架功能完善,开发效率高。
产品基于组件的开发模型充分体现了软件复用的思想,目前绝大多数的软件都是这样开发出来的。
使用场景
- 软件系统庞大
- 高产品质量 低开发成本和风险
统一软件开发过程模型:
基于 UML 的面向对象软件开发模型,的一种面向对象软件开发模型。它解决了螺旋模型的可操作性问题,采用选代和增量递进的开发策略,并以用例驱动为特点,集中了多个软件开发模型的优点。
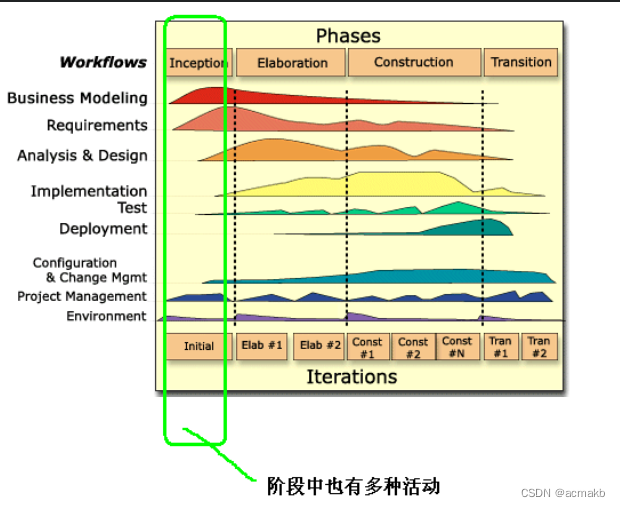
适应场景:
- 适应范围广泛,但是对开发人员素质要求较高