题目给了我们一个二叉树要让我们来判断这一个二叉树是不是平衡二叉树。
要想判断一棵树是不是平衡二叉树，我们得首先知道平衡二叉树的定义是什么，平衡二叉树指的是这样的树它的左子树的高度与右子树高度的差的绝对值不能超过1，而且它的左子树是一颗平衡二叉树，它的右子树也是一颗平衡二叉树。画出图示如下：

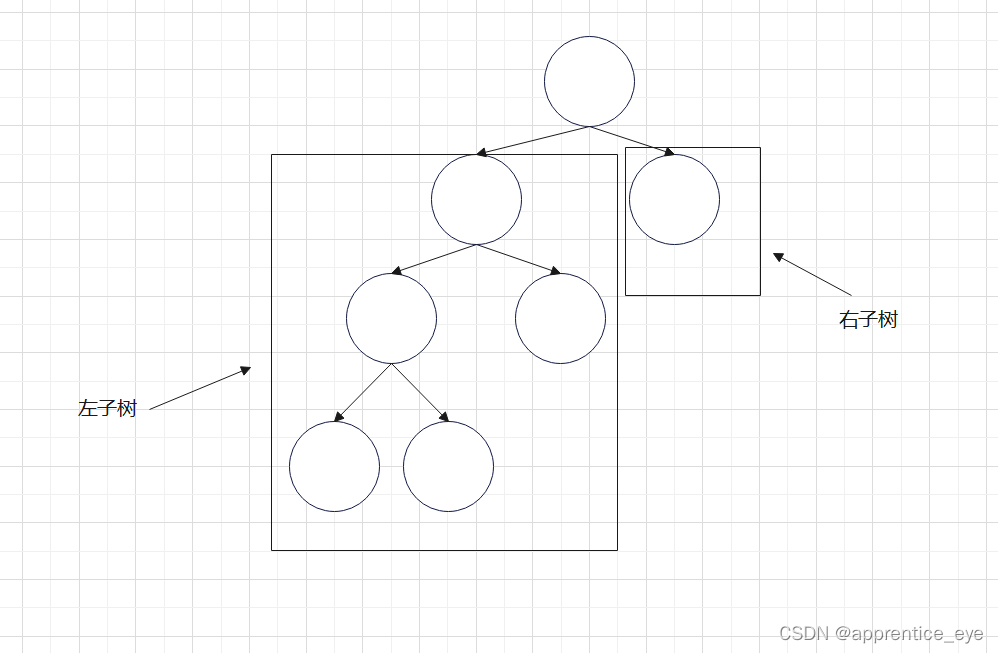
我们可以看出这一个二叉树的左子树是高度为3的一棵树，右子树为高度为1的一颗子树，所以这不是一颗平衡二叉树。

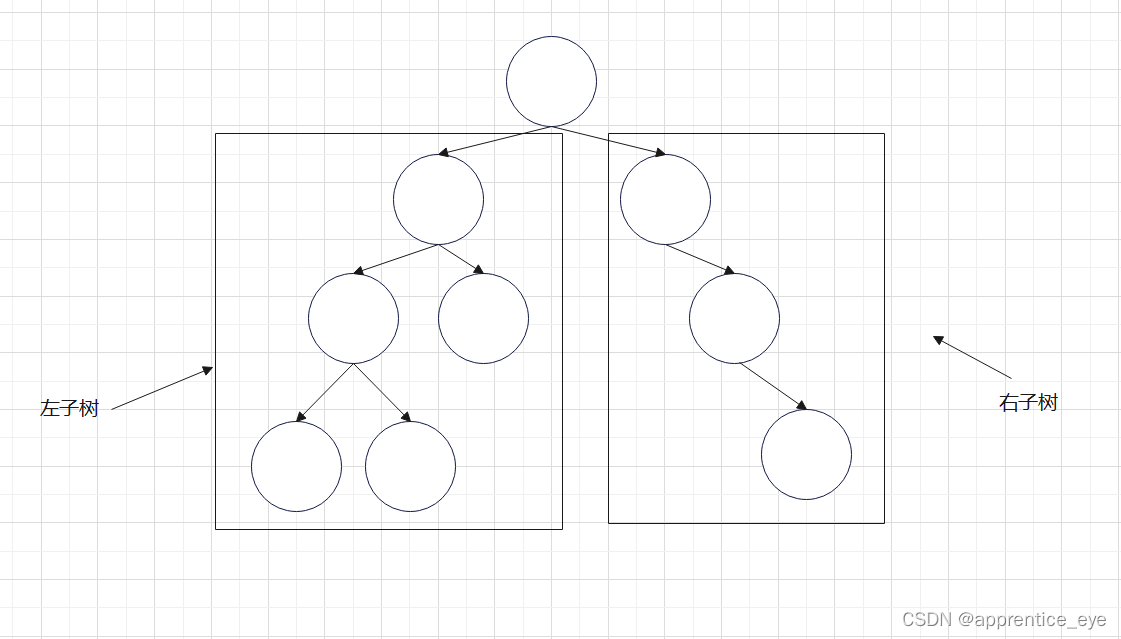
上面这一颗树虽然根结点的左右子树的高度相差0，但是其右子树不是平衡二叉树，所以这一颗树仍然不是平衡二叉树。
相信看到这了，你一定有所感觉，也就是说我们判断一颗二叉树不仅要知道该二叉树的左子树与右子树的高度差，还要求出左子树是否为二叉树右子树是否为平衡二叉树。我们要先知道左子树与右子树是否为平衡二叉树才能知道整棵树是否为平衡二叉树。而子树仍然是一颗二叉树，所以判断二叉树是否为平衡二叉树的方法仍然可以使用，这就涉及到了递归的问题。
那么递归的终止条件是什么？因为叶子结点的指针域为空，没有孩子了，当访问到为空的指针域时就该终止递归了，此时访问到的空指针域可以看作根结点为空的二叉树，该二叉树的高度为0，显然空二叉树是平衡二叉树。这样我们就知道了当访问到$root==NULL$时应该返回该子树高度为0，是平衡二叉树。
那么非终止条件下则应该返回什么呢？非终止条件下，该结点的高度应为两颗子树中高度较大的加1，这就是该子树的高度，知道子树的高度之后，我们还需要根据其左右子树的高度差判断这一项是否符合平衡二叉树的条件，所以我们要求出$-1\le 左子树高度-右子树高度\le 1$同时还要知道其左子树是否为平衡二叉树，右子树是否为平衡二叉树，
将上述命题符号化：
$$\begin{gathered} q:-1\le 左子树高度-右子树高度\le 1 \\ p:左子树为平衡二叉树 \\ s:右子树为平衡二叉树 \end{gathered}$$
当这三项都满足时此树才为平衡二叉树，所以返回的应该是$p\wedge q\wedge s$
有了上面的思路我们可以写出下面的代码：

bool isBalance(struct TreeNode * root, int *depth){
    int *left = (int *)malloc(sizeof(int));
    int *right = (int *)malloc(sizeof(int));
    bool l, r;
    if(root==NULL){
        (*depth) = 0;
        return true;
    }
    l = isBalance(root->left, left);
    r = isBalance(root->right, right);
    *depth = (*left)>(*right)?(*left):(*right);
    *depth = (*depth) + 1;
    int x = (*left)-*right;
    if(x>=-1&&x<=1){
        return true && l && r;
    }
    return false && l && r;
}
bool isBalanced(struct TreeNode* root) {
    int depth = 0;
    return isBalance(root, &depth);
}

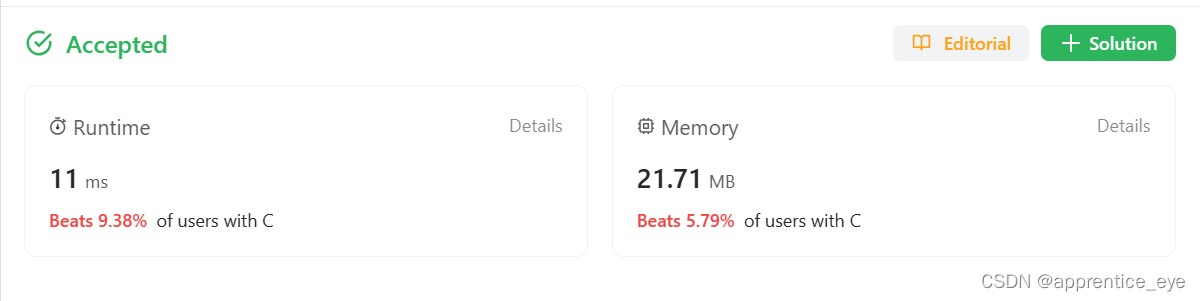
运行结果如下：