目录

题目：

示例：

解题思路：

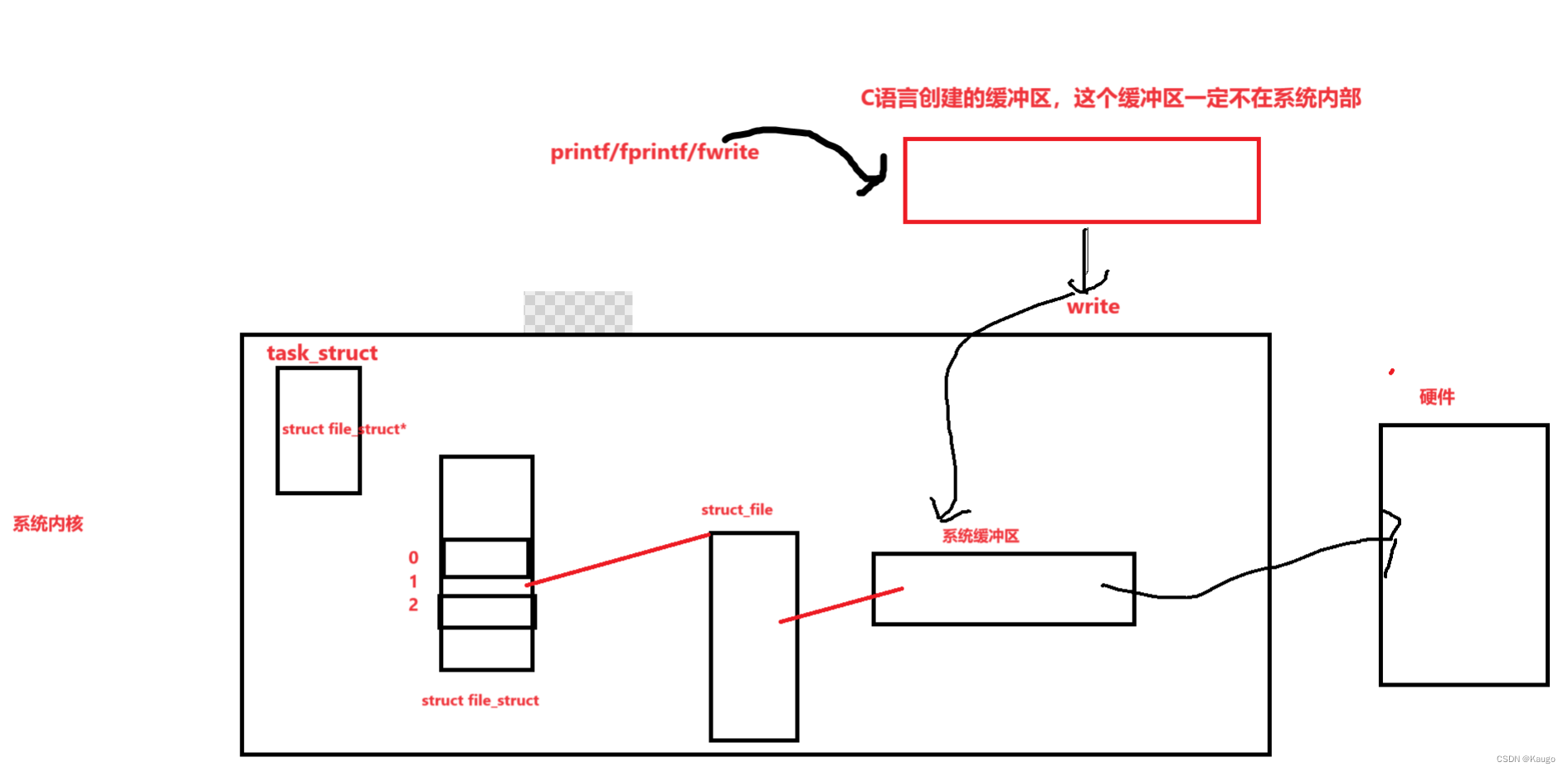
方法一：双链表链接法

图例：

代码演示： 

解题效果： 

方法二：奇偶指针

图例：

代码演示： 

 

题目：

给定单链表的头节点 head ，将所有索引为奇数的节点和索引为偶数的节点分别组合在一起，然后返回重新排序的列表。

第一个节点的索引被认为是 奇数 ， 第二个节点的索引为 偶数 ，以此类推。

请注意，偶数组和奇数组内部的相对顺序应该与输入时保持一致。

你必须在 O(1) 的额外空间复杂度和 O(n) 的时间复杂度下解决这个问题。

题源：328. 奇偶链表 - 力扣（LeetCode）

题目大意：将链表中的索引位是奇数的节点放前面，索引位是偶数的节点放后面。 

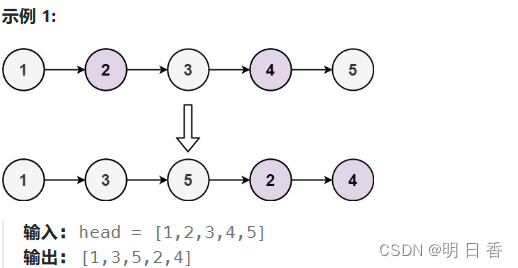
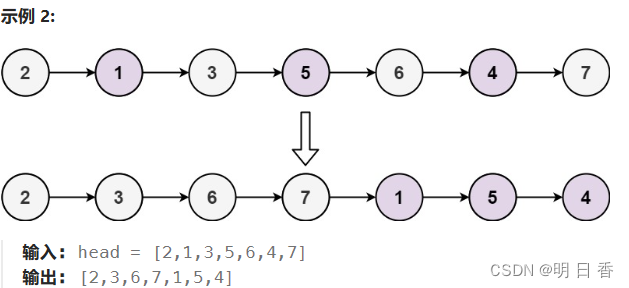
示例：

 

 

解题思路：

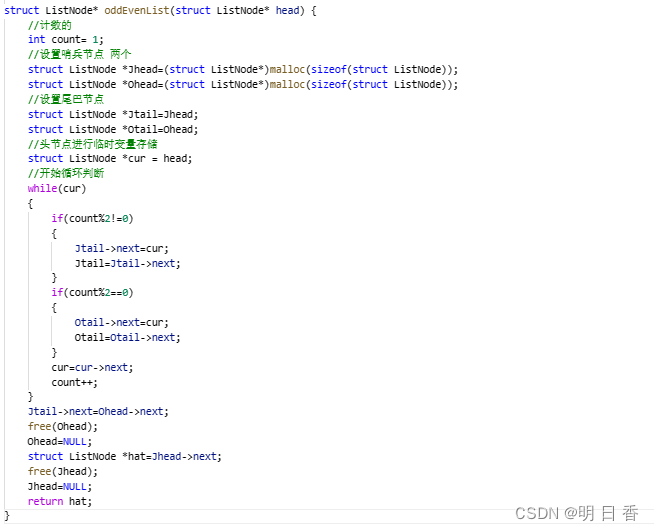
方法一：双链表链接法

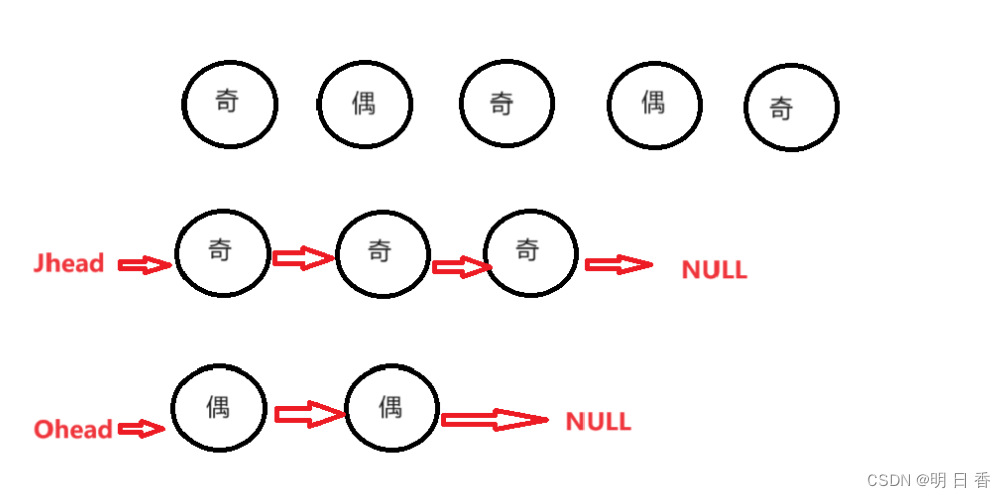
设置两个带有哨兵位的带头节点，分别记住两个哨兵位节点的地址。

在设置一个计数变量，负责计数该节点的索引位，负责之后的判断。

然后，使用尾插的方式，在判断某一节点的索引位的奇偶后，进行插入到两个带头的哨兵链表中。

 最后，奇数链表连接偶数链表，释放哨兵位节点，得出答案。

图例：

 

代码演示： 

 

解题效果： 

 

如上图所示，方法一写完之后会超出题目要求的时间复杂度。

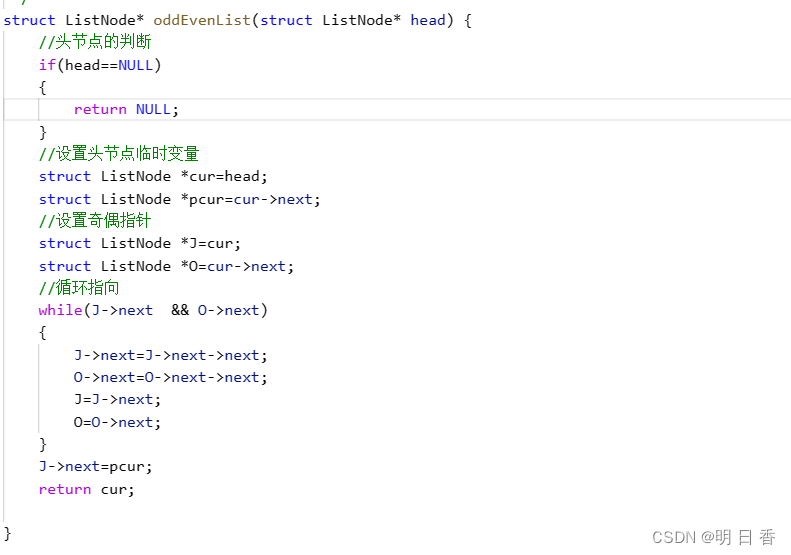
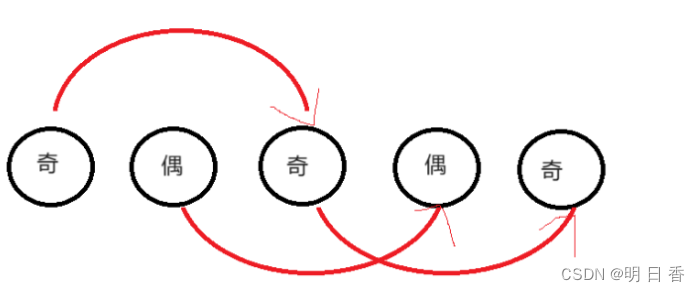
方法二：奇偶指针

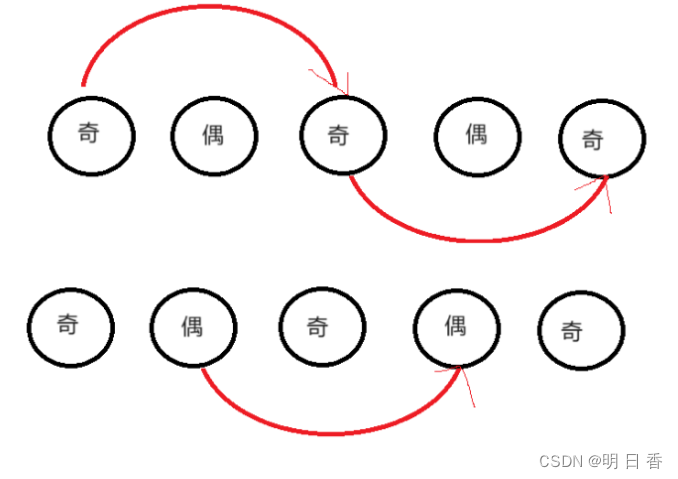
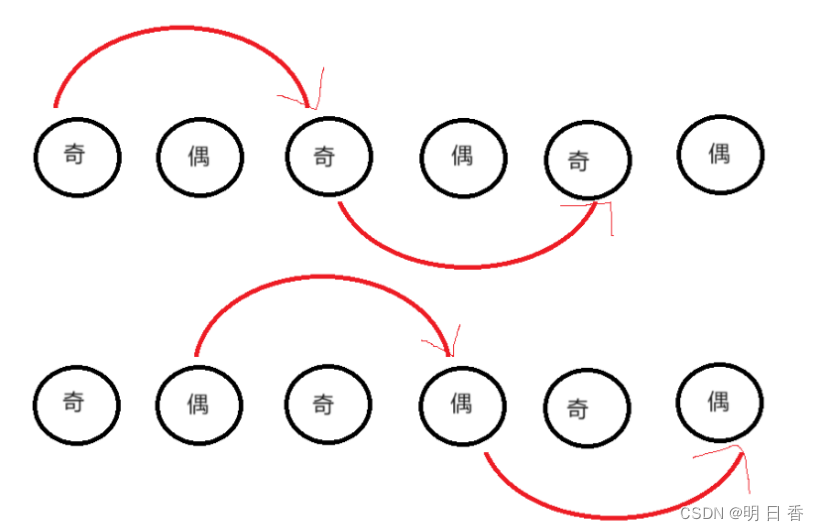
用临时变量指针分别记下原链表的头节点和第二个节点的 地址。

设置两个指针J、O分别指向第一个节点和第二个节点。

而后J指针指向奇数索引位的节点，O指针指向偶数索引位的节点，同时改变指针的指向，最后利用之前设置的临时变量进行返回最后的链表和进行拼接操作。

图例：

 

 

 

代码演示： 

---