通过上期学习,大家已经了解了非线性规划中约束极值问题的最优性条件。本期小编将为大家介绍约束极值问题的求解方法:制约函数法,包括概念以及最基本的两种制约函数法:罚函数法、障碍函数法等内容。
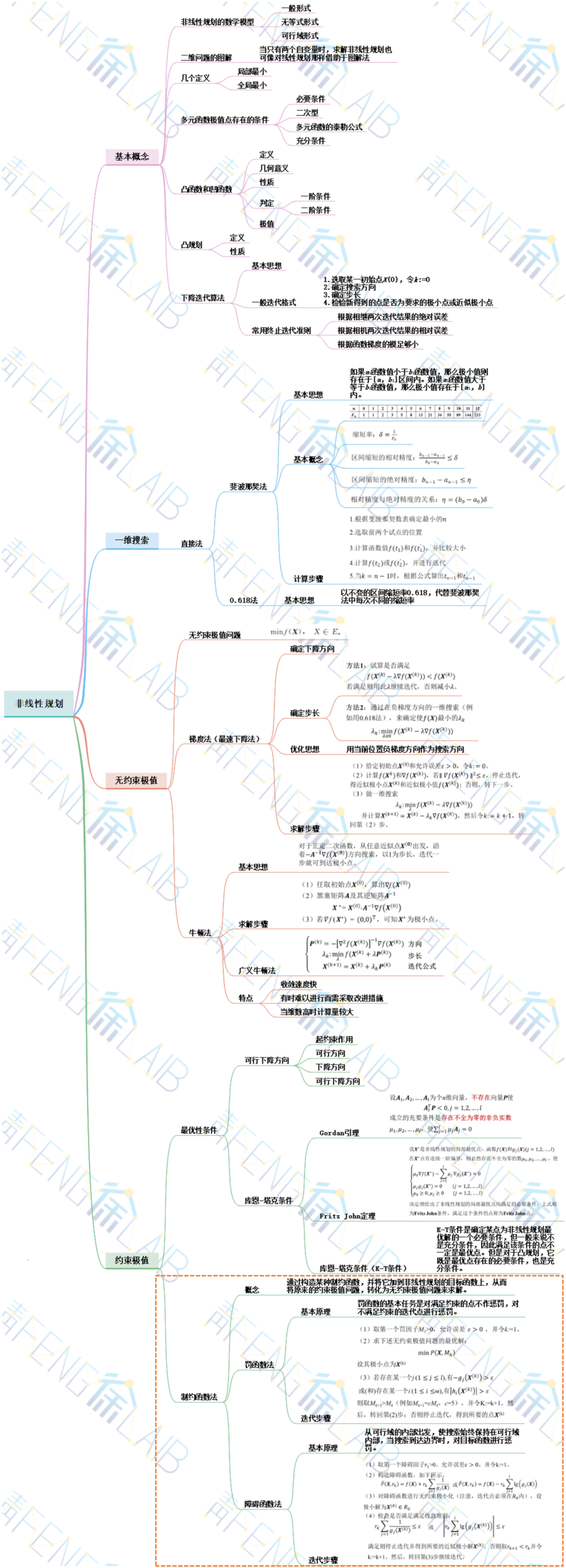
制约函数法是通过构造某种制约函数,并将它加到非线性规划的目标函数上,从而将原来的约束极值问题,转化为无约束极值问题来求解。此处介绍的方法用来求解一系列无约束问题,故称为序列无约束极小化技术。
一、罚函数法
对于非线性规划
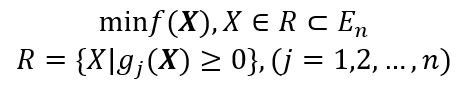
构造函数
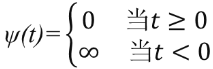
将视为t,将约束条件的函数加到原目标函数中,构造新的目标函数:
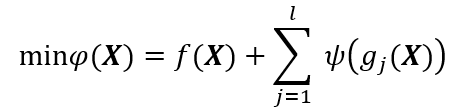
新的目标函数转变为求解无约束问题,假定该问题极小点为X*,必有,X*是新构造无约束问题的极小点,同样也是原非线性规划问题的极小点。
但是,如上构造的函数ψ(t)在0处不连续,不可导,这就无法使用很多有效的无约束极值极小化方法进行求解。因此将其修改为
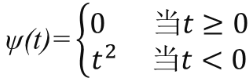
修改后的ψ(t)处处可导,ψ(t)和ψ′(t)处处连续。这时,修改后的函数的极小点不一定就是原非线性规划问题的极小点。于是,选取很大的实数M>0,作为惩罚因子,则得到
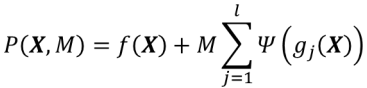
该式也可以写成另一种形式
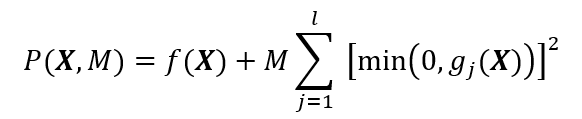
在这个式子中,M称为惩罚因子,为惩罚项,P(X,M)为罚函数。
当X∈R时,P(X,M)=P(X);当X∉R时,就会很大,离可行域越远,惩罚越大。当M足够大时,是新构造无约束问题的极小点,同样也是原非线性规划问题的极小点。
现引进阶跃函数
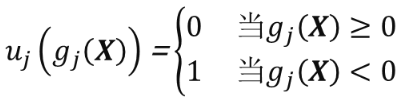
得到如下转变
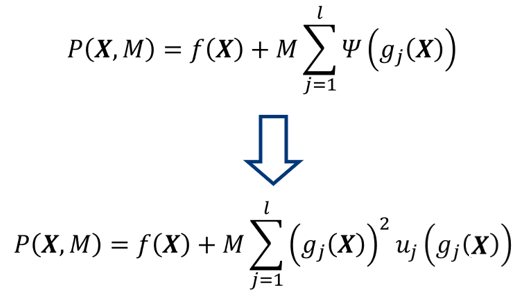
随着罚因子M增大,惩罚项起到的作用就越大,minP(X,M)越趋近于可行域,当0<M1<M2<...Mk<...,趋于无穷大时,点列
会从可行域R的外部趋于原非线性规划的问题的极小点(此处假设点列
收敛)。
和不等式约束问题类似,对于等式约束问题,也可做如下变换:

对于既含有等式约束,又有不等式约束的一般非线性规划问题
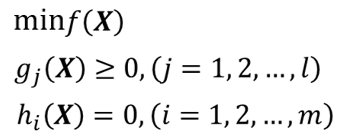
其罚函数为
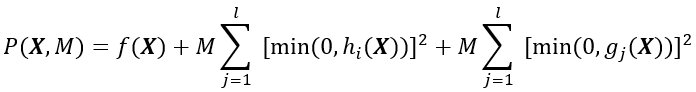
或
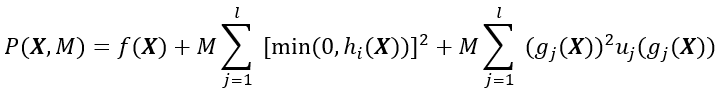
迭代步骤
(1)取第一个罚因子,允许ε>0,并令k:=1。
(2)求下述无约束极值问题的最优解:,设其极小点为
。
(3)若存在某一个j (1≤j≤l),有,或(和)存在某一个i (1≤i≤m),有
,则取
(例如
,c=5),并令K:=k+1。然后,转回第(2)步;否则停止迭代,得到所要的点
。
例题
用罚函数法求解
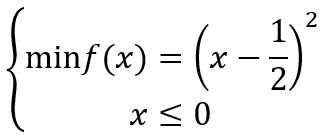
解:
(1)构造罚函数
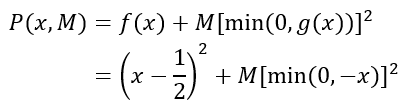
(2)对于固定的M,令
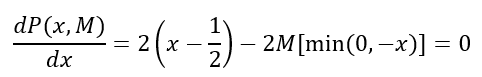
对于不满足约束条件的点x,有
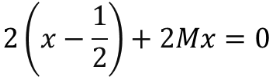
(3)求得其极小点x(M)为
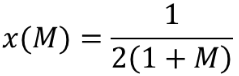
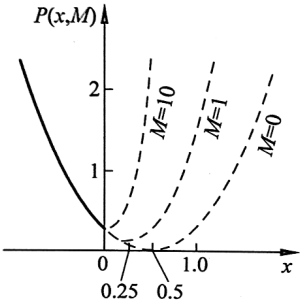
当M=0,x(M)=1/2
当M=1,x(M)=1/4
当M=10,x(M)=1/22
当M→∞,x(M)→0
因此,原约束问题的极小点x*=0
二、障碍函数法
对于罚函数而言,函数P(X,M)可在整个空间内进行优化,迭代过程往往在可行域外进行,不能以中间结果作为近似解使用。同时,目标函数在可行域外的性质比较复杂,甚至没有定义,就无法使用罚函数法。
障碍函数法与其不同,该方法要求迭代过程始终在可行域内进行。如果初始迭代点取在可行域内部(严格内点),在进行无约束极小化时,会阻止函数迭代到R的边界上,使迭代过程始终在可行域内部。此时的极小化是在不包括可行域边界的可行域开集上进行的,是一种具有无约束性质的极值问题,可用无约束极小化方法求解。
考虑非线性规划
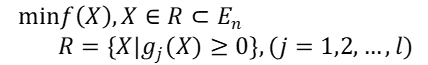
当X点从可行域R内部趋于边界时,至少有某一个约束函数(j=1,2,...,l)趋于0,从而得到倒数函数
以及(负)对数函数
都无限增大。
把倒数函数或对数函数加到目标函数上,则能构成新目标函数。取实数并构成一系列无约束性质的极小化问题如下:
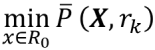
其中
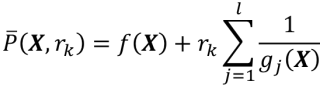
或
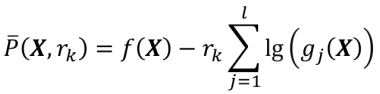
此处,为严格内点的集合,即
![]()
上述式子中,和
被称为障碍项,此处
为障碍因
,函数
为障碍函数。
若从某一点出发,按无约束极小化方法对问题进行迭代,随着障碍因子
减小,障碍项起到的作用越小,minP(X,M)求得的解会逐步逼近原约束问题的最小解。
因而,求得问题的解就会逐步逼近原约束问题的极小解。若原问题在可行域R的边界上,则随着
的减小,所求得障碍函数的极小点会不断靠近R的边界,直到满足某一精度要求时为止。
迭代步骤
(1)取第一个障碍因子,允许误差ε>0,并令k:=1。
(2)构造障碍函数,如下所示。
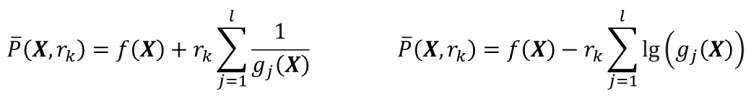
(3)对障碍函数进行无约束极小化(注意,迭代点必须在内),设极小解为
。
(4)检查是否满足收敛准则:
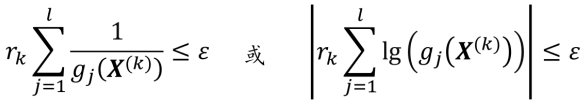
满足则停止迭代并得到所要的近似极小解。否则取
并令k:=k+1。然后,转回第(3)步继续迭代。
例题
用障碍函数法求解
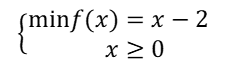
解:
(1)构造障碍函数
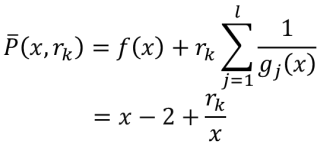
(2)对于固定的,由
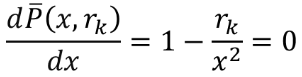
(3)求得其极小点x(r)为
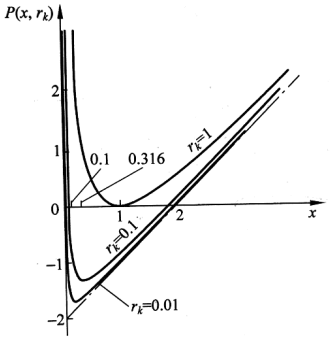
当r=1,x(r)=1
当r=0.1,x(r)=0.316
当r=0.01,x(r)=0.1
当r→0,x(r)→0
因此,原约束问题的极小点 x*= 0
初始内点迭代步骤
(1)任取一点,
,并令k:=1。
(2)确定指标集和
:
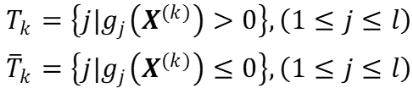
(3)检查是否为空集,若为空集,则取
为初始内点,停止迭代;否则,进行下一步。
(4)构造函数,将严格不等式不能满足的约束函数为假拟目标函数,严格满足的约束函数形成障碍项,构成一无约束性质问题,构造函数
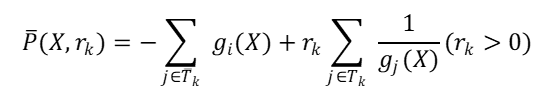
以为初始点,求解
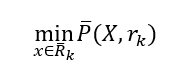
其中,
![]()
设求出的极小点,则
。令
,k:=k+1,转回第(2)步。
以上就是非线性规划中罚函数法与障碍函数法的全部内容了,通过本节学习大家是否对制约函数法有了一个大致的认识呢?到此为止,非线性规划的所有知识点就已经介绍完了,想要进一步了解运筹学,关注公众号运筹说,快快学起来吧!下期小编将为大家介绍与非线性规划相关的精品案例,敬请关注!
作者 |林若唯 唐京茹
责编 | 陈梦
审核 | 徐小峰

知乎 :运筹说
Bilibili :运筹说
CSDN :运筹说