Newton-Raphson Method

Linear vs Nonlinear Analysis:

• At this point, we can conduct a linear analysis no problem

$$\begin{array}{rl}& \int \sum _{i,j=1}^3{\sigma }_{ij}{\epsilon }_{ij}^{\ast }dv=\int t_n\cdot u^{\ast }ds+\int \rho b\cdot u^{\ast }dv\\ \Rightarrow & \underset{k_e}{\underbrace{{\int }_e[B{]}^T[C][B]dx}}{u}_e={\int }_{\partial e}[N{]}^T{t}_{n}ds+{\int }_e[N{]}^T\rho bdv\end{array}$$

• Two Assumption:

(1) Small Deformations
(2) Linear Elastic Materials

• This allowed us to solve our system using a system of linear equations:

$$\begin{array}{r}[K][u]=[F]\end{array}$$

• Unfortunately, the world is a cruel place and the majority of realistic scenarios require a nonlinear analysis:

Stress-Strain Relationship:
$$\begin{array}{rl}& \int \sum _{i,j=1}^3{\sigma }_{ij}{\epsilon }_{ij}^{\ast }dv\end{array}$$

$t_n$ and $\rho b$ are solution dependent:

$$\begin{array}{r}\int t_n\cdot u^{\ast }ds+\int \rho b\cdot u^{\ast }dv\end{array}$$

Types of Nonlinearities

There are many types of nonlinearities:

1. Geometric Nonlinearity

• Buckling
• Large deformation of the material
  

2. Material Nonlinearity

• Plasticity
• Damage

3. Kinematic Nonlinearity

• Contact

Newton-Raphson Method (Single Variable)

To solve nonlinear equations we typically employ the Newton-Raphson method (also referred to as Newton’s method). To see how this method works, let’s examine a single variable scenario:

If we hace a continuous function $f$, we can perform a Taylor series expansion:

$$\begin{array}{r}f(x^{(i+1)})\approx f(x^{(i)})+\frac{\partial f(x^{(i)})}{\partial x}(x^{(i+1)}-x^{(i)})+\frac{1}{2!}(\frac{{\partial }^{2}f(x^{(i)})}{\partial x^2})(x^{(i+1)}-x^{(i)})+...\end{array}$$

Neglecting higher-order terms:

$$\begin{array}{r}f(x^{(i+1)})\approx f(x^{(i)})+\frac{\partial f(x^{(i)})}{\partial x}(x^{(i+1)}-x^{(i)})\end{array}$$

Rearrange equation:

$$\begin{array}{rl}(x^{(i+1)}-x^{(i)})& =\frac{(f(x^{(i+1)})-f(x^{(i)}))}{f^{\prime }(x^{(i)})}\\ \Delta x& =(x^{(i+1)}-x^{(i)})\\ K_t& =f^{\prime }(x^{(i)})\end{array}$$

Simply equation:

$$\begin{array}{rl}\Delta x& =\frac{F-f(x^{(i)})}{K_t}=K_t^{-1}(F-f(x^{(i)}))\end{array}$$

Now let’s examine the parameters of the equation:

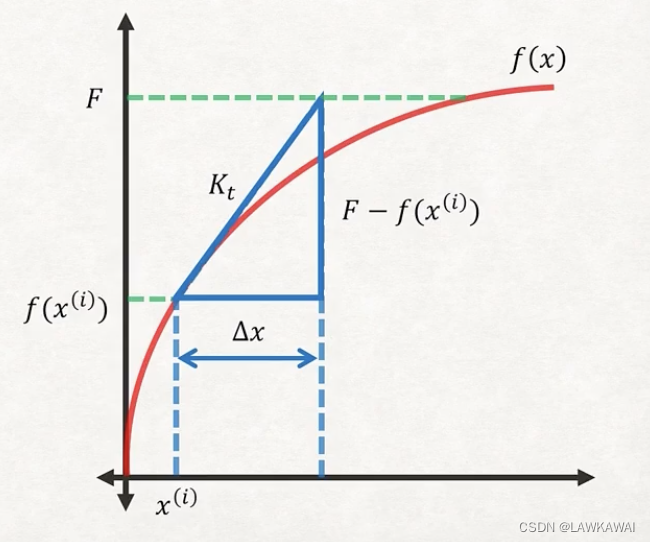
$F=$ Desired Value
$x^i=$ Initial Value of $x$
$f(x^{(i)})=$ Initial Value of the Function
$K_t=$ Slope of the Tangent Line
$\Delta x=$ Increment in $x$ : solve it

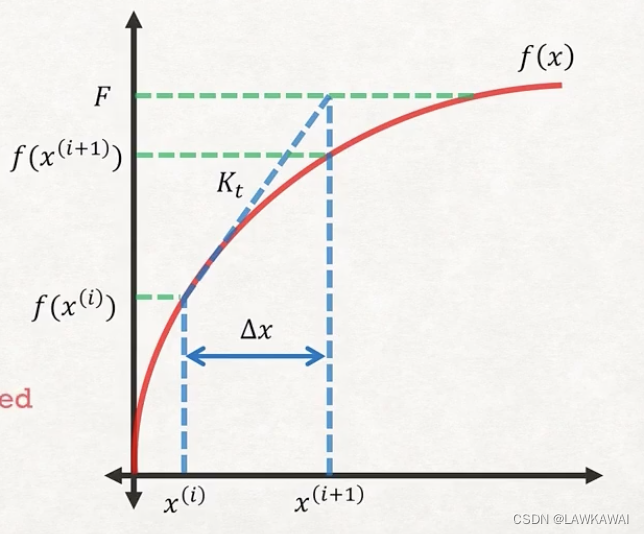
In FEA:

• $F-f(x^{(i)})=$ Different between applied forces $(F)$ and internal forces $(f(x^{(i)}))$
• $\Delta x=$ Displacement increment

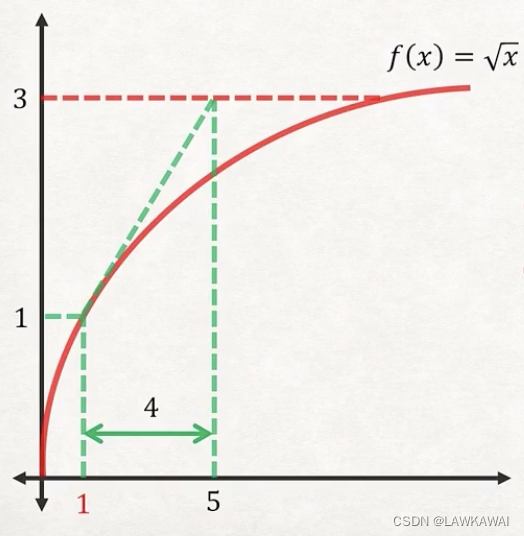
Example 1 - Single Variable Newton-Raphson Method

If $f(x)=\sqrt{x}$, find $x$ such that $f(x)=3$

Function Information:

$$\begin{array}{r}f(x)=\sqrt{x}\Rightarrow K_t=\frac{\partial f}{\partial x}=\frac{1}{2\sqrt{x}}\end{array}$$

$\Delta x=K_t^{-1}(F-f(x^{(i)}))$

$x^{(i)}$	$f(x^{(i)})$	$K_t$	$\Delta x$	$x^{(i+1)}$
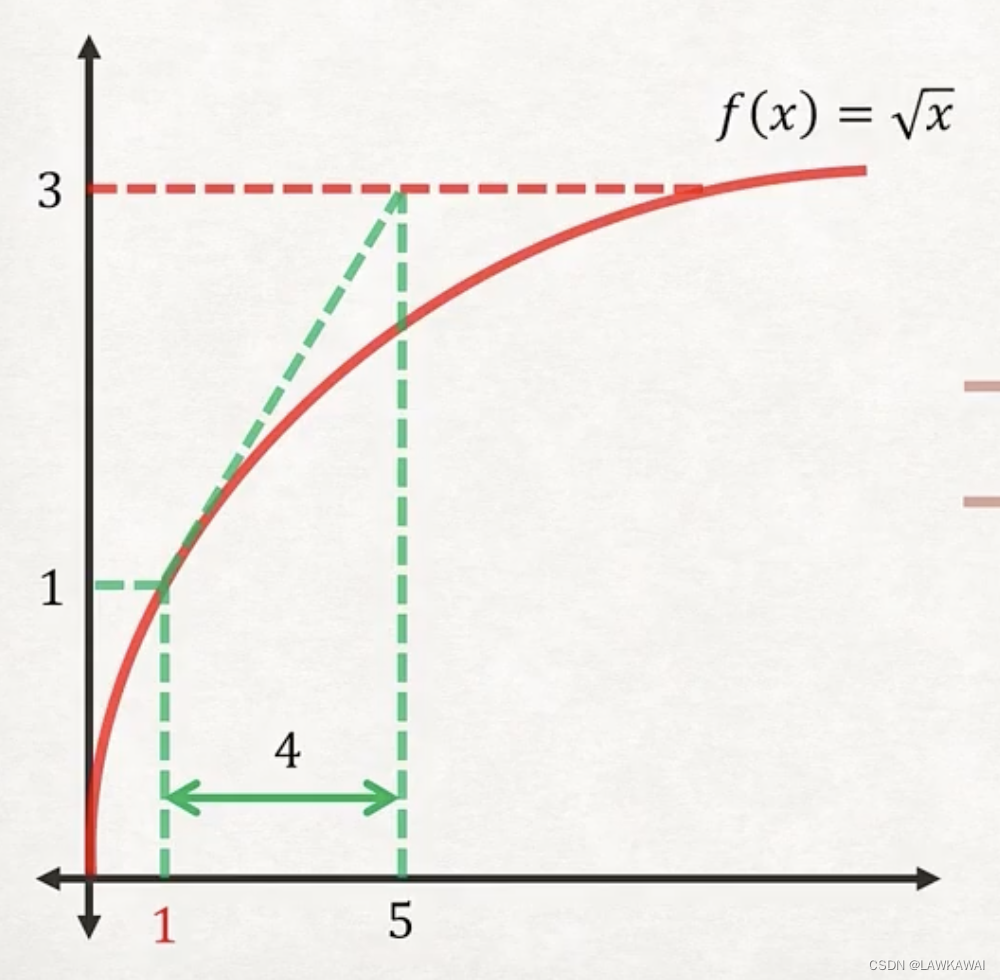
1	1	0.5	4	5

$\Delta x=K_t^{-1}(F-f(x^{(i)}))=(0.5{)}^{-1}(3-1)=4$

$x^{(i)}$	$f(x^{(i)})$	$K_t$	$\Delta x$	$x^{(i+1)}$
1	1	0.5	4	5
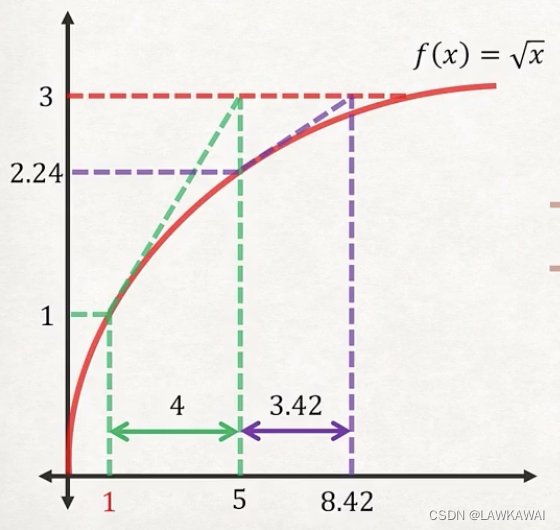
5	2.24	0.22	3.42	8.42

$x^{(i)}$	$f(x^{(i)})$	$K_t$	$\Delta x$	$x^{(i+1)}$
1	1	0.5	4	5
5	2.24	0.22	3.42	8.42
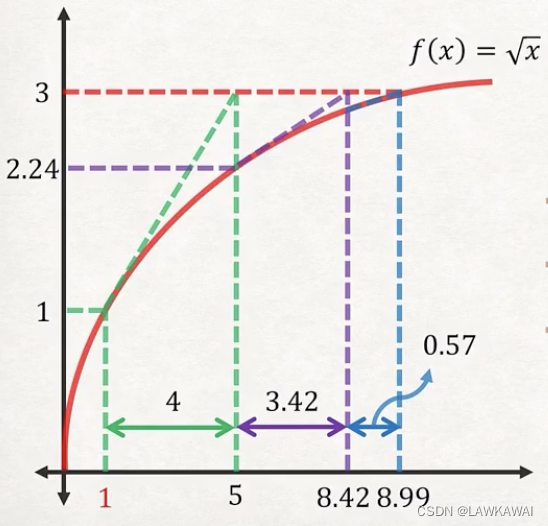
8.42	2.90	0.17	0.57	8.99

Newton-Raphson Method (Multi-Variable)

Unfortunately, most scenarios (especially finite element) involve many multi-variable equations:

$$\begin{gathered} f_1(x_1,x_2,...,x_n)=0 \\ {f}_2(x_1,x_2,...,x_n)=0 \\ ⋮ \\ {f}_n(x_1,x_2,...,x_n)=0 \end{gathered}$$

We can perform the Taylor series expansion for each equation:

$$\begin{array}{rl}& f_1(x_1^{(i+1)},x_2^{(i+1)},...,x_n^{(i+1)})\approx f_1(x_1^{(i)},x_2^{(i)},...,x_n^{(i)})\\ & +\frac{\partial f_1}{\partial x_1}{|}_{x^{(i)}}(x_1^{(i+1)}-x_1^{(i)})+\frac{\partial f_1}{\partial x_2}{|}_{x_2^{(i)}}(x^{(i+1)}-x_2^{(i)})+\cdots +\frac{\partial f_1}{\partial x_n}{|}_{x_n^{(i)}}(x^{(i+1)}-x_n^{(i)})\end{array}$$

Writing all the equations in matrix form:

$$\begin{array}{r}\left[\begin{array}{c}{f}_1(x^{(i+1)})\\ f_2(x^{(i+1)})\\ ⋮\\ f_n(x^{(i+1)})\end{array}\right]=\left[\begin{array}{c}{f}_1(x^{(i)})\\ f_2(x^{(i)})\\ ⋮\\ f_n(x^{(i)})\end{array}\right]+\left[\begin{array}{cccc}\frac{\partial f_1}{\partial x_1}& \frac{\partial f_1}{\partial x_2}& \cdots & \frac{\partial f_1}{\partial x_n}\\ \frac{\partial f_2}{\partial x_1}& \frac{\partial f_2}{\partial x_2}& \cdots & \frac{\partial f_2}{\partial x_n}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial f_n}{\partial x_1}& \frac{\partial f_n}{\partial x_2}& \cdots & \frac{\partial f_n}{\partial x_n}\end{array}\right]\left[\begin{array}{c}(x_1^{(i+1)}-x_1^{(i)})\\ (x_2^{(i+1)}-x_2^{(i)})\\ ⋮\\ (x_n^{(i+1)}-x_n^{(i)})\end{array}\right]\end{array}$$

We can move the vector containing the value of the functions at the initial guess to the other side to obtain the following:

$$\left[\begin{array}{cccc}\frac{\partial f_1}{\partial x_1}& \frac{\partial f_1}{\partial x_2}& \cdots & \frac{\partial f_1}{\partial x_n}\\ \frac{\partial f_2}{\partial x_1}& \frac{\partial f_2}{\partial x_2}& \cdots & \frac{\partial f_2}{\partial x_n}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial f_n}{\partial x_1}& \frac{\partial f_n}{\partial x_2}& \cdots & \frac{\partial f_n}{\partial x_n}\end{array}\right]\left[\begin{array}{c}(x_1^{(i+1)}-x_1^{(i)})\\ (x_2^{(i+1)}-x_2^{(i)})\\ ⋮\\ (x_n^{(i+1)}-x_n^{(i)})\end{array}\right]=\left[\begin{array}{c}{f}_1(x^{(i+1)})\\ f_2(x^{(i+1)})\\ ⋮\\ f_n(x^{(i+1)})\end{array}\right]-\left[\begin{array}{c}{f}_1(x^{(i)})\\ f_2(x^{(i)})\\ ⋮\\ f_n(x^{(i)})\end{array}\right]$$

or in a more simple form:

$$[K][\Delta x]=[F]-[f(x^{(i)})]$$

Moving $[K_t]$ to the other side:

$$[\Delta x]=[K_t{]}^{-1}([F]-[f(x^{(i)})])$$

Same as single variable case but now we have vectors and matrices

Convergence Checks:

With multiple variables it is difficult to determine if the method has converged or not. To make things easier, the norm of the vectors is used:

1. Force (and Moment) Convergence:

• Force convergence is achieved when the norm of the vector $f(x^{(i)})-F$ divided by the norm of vector $F$ is less than the specified tolerance $e_R$

$$\frac{||f(x^{(i)})-F||}{||F||}\le e_R$$

2. Displacement Convergence:

• Force convergence is achieved when the norm of the vector $\Delta u$ divided by the norm of vector $x^{(i)}$ is less than the specified tolerance $e_u$
  $$\frac{||\Delta x||}{||x^{(i)}||}\le e_e$$

Example 2 - Multi-Variable Newton-Raphson Method:

If $f(x_1,x_2)=[20x_1^4{x}_2+3x_2^3,20x_1^2{x}_2^3]$, find { x 1 , x 2 } \{x_1, x_2\} {x1​,x2​} such that $f(x_1,x_2)=[20,1]$

Function Information:

$$\begin{array}{rl}{f}_1(x_1,x_2)& =20x_1^4{x}_2+3x_2^3\\ f_2(x_1,x_2)& =20x_1^2{x}_2^3.\\ \Rightarrow [K_t]& =\left[\begin{array}{cc}\frac{\partial f_1}{\partial x_1}& \frac{\partial f_1}{\partial x_2}\\ \frac{\partial f_2}{\partial x_1}& \frac{\partial f_2}{\partial x_2}\end{array}\right]=\left[\begin{array}{cc}80x_1^3{x}_2& 20x_1^4+9x_2^2\\ 40x_1{x}_2^3& 60x_1^2{x}_2^2\end{array}\right]\end{array}$$

Sample Calculations ($1^{st}$ Iteration):
$$\begin{array}{rl}{f}_1(1,1)& =20(1{)}^4(1)+3(1{)}^3=23\\ f_2(1,1)& =20(1{)}^2(1{)}^3=20\\ [K_t]& =\left[\begin{array}{cc}80(1{)}^3(1)& 20(1{)}^4+9(1{)}^2\\ 40(1)(1{)}^3& 60(1{)}^2(1{)}^2\end{array}\right]\\ \Rightarrow [K_t]& =\left[\begin{array}{cc}80& 29\\ 40& 60\end{array}\right]\\ [\Delta x]& =[K_t{]}^{-1}([F]-[f])\\ [\Delta x]& ={\left[\begin{array}{cc}80& 29\\ 40& 60\end{array}\right]}^{-1}(\left[\begin{array}{c}20\\ 1\end{array}\right])-\left[\begin{array}{c}23\\ 20\end{array}\right])=\left[\begin{array}{c}0.102\\ -0.385\end{array}\right])\end{array}$$

$x_1^{(i)}$	$x_2^{(i)}$	$f_1(x^{(i)})$	$f_2(x^{(i)})$	$\Delta x_1$	$\Delta x_2$	$e_R$	$e_u$
1	1	23	20	0.102	-0.385	96.1	28.1
1.102	0.615	18.838	5.650	0.125	-0.215	23.9	19.7
1.227	0.400	18.325	1.927	0.096	-0.085	9.6	9.9
$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
1.348	0.302	19.979	1.001	0.001	-0.0001	0.1	0.04

6 Iterations

Other Methods:

Over the years the Newton-Raphson method has been modified to help improve stability and reduce computation time:

1. Modified Newton-Rapshson Method

• $[K_t]$ is recalculated at selected iterations (say every $5^{th}$ increment) or kept constant during the entire analysis
• Requires additional computations to converge but is able to reduce computation cost

Secant Method (Quasi-Newton)

• Approximates $[K_t]$ after the first iterations

$$[K_t{]}_i=\frac{f(x^{(i)})-f(x^{(i-1)})}{x^{(i)}-x^{(i-1)}}$$

• Don’t need to calculate derivatives!
• Provides a good convergence rate while reducing the computational cost

Example 3- Single Variable Modified Newton-Raphson Method:

If $f(x)=\sqrt{x}$, find $x$ such that $f(x)=3$

Function Information:

$$\begin{array}{r}f(x)=\sqrt{x}\Rightarrow K_t=\frac{\partial f}{\partial x}=\frac{1}{2\sqrt{x}}\end{array}$$

$\Delta x=K_t^{-1}(F-f(x^{(i)}))$

$x^{(i)}$	$f(x^{(i)})$	$K_t$	$\Delta x$	$x^{(i+1)}$
1	1	0.5	4	5

$x^{(i)}$	$f(x^{(i)})$	$K_t$	$\Delta x$	$x^{(i+1)}$
1	1	0.5	4	5
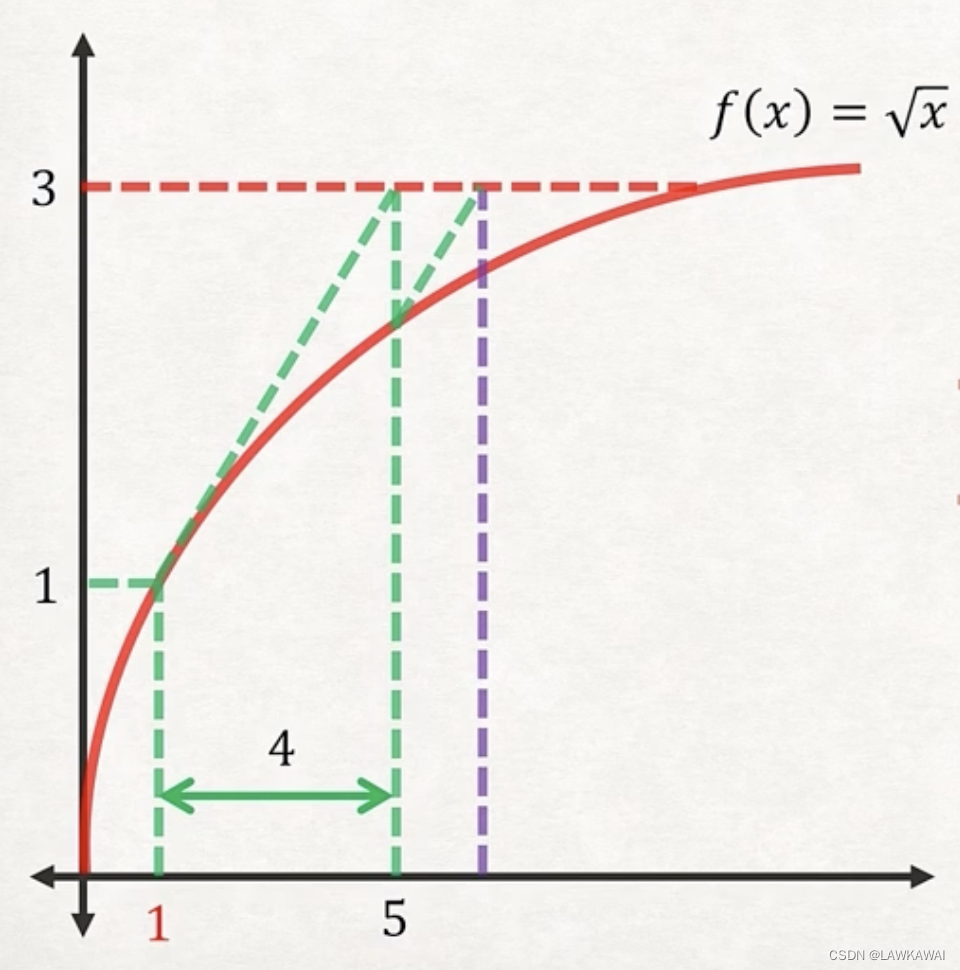
5	2.24	0.5	1.52	6.52

$x^{(i)}$	$f(x^{(i)})$	$K_t$	$\Delta x$	$x^{(i+1)}$
1	1	0.5	4	5
5	2.24	0.5	1.52	6.52
6.52	2.55	0.5	0.89	7.41

$x^{(i)}$	$f(x^{(i)})$	$K_t$	$\Delta x$	$x^{(i+1)}$
1	1	0.5	4	5
5	2.24	0.5	1.52	6.52
6.52	2.55	0.5	0.89	7.41
7.41	2.72	0.5	0.55	7.97

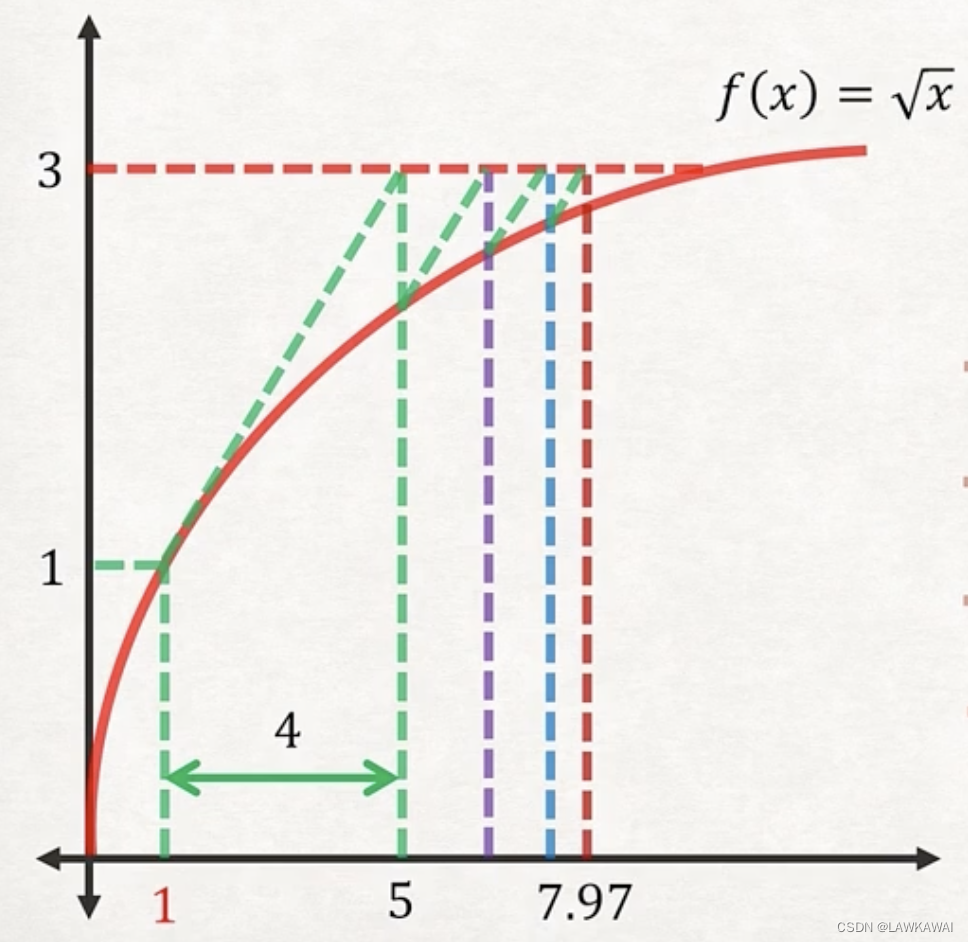
Slower Convergence!!

Material Nonlinearity Example

Wolfram Mathematica

(* Material Nonlinearity Example*)
 Clear["Global *"]
 
 (*Parameters *)  
 L = 1.0;
 A = 1;
 p = X1^2';

(* Newton-Raphson Parameters*)
Xi = 1;
ErrorLimit = 0.5;
MaxIter = 1;

(* Stress-Strain Relationship *)
s = 10 * u'[X1] + 100000 * u'[X1]^3;


(* Exact Solution *)
DE = D[s*A, X1]+p;
sol = NDSolve[{DE == 0, u[0] == 0, u[L] == 0}, u[X1], X1];   // Numerical  
uExact = u[X1] /. sol[[1]]; 

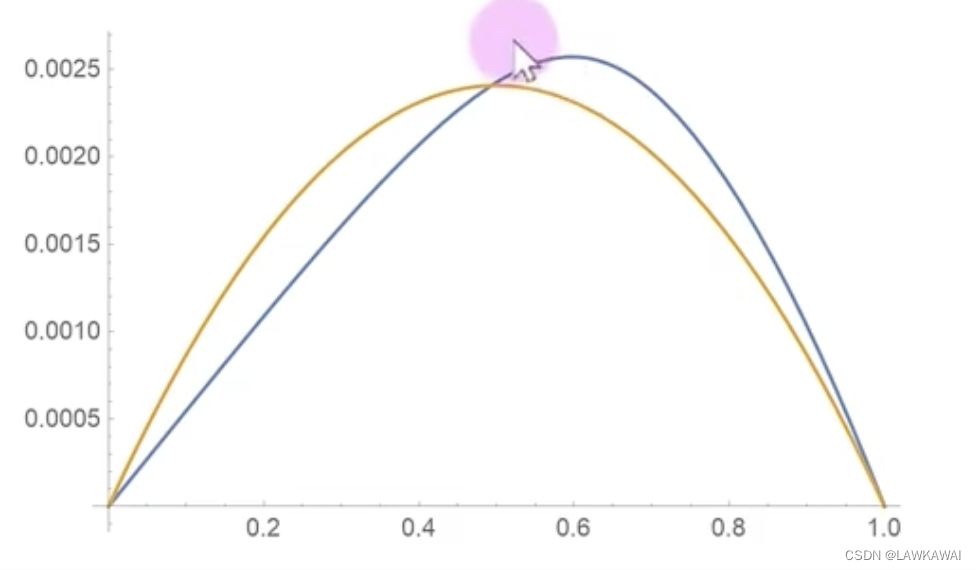
Plot[uExact, {X1, 0, L}]

(* RR Approximation *)



(* Approximation Function *)
uApprox = a0 + a1*X1 + a2*X1^2;

(* Essential Boundary Conditioons *)
BC1 = uApprox /. {X1 -> 0};
BC2 = uApprox /. {X1 -> L};
sol1 = Solve[{BC1 == 0, BC2 == 0}, {a0, a1}];
{a0, a1} = {a0, a1} /. sol1[[1]];

(* Total Internal Strain Energy *)
S = 10 * e + 100000 * e^3;
SED = Integrate[S, {e, 0, e}];      // 5e^2 + 25000e^4, Strain Energy Density
e = D[uApprox, X1];
TSE = Integrate[SED, {X1, 0, L}];  // 1.66667a2^2+5000 a2^4,   Total Strain Energy

(* Work *)
W = Integrate[p * uApprox, {X1, 0, L}];   // -0.05a2

(* Potential Energy *)
PE = TSE - W;             // 0.05a2 + 1.66667a2^2 + 5000a2^4

(* Newton-Rapshon Method *)
// What equation trying to solve?

ai = {a2};
Func = D[PE, a2];    // f(x)
Kt = D[Func, a2];    // f'(x)


For[i = 1, i <= maxIter, i++

(* Calculate Function and Kt at Current Iteration *)
FuncIter = Func /. {a2 -> Xi};
KtIter = Kt /. {a2 -> Xi};

(* Solving for Delta X *)
Delta = (-1) * FuncIter / KtIter;

(* Finding Xi for Next Iteration *)
XInit = Xi;
Xi = Xi + Delta;


(* Break Loop Once Convergence Occurs *)
Error. = (Delta / XInit) * 100;
If[Abs[Error] <= ErrorLimit, 
 Print["Analysis Converged!"];
 Print["     Coefficient a2 = ",  Xi];
 Print["    Error= ", Error, " (%)"];
 a2 = Xi;
 Conv = 1;
 Break[]];

(* Track Results *)
Print["  Iteration: ", i];
Print["  Coefficient a2 = ", Xi];
Print["Error = ", Error, "(%)"];

(* Error Message if Max Number of Iterations Reached *)
If[i==maxIter, 
  Print["Max of Number of Iterations Reached"]];



]

Plot[{uExact, uApprox}, {X1, 0, L}]