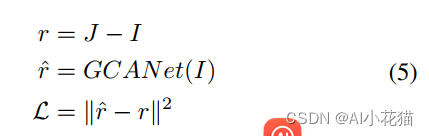邻接矩阵
- 表示方法:
- 优点:
- 缺点:
- 适用情况:
- 案例
- 代码
邻接矩阵是一种常见的图的存储结构,用于表示图中顶点之间的连接关系。它是一个二维数组,其中行和列分别表示图中的顶点,而数组中的值表示连接顶点之间的边或权重。邻接矩阵适用于表示稠密图,其中大部分顶点之间都有连接。
表示方法:
假设图中有n个顶点,那么邻接矩阵是一个n x n的矩阵。如果图是无向图且存在边(i, j),则矩阵中的第i行第j列和第j行第i列都会标记为1或表示边的权重值。对于有向图,矩阵中的元素表示从顶点i到顶点j的边或权重。
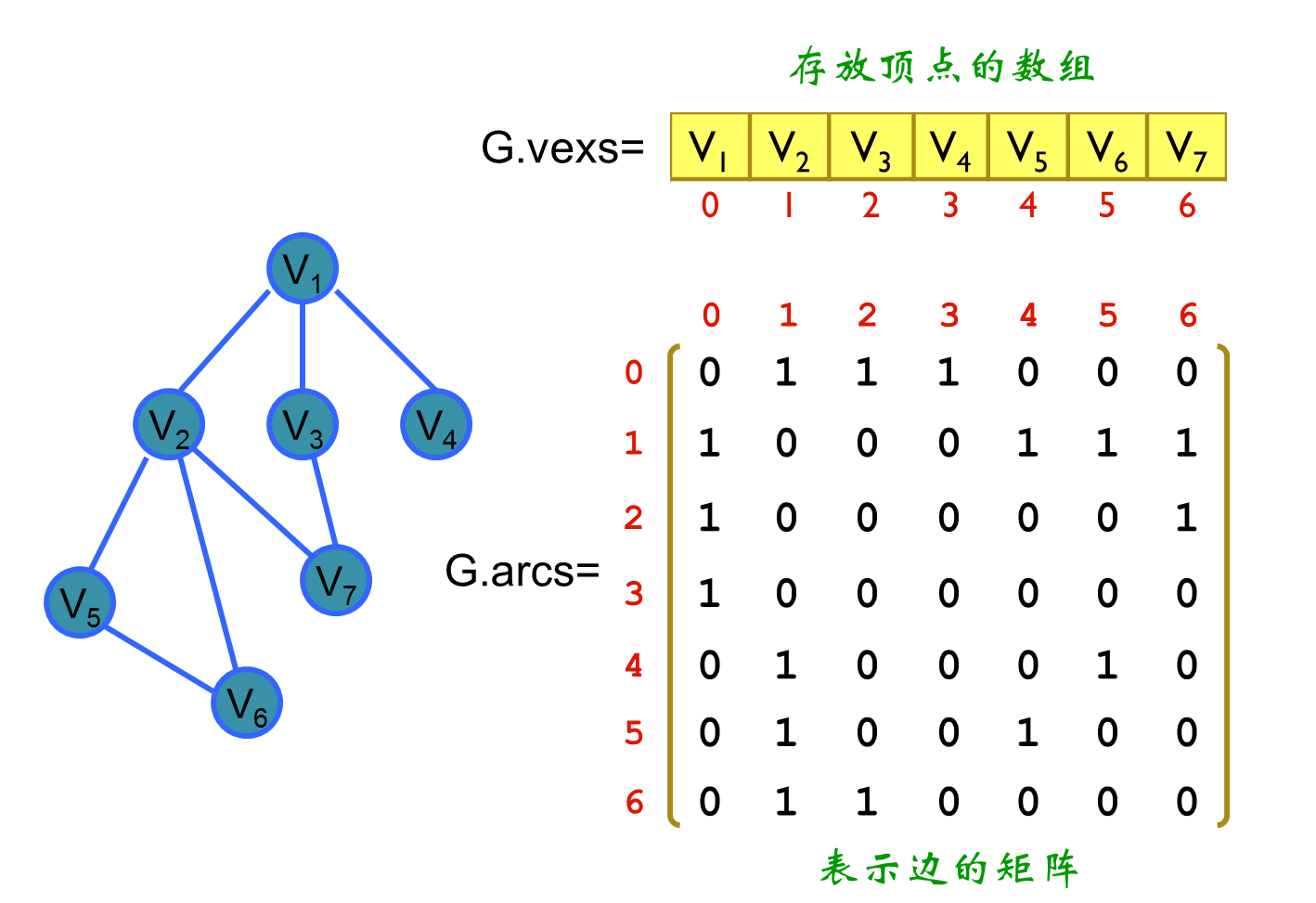
优点:
- 对于小规模的图,邻接矩阵可以提供快速的查找和更新操作。
- 判断任意两个顶点之间是否存在连接的边非常高效,只需访问对应的矩阵元素即可。
- 对于密集图,邻接矩阵比较节省存储空间,因为它只存储了实际存在的连接关系。
缺点:
- 对于稀疏图,邻接矩阵会浪费大量的存储空间,因为它需要存储许多不存在的边,这会增加存储开销。
- 当图中的顶点数非常大时,邻接矩阵可能会占用过多的内存空间。
- 在添加或删除顶点时,邻接矩阵的操作可能比较费时,因为它需要调整整个矩阵的结构。
适用情况:
邻接矩阵适用于静态图或者稠密图,其中大部分顶点之间都有连接。它特别适合用于快速查找和更新顶点之间的连接关系,以及执行基于矩阵的算法,比如矩阵运算和图论算法。然而,在面对稀疏图时,邻接矩阵可能不是最优的选择,因为它会浪费大量的存储空间。
案例
让我们以一个简单的无向图为例来说明邻接矩阵的概念。
考虑以下这个无向图:
(0)
/ \
/ \
/ \
(1)-----(2)
\ /
\ /
\ /
(3)
这个图有4个顶点和5条边。我们可以用邻接矩阵来表示这个图。假设顶点0到3分别表示矩阵的行和列,那么对应的邻接矩阵如下:
| 0 | 1 | 2 | 3 |
---|---|---|---|---|
0 | 0 | 1 | 1 | 0 |
1 | 1 | 0 | 1 | 1 |
2 | 1 | 1 | 0 | 1 |
3 | 0 | 1 | 1 | 0 |
在这个矩阵中,1表示对应的顶点之间有边相连,0表示没有边相连。因为这是一个无向图,所以邻接矩阵是对称的。例如,矩阵中的(0,1)和(1,0)、(1,2)和(2,1)的值都是1,表示顶点0和1之间、1和2之间有边相连。
使用邻接矩阵,我们可以快速查找任意两个顶点之间的连接关系,并进行图的遍历和其他算法操作。同时,这个矩阵表示了图的结构,使得图的分析和处理更加直观和方便。
代码
以下是Java中实现零阶矩阵的示例代码:
public class ZeroOrderMatrix {
private int[][] matrix;
// 构造函数用于初始化零阶矩阵
public ZeroOrderMatrix(int rows, int columns) {
matrix = new int[rows][columns];
}
// 获取矩阵行数
public int getRowCount() {
return matrix.length;
}
// 获取矩阵列数
public int getColumnCount() {
if (matrix.length > 0) {
return matrix[0].length;
}
return 0;
}
// 输出矩阵
public void printMatrix() {
for (int i = 0; i < getRowCount(); i++) {
for (int j = 0; j < getColumnCount(); j++) {
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
}
public static void main(String[] args) {
// 创建一个3行3列的零阶矩阵
ZeroOrderMatrix zeroOrderMatrix = new ZeroOrderMatrix(3, 3);
// 输出矩阵
zeroOrderMatrix.printMatrix();
}
}
运行这段代码将输出一个3行3列的零阶矩阵:
0 0 0
0 0 0
0 0 0
您可以根据需要对代码进行调整和扩展。