Hi， 你好。我是茶桁。

上一节课，我们从一个波士顿房价的预测开始写代码，写到了KNN。

之前咱们机器学习课程中有讲到KNN这个算法，分析过其优点和缺点，说起来，KNN这种方法比较低效，在数据量比较大的时候就比较明显。

那本节课，我们就来看一下更加有效的学习方法是什么，A more Efficient Learning Way.

接着我们上节课的代码我们继续啊，有不太了解的先回到上节课里去看一下。

我们X_rm和y如果能够找到这两者之间的函数关系，每次要计算的时候，输入给这个函数，就能直接获得预测值。

那这个函数关系怎么获得呢？我们需要先观察一下，这个时候就到了我们的拟合函数关系。

那既然要观察，当然最好就是将数据可视化之后进行观察：

import matplotlib.pyplot as plt
plt.scatter(X_rm, y)

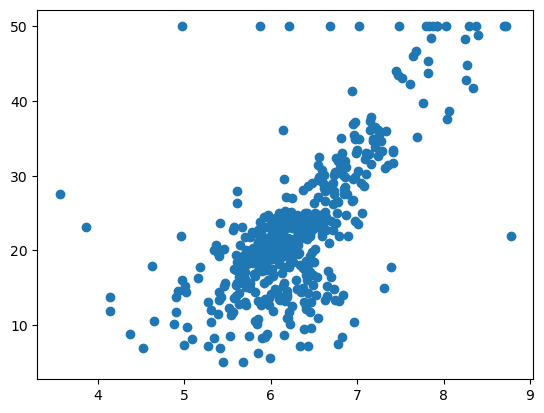
可以看到，它们之间的关系大体应该这样一种关系：

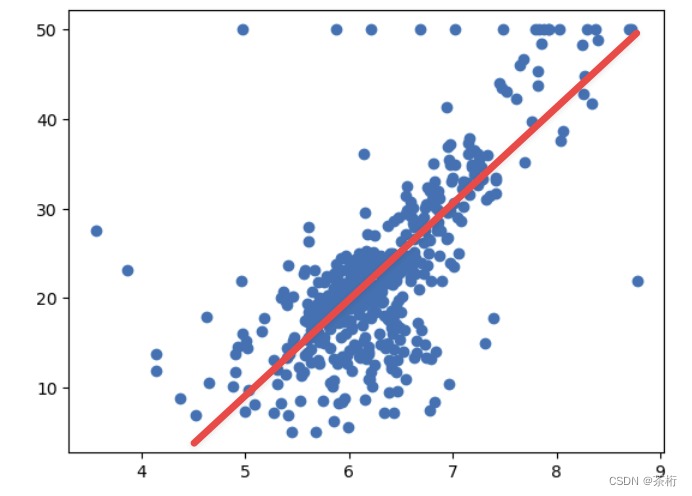
那这个样子的图我们熟悉不？ 是不是在线性回归那一张里我们见过？也就是用一根直线去拟合了这些点的一个趋势。

我们把它写出来：

$$f(x)=k\cdot rm+b$$

那我们现在就会把这个问题变成，假设现在的函数k*rm+b， 那我们就需要找到一组k和b，然后让它的拟合效果最好。这个时候我们就会遇到一个问题，拟合效果怎样算是好？

比方说我们现在有一组数据，一组实际的值，还有一组预测值。

real_y = {3, 6, 7}
y_hats = {3, 4, 7}
y_hats2 = {3, 6, 6}

问哪个值更好。

我们会发现这两个预测都挺好的，那哪个更好？这个时候我们需要搬出我们的loss函数了。

loss函数就是在我们进行预测的时候，它的信息损失了多少，所以我们称其为损失函数，loss函数。
$$loss(y,\hat{y})=\frac{1}{N}\sum _{i\in N}(y_i-\widehat{y_i}{)}^2$$
y_i - yhat_i这个值越接近于0。 等于0的意思就是每一个预测的y都和实际的y的值是一样的。那么如果这个值越大指的是预测的y和实际的y之间差的越大。

那我们在这个地方就可以定义一个函数：

def loss(y, yhat):
    return np.mean((np.array(y) - np.array(yhat))** 2)

然后我们直接将两组yhat和真实的real_y代入进去比对：

loss(real_y, y_hats)
loss(real_y, y_hats2)

---
1.3333333333333333
0.3333333333333333

所以它这个意思是说yhats2的效果更好一些。

那我们将上面这个loss函数就叫做Mean Squared Error，就是均方误差，也简称MSE。咱们现在有了loss，就有了是非判断的标准了，就可以找到最好的结果。

有了判断标准怎么样来获得最优的k和b呢？早些年的时候有这么几种方法，第一种是直接用微积分的方法做计算。
$$\begin{array}{rl}loss& =\frac{1}{N}\sum _{i\in N}(y_i-\hat{y}{)}^2\\ & =\frac{1}{N}\sum _{i\in N}(y_i-(k{x}_i+b){)}^2\end{array}$$
此时我们是知道x_i 和y_i的值，N也是常数。那么其实求偏导之后它就可以变化成下面这组式子：
$$\begin{gathered} A{k}^2+Bk+C \\ {A}^{\prime }{b}^2+B^{\prime }b+C^{\prime } \end{gathered}$$
A、B、C是根据我们所知道的x_i和y_i以及常数N来计算出来的数。这个时候loss要取极值的时候，我们令其为loss’， 那loss’就等于-A/2B，或者-A’/2B’。那么这种方法我们就称之为最小二乘法，它是为了最小化MSE，对MSE求偏导数并令其等于零，来找到使MSE最小的参数值。

但是为什么后来人们没有用微积方的方法直接做呢？是因为这个函数会变得很复杂，当函数变得极其复杂的时候,学过微积分的同学就应该知道，你是不能直接求出来他的导数的。也就是说当函数变得极其复杂的时候，直接用微积分是求不出来极致点的，所以这种方法后来就没用。

第二种方法，后来人们想了可以用随机模拟的方法来做。

我们首先来在-100到100之间随机两个值：k和b

VAR_MAX, VAR_MIN = 100, -100
k, b = random.randint(VAR_MIN, VAR_MAX), random.randint(VAR_MIN, VAR_MAX)

只拿到一组当然是无从比较的，所以我们决定拿个100组的随机值：

total_times = 100
for t in range(total_times):
    k, b = random.randint(VAR_MIN, VAR_MAX), random.randint(VAR_MIN, VAR_MAX)

然后定义一个值, 叫做最小的loss。这个最小的loss一开始取值为无穷大，并且再给两个值，最好的k和最好的b，先赋值为None

min_loss = float('inf')
best_k, best_b = None, None

之后我们要拿预测值来赋值给新的loss，我们来定义一个函数，它要做的事情很简单，就是返回k*x+b

def model(x, k, b):
    return k*x + b

loss_ = loss(y, model(X_rm, k, b))

接着我们就可以来进行对比了，就会找到那组最好的k和b：

if loss_ < min_loss:
    min_loss = loss_
    best_k, best_b = k, b

完整的代码如下， 当然我们是接着之前的代码写的，所以loss函数和y，还有X_rm都是在之前代码中有过定义的。

VAR_MAX, VAR_MIN = 100, -100
min_loss = float('inf')
best_k, best_b = None, None

def model(x, k, b):
    return x * k +b

total_times = 100

for t in range(total_times):
    k, b = random.randint(VAR_MIN, VAR_MAX), random.randint(VAR_MIN,VAR_MAX)

    loss_ = loss(y, model(X_rm, k, b))

    if loss_ < min_loss:
        min_loss = loss_
        best_k, best_b = k, b
        print("在{}时刻找到了更好的k: {}, b: {}， 这个loss是：{}".format(t, k, b, loss_))

---
在0时刻找到了更好的k: 12, b: 89， 这个loss是：20178.46882444269
在8时刻找到了更好的k: 2, b: 2， 这个loss是：131.87000511462452
在21时刻找到了更好的k: 11, b: -48， 这个loss是：47.340357088932805

如果我们将寻找的次数放大，改为10**3, 那我们会发现，开始找的很快，但是后面寻找的会越来越慢。

就类似于你现在在一个公司，假设你从刚进去的时候，要达到职位很高，薪水很高。小职员你想一直升职，你可以随机的去做很多你喜欢做的事情，没有人指导你。一开始的时候，你会发觉自己的升职加薪似乎并没有那么困难，但是随着自己越往上，升职的速度就降下来了，因为上面职位并没有那么多了。这个时候你所需要尝试和努力就会越来越多。到后面你每尝试一步，你所需要的努力就会越来越多。

那么这个时候我们就要想，我们怎么样能够让更新频率更快呢？而不要像这样到后面基本上不更新了。

不知道我们是否还记得大学时候的数学知识，假设现在这个loss和k在一个二维平面上，我们对loss和k来求一个偏导:

$$\frac{\partial loss}{\partial k}$$

这个导数的取值范围就会导致两种情况，当其大于0的时候，k越大，则loss也越大，当其小于0的时候，k越大，loss则越小。

那我们在这里就可以总结出一个规律：

$$p^{\prime }=p+(-1)\frac{\partial loss}{\partial p}\ast \alpha$$

$\alpha$就是一个很小的数，因为我们每次要只能移动很小的一点，不能减小很多。

那有了这个，我们就可以将我们的k和b应用上去，也就可以得到：

$$\begin{array}{r}{k}^{\prime }=k+(-1)\frac{\partial loss}{\partial k}\cdot \alpha \\ b^{\prime }=b+(-1)\frac{\partial loss}{\partial b}\cdot \alpha \end{array}$$

那我们如何使用计算机来实现刚刚讲的这些内容呢？我们先把上面的式子再做一下变化：

$$\begin{gathered} k_{n+1}=k_n+-1\cdot \frac{\partial loss(k,b)}{\partial k_n} \\ {b}_{n+1}=b_n+-1\cdot \frac{\partial loss(b,b)}{\partial b_n} \end{gathered}$$

这个就是所谓的梯度下降。

那现在的问题就变成，如何使用计算机来实现梯度下降。我们就来定义两个求导函数，并且将之前的代码拿过来做一些修改：

def loss(y, yhat):
    return np.mean((np.array(y) - np.array(yhat)) ** 2)

def partial_k(x, y, k_n, b_n):
    return 2 * np.mean((y - (k * x + b))*(-x))

def partial_b(x, y, k_n, b_n):
    return 2 * np.mean((y - (k * x + b))*(-1))

k,b = random.random(), random.random()

min_loss = float('inf')
best_k, best_b = None, None

total_times = 500
alpha = 1e-3

k_b_history = []

for t in range(total_times):
    k = k + (-1) * partial_k(X_rm, y, k, b) * alpha 
    b = b + (-1) * partial_b(X_rm, y, k, b) * alpha

    loss_ = loss(y, model(X_rm, k, b))

    if loss_ < min_loss:
        min_loss = loss_
        best_k, best_b = k, b
        k_b_history.append([best_k, best_b])
        print("在{}时刻找到了更好的k: {}, b: {}， 这个loss是：{}".format(t, k, b, loss_))

---
在0时刻找到了更好的k: 0.8391888851738278, b: 0.44333100376779605， 这个loss是：360.000103176194
在1时刻找到了更好的k: 1.0586893752129705, b: 0.474203003102507， 这个loss是：312.7942150454931
...
在498时刻找到了更好的k: 3.587603582169745, b: 0.40777844839877003， 这个loss是：58.761172062586965
在499时刻找到了更好的k: 3.587736446932306, b: 0.4069332804559017， 这个loss是：58.760441520932375

其实关于这个内容，我们在机器学习 - 线性回归那一章就介绍过。看不懂这一段的小伙伴可以回过头取好好看一下那一章。

那这样，我们可以发现，之前是间隔很多次才作一词更新，而现在是每一次都会进行更新，一直在减小。这个是因为我们实现了一个「监督」。

在这样的情况下结果就变得更好了，比如我们再将次数调高一点，在全部运行完之后，我们来画个图看看：

plt.scatter(X_rm, y)
plt.scatter(X_rm, best_k * X_rm + best_b, color='orange')
plt.plot(X_rm, best_k * X_rm + best_b, color='red')

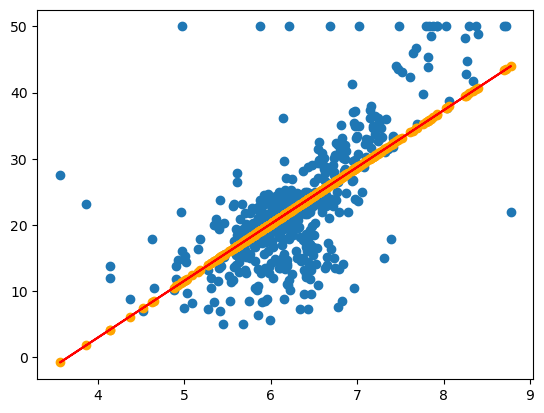
我们可以看到它拟合出来的点和连接成的直线，和我们上面手动去画的似乎还是有很大差别的。

在刚才的代码里我还做了一件事情，定义了一个k_b_history, 然后将所有的best_k和best_b都存储到了里面。然后我们随机取几个点，第一个取第10个测试点，第二个取第50次测试点，第三个我们取第5000次，第四个我们取最后一次:

test_0, test_1, test_2, test_3, test_4 = 0, 10, 50, 5000, -1

然后我们分别画一下这几个点的图：

plt.scatter(X_rm, y)
plt.scatter(X_rm, k_b_history[test_0][0] * X_rm + k_b_history[test_0][1])
plt.scatter(X_rm, k_b_history[test_1][0] * X_rm + k_b_history[test_1][1])
plt.scatter(X_rm, k_b_history[test_2][0] * X_rm + k_b_history[test_2][1])
plt.scatter(X_rm, k_b_history[test_3][0] * X_rm + k_b_history[test_3][1])
plt.scatter(X_rm, k_b_history[test_4][0] * X_rm + k_b_history[test_4][1])

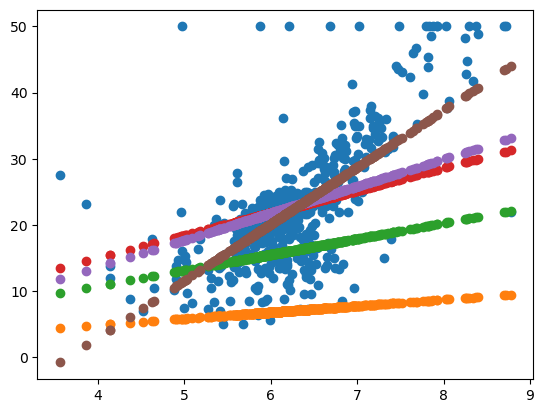
我们就可以看到，刚开始的时候和最后的一次拟合的线的结果，还有中间一步步的拟合的变化。这条线在往上面一步一步的走。这样我们相当于是透视了它整个获得最优的k和b的过程。

那这个时候我们来看一下，咱们怎么怎么预测呢？我们可以拿我们的best_k和best_b去输出最后的预测值了：

model(7, best_k, best_b)

---
28.718752244698216

预测出来是28.7万。那房间数目为7的时候，我们预测出这个价格是28.7万，还记得咱们上节课中用KNN预测出来的值么？

find_price_by_simila(rm_to_price, 7)

---
29.233333333333334

是29万对吧？现在我们就能看到了，这两种方式预测值基本很接近，都能预测。

那么我们使用函数来进行预测的原因还有一个，就是我们在使用函数在进行学习之后，然后拿模型去计算最后的值，这个计算过程速度会快很多。

好，咱们下节课将会学习怎样拟合更加复杂的函数，因为这个世界上的函数可不仅仅是最简单线性，还得拟合更加复杂的函数。

然后再后面的课程，我们会讲到激活函数，开始接触神经网络，什么是深度学习。

然后我们要来讲解一个很重要的概念，就是反向传播，会讲怎么样实现自动的反向传播。实现了自动的反向传播，我们会基于拓普排序的方法让计算机能够自动的计算它的梯度和偏导。

在讲完这些之后，基本上我们就有了构建一个深度学习神经网络框架的内容了。

好，希望小伙伴们在今天的课程中有所收获。