LeetCode51. N 皇后
题目链接:51. N 皇后
题目描述:
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
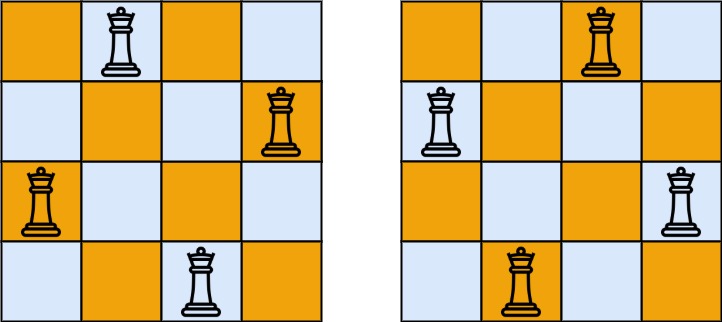
输入:n = 4 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] 解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1 输出:[["Q"]]
提示:
1 <= n <= 9
算法分析:
首先我们创建一张字符串数组ArrayList<StringBuffer> path2来描述整张棋盘(因为后面需要对棋盘上地每个格子进行操作也即字符串中的元素,所以我们用StringBuffer来当作数组元素),然后用"."来填充棋盘上地每个格子。
然后通过递归一层一层的去遍历棋盘(path),然后放置皇后"Q";
递归结束条件:当放置到最后一层时,说明已经有一种放置方法了,将这种解法放置到结果及当中。
代码如下:
public void backTravel(int startx) {//递归时,向下一层一层地放置皇后
if(startx == len) {//如果最后一层也放了皇后,说明有一种解法了。
//将path2先转化成String再,将其放到结果集
....
return;
}
}然后在每一层当中,从左到右一次去遍历,并判断该位置是否可以放皇后,如果可以放置,将当前位置的字符修改为"Q",然后递归下一层,在回溯:
for(int j = 0; j < len; j++) {//每一层,从左到右遍历,并判断该位置是否可以放置皇后
if(canPut(startx, j) == true) {
... //如果可以放置,将当前位置地字符'.'修改成'Q';
...//递归,去放置下一层
...//回溯
}
}判断当前是否可以放置皇后的方法:
public boolean canPut(int x, int y) {//用来判断坐标位置是否可以放上皇后
for(int j = y; j < len; j++) {//向左搜索是否有皇后,因为还没对右边操作过所以不用遍历
....
return false;
}
for(int i = x; i >= 0; i--) {//向上搜索是否幽皇后,因为还没对下边进行操作所以不用遍历
.....
return false;
}
for(int i = x - 1, j = y - 1; i >= 0 && j >= 0; i--, j--) {//向左上对角线遍历是否有皇后
.....
return false;
}
for(int i = x - 1, j = y + 1; i >=0 && j < len; i--, j++) {//向右上对角线遍历是否有皇后
.....
return false;
}
//如果左边,右边,左上对角线,右上对角线都没有皇后说明可以在当前位置放置皇后,返回true
return true;
}完整的代码如下:
class Solution {
List<List<String>>result = new ArrayList<>();//用来收集所有的解法
ArrayList<StringBuffer>path = new ArrayList<>();//用来遍历每种解法,因为要对每个字符串中的字符进行修改操作,所以用StringBuffer
int len;//矩形边长
public boolean canPut(int x, int y) {//迎来判断坐标位置是否可以放上皇后
for(int j = y; j < len; j++) {//向左搜索是否有皇后,因为还没对右边操作过所以不用遍历
if(path.get(x).charAt(j) == 'Q')
return false;
}
for(int i = x; i >= 0; i--) {//向上搜索是否幽皇后,因为还没对下边进行操作所以不用遍历
if(path.get(i).charAt(y) == 'Q')
return false;
}
for(int i = x - 1, j = y - 1; i >= 0 && j >= 0; i--, j--) {//向左上对角线遍历是否有皇后
if(path.get(i).charAt(j) == 'Q')
return false;
}
for(int i = x - 1, j = y + 1; i >=0 && j < len; i--, j++) {//向右上对角线遍历是否有皇后
if(path.get(i).charAt(j) == 'Q')
return false;
}
//如果左边,右边,左上对角线,右上对角线都没有皇后说明可以在当前位置放置皇后,返回true
return true;
}
public void backTravel(int startx) {//递归时,向下一层一层地放置皇后
if(startx == len) {//如果最后一层也放了皇后,说明有一种解法了。
//将path2先转化成String再,将其放到结果集
ArrayList<String>path2 = new ArrayList<>();
for(StringBuffer sb : path) {
path2.add(sb.toString());
}
result.add(path2);
return;
}
for(int j = 0; j < len; j++) {//每一层,从左到右遍历,并判断该位置是否可以放置皇后
if(canPut(startx, j) == true) {
//如果可以放置,将当前位置地字符'.'修改成'Q';
path.get(startx).setCharAt(j, 'Q');
backTravel(startx + 1);//递归,去放置下一层
path.get(startx).setCharAt(j, '.');//回溯
}
}
}
public List<List<String>> solveNQueens(int n) {
len = n;
for(int i = 0; i < n; i++) {//将path2填充上'.';
StringBuffer sb = new StringBuffer();
for(int j = 0; j < n; j++)
sb.append(".");
path.add(sb);
}
backTravel(0);
return result;
}
}总结
这道题的难点是如何用字符来描述棋盘,并对每个格子进行是否可以放置皇后的判断和操作。
然后是放置皇后的顺序,我们用递归从上往下一层一层去遍历,每一层当中要从左到右一个个位置判断并放置皇后(注意回溯,每一层只能放一个)。