目录
一、数据及分析对象
二、目的及分析任务
三、方法及工具
四、数据读入
五、数据理解
六、数据准备
七、模型构建
八、模型预测
九、模型评价
一、数据及分析对象
CSV格式的数据文件——“Advertising.csv”
数据集链接:https://download.csdn.net/download/m0_70452407/88520033
数据集包含了200个不同市场的产品销售额,每个销售额对应3中广告媒体投入成本,分别是TV、radio和newspaper,主要属性如下:
(1)Number:数据集的编号。
(2)TV:电视媒体的广告投入。
(3)radio:广播媒体的广告投入。
(4)newspaper:报纸媒体的广告投入。
(5)sales:商品的销量。
二、目的及分析任务
理解机器学习方法在数据分析中的应用——采用多元回归方法进行回归分析。
(1)数据预处理,绘制TV、radio、newspaper这3个自变量与因变量sales的相关关系图。
(2)采用两种不同方法进行多元回归分析——统计学方法和机器学习方法。
(3)进行模型预测,得出模型预测结果。
(4)对预测结果进行评价。
三、方法及工具
Python语言及pandas、Seaborn、matplotlib、statsmodels、scikit-learn等包。
四、数据读入
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import os
data=pd.read_csv("D:\\Download\\JDK\\数据分析理论与实践by朝乐门_机械工业出版社\\第3章 回归分析\\Advertising.csv")
data.head()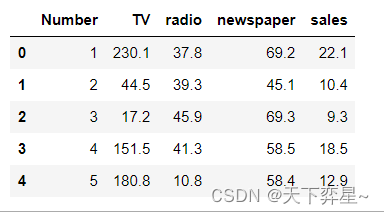
五、数据理解
对数据框进行探索性分析,这里采用的实现方式为调用Seaborn包中的pairplot()方法,绘制TV、radio、newspaper这3个变量与sales变量之间的关系图,其中kind参数设置为“reg"。为非对角线上的散点图拟合出一条回归直线,可以更直观地显示变量之间的关系,height参数为7,aspect参数为0.8,表明每个构面的高度为7,宽高比为0.8。调用matplotlib.pyplot.show()方法显示图形。
sns.pairplot(data,
x_vars=['TV','radio','newspaper'],
y_vars='sales',
height=7,
aspect=0.8,
kind='reg')
plt.show()
六、数据准备
进行多元回归分析前,应准备好模型所需的特征矩阵(X)和目标向量(y)。这里采用drop()方法删除数据框data中的Number以及sales两列返回另一个DataFrame对象Data,并显示Data数据集,即特征矩阵的前5行数据。
#第一步:构建特征矩阵和目标数组
Data=data.drop(['Number','sales'],axis=1)
Data.head()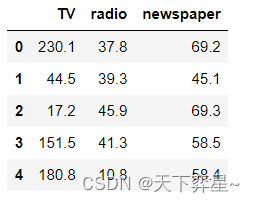
确定目标向量sales为data数据框中的sales列,并显示其数据类型:
sales=data['sales']
type(sales)pandas.core.series.Series
输出结果显示了sales的数据类型为pandas的Series。
将目标向量sales的数据转换为NumPy中的ndarray,这里采用的实现方法为调用NumPy包中的ravel()方法返回数组。
import numpy as np
sales=np.ravel(sales)
type(sales)numpy.ndarray
输出结果显示sales的数据类型为NumPy的ndarray数组对象。
七、模型构建
采用统计学方法,检验模型的线性显著性。在这里调用statsmodels统计建模工具包,通过statsmodels.api(基于数组)接口进行访问。采用add_constant()方法加上一列常数项,反映线性回归模型的截距。采用OLS()方法用最小二乘法来建立myModel模型。采用模型的fit()方法返回一个回归结果对象results,该对象results包含了估计的模型参数和其他的诊断。在results上调用summary()方法可以打印出一个模型的诊断细节。
#第一种分析方法——基于统计学的建模
import statsmodels.api as sm
X_add_const=sm.add_constant(Data.to_numpy())
myModel=sm.OLS(sales,X_add_const)
results=myModel.fit()
print(results.summary())OLS Regression Results ============================================================================== Dep. Variable: y R-squared: 0.897 Model: OLS Adj. R-squared: 0.896 Method: Least Squares F-statistic: 570.3 Date: Thu, 09 Nov 2023 Prob (F-statistic): 1.58e-96 Time: 20:01:27 Log-Likelihood: -386.18 No. Observations: 200 AIC: 780.4 Df Residuals: 196 BIC: 793.6 Df Model: 3 Covariance Type: nonrobust ============================================================================== coef std err t P>|t| [0.025 0.975] ------------------------------------------------------------------------------ const 2.9389 0.312 9.422 0.000 2.324 3.554 x1 0.0458 0.001 32.809 0.000 0.043 0.049 x2 0.1885 0.009 21.893 0.000 0.172 0.206 x3 -0.0010 0.006 -0.177 0.860 -0.013 0.011 ============================================================================== Omnibus: 60.414 Durbin-Watson: 2.084 Prob(Omnibus): 0.000 Jarque-Bera (JB): 151.241 Skew: -1.327 Prob(JB): 1.44e-33 Kurtosis: 6.332 Cond. No. 454. ============================================================================== Notes: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
重点考虑参数R-squared、Prob(F-statistic)以及P>|t|的两个值,通过这4个参数就能判断模型是否线性显著,同时知道显性的程度。
其中,R-squared(决定系数)=SSR/SST,取值范围为[0,1],其值越接近1,说明回归效果越好。在这里,R-squared的值为0.897,接近于1,说明回归效果好。F-statistic(F检验)的值越大越能推翻原假设,原假设是“我们的模型不是线性模型”。Prob(F-statistic)是F-statistic的概率,这个值越小越能拒绝原假设,这里为1.58e-96,该值非常小,足以证明是线性显著的。
接着,采用机器学习的方法再进行建模,以便进行两者的对比分析。为了采用机器学习方法,需要拆分训练集和测试机。在这里通过调用sklearn.model_selection中的train_test_split()方法进行训练姐和测试集的拆分,random_state为1,采用25%的数据测试,75%的数据训练。
#第二种分析方法——基于机器学习
#拆分训练集和测试集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(Data,sales,random_state=1,test_size=0.25)查看训练数据和测试数据的数量:
#查看训练数据和测试数据的数量
print(X_train.shape)
print(X_test.shape)(150, 3) (50, 3)
在训练集上训练模型。这里调用sklearn.linear_model中默认参数的LinearRegression对训练集进行线性回归。
from sklearn.linear_model import LinearRegression
linreg=LinearRegression()
model=linreg.fit(X_train,y_train)
print(model)LinearRegression()
在此基础上,查看多元线性回归模型的回归系数:
model.coef_array([0.04656457, 0.17915812, 0.00345046])
查看回归模型的截距:
model.intercept_2.8769666223179335
最后,调用score()方法返回预测的R-squared(决定系数),即模型的准确率:
#准确率
model.score(X_test,y_test)0.9156213613792232
八、模型预测
采用predict()方法使用线性模型进行预测,返回模型的预测结果y_pred:
y_pred=linreg.predict(X_test)
y_predarray([21.70910292, 16.41055243, 7.60955058, 17.80769552, 18.6146359 , 23.83573998, 16.32488681, 13.43225536, 9.17173403, 17.333853 , 14.44479482, 9.83511973, 17.18797614, 16.73086831, 15.05529391, 15.61434433, 12.42541574, 17.17716376, 11.08827566, 18.00537501, 9.28438889, 12.98458458, 8.79950614, 10.42382499, 11.3846456 , 14.98082512, 9.78853268, 19.39643187, 18.18099936, 17.12807566, 21.54670213, 14.69809481, 16.24641438, 12.32114579, 19.92422501, 15.32498602, 13.88726522, 10.03162255, 20.93105915, 7.44936831, 3.64695761, 7.22020178, 5.9962782 , 18.43381853, 8.39408045, 14.08371047, 15.02195699, 20.35836418, 20.57036347, 19.60636679])
九、模型评价
对预测结果评价,这里采用matplotlib.pyplot的plot()函数绘制预测结果与真实值图,两条线分别表示模型预测值和观察值。
import matplotlib.pyplot as plt
plt.figure()
plt.plot(range(len(y_pred)),y_pred,'b',label="predict")
plt.plot(range(len(y_pred)),y_test,'r',label="test")
plt.legend(loc="upper right")
plt.xlabel("the number of sales")
plt.ylabel("value of sales")
plt.show()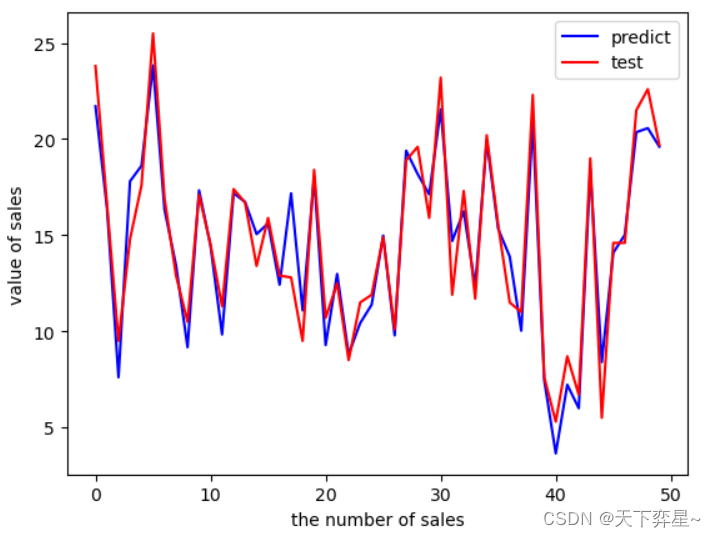
从运行结果可以看出,预测结果与真实值的折线趋于重合,此结果说明模型的预测结果较好。