文章目录
- 平面上点到直线的距离
- 点到平面的距离
- 小结
- 角平分面问题
- 例
- 点到直线的距离
平面上点到直线的距离
- 设坐标平面上有点 P ( x 1 , y 1 ) P(x_1,y_1) P(x1,y1)和直线 l : A x + B y + C = 0 l:Ax+By+C=0 l:Ax+By+C=0, A , B A,B A,B不全为0
- 点
P
P
P到直线
l
l
l的的距离的算法推导如下
- 作直线 m m m通过点 P ( x 1 , y 1 ) P(x_1,y_1) P(x1,y1),并且和直线 l l l垂直,设垂足为 P 0 ( x 0 , y 0 ) P_0(x_0,y_0) P0(x0,y0)
- 令:
d
2
=
∣
P
0
P
1
∣
2
=
(
x
1
−
x
0
)
2
+
(
y
1
−
y
0
)
2
d^2=|P_0P_1|^2=(x_1-x_0)^2+(y_1-y_0)^2
d2=∣P0P1∣2=(x1−x0)2+(y1−y0)2
(0),所求的就是 d d d - 由直线垂直对应的方程关系可设直线
P
P
0
PP_0
PP0的方程为
B
x
−
A
y
+
D
=
0
B{x}-Ay+D=0
Bx−Ay+D=0
(1)- 因为
P
P
P在
P
P
0
PP_0
PP0上,从而
B
x
0
−
A
y
0
+
D
=
0
Bx_0-Ay_0+D=0
Bx0−Ay0+D=0
(1-1) - 两式相减,得
B
(
x
−
x
0
)
−
A
(
y
−
y
0
)
=
0
B(x-x_0)-A(y-y_0)=0
B(x−x0)−A(y−y0)=0
(1-2) - 将
P
0
P_0
P0代入到(1-2),得
B
(
x
0
−
x
1
)
−
A
(
y
0
−
y
1
)
B(x_0-x_1)-A(y_0-y_1)
B(x0−x1)−A(y0−y1)=0
(1-3)
- 因为
P
P
P在
P
P
0
PP_0
PP0上,从而
B
x
0
−
A
y
0
+
D
=
0
Bx_0-Ay_0+D=0
Bx0−Ay0+D=0
- 又因为
P
0
P_0
P0还在
l
l
l上,从而
A
x
0
+
B
y
0
+
C
=
0
Ax_0+By_0+C=0
Ax0+By0+C=0,从而
C
=
−
A
x
0
−
B
y
0
C=-Ax_0-By_0
C=−Ax0−By0
(1-4), - 构造
t
=
A
x
1
+
B
y
1
+
C
t=Ax_1+By_1+C
t=Ax1+By1+C,由(1-4),得
t
=
A
x
1
+
B
y
1
−
A
x
0
−
B
y
0
t=Ax_1+By_1-Ax_0-By_0
t=Ax1+By1−Ax0−By0=
A
(
x
1
−
x
0
)
+
B
(
y
1
−
y
0
)
A(x_1-x_0)+B(y_1-y_0)
A(x1−x0)+B(y1−y0)
(1-5),即 A ( x 1 − x 0 ) + B ( y 1 − y 0 ) = t A(x_1-x_0)+B(y_1-y_0)=t A(x1−x0)+B(y1−y0)=t(1-6)- 将(1-3)两边平方加上(1-6)两边平方,整理得
-
(
A
2
+
B
2
)
[
(
x
1
−
x
0
)
2
+
(
y
−
y
0
)
2
]
(A^2+B^2)[(x_1-x_0)^2+(y-y_0)^2]
(A2+B2)[(x1−x0)2+(y−y0)2]=
t
2
t^2
t2
(1-7);代入(0),得 ( A 2 + B 2 ) d 2 (A^2+B^2)d^2 (A2+B2)d2= t 2 t^2 t2 - 所以 d 2 d^2 d2= t 2 ( A 2 + B 2 ) \frac{t^2}{(A^2+B^2)} (A2+B2)t2
-
d
d
d=
∣
t
∣
A
2
+
B
2
\frac{|t|}{\sqrt{A^2+B^2}}
A2+B2∣t∣=
∣
A
x
1
+
B
y
1
+
C
∣
A
2
+
B
2
\frac{|Ax_1+By_1+C|}{\sqrt{A^2+B^2}}
A2+B2∣Ax1+By1+C∣
(1-8)
文章目录
- 平面上点到直线的距离
- 点到平面的距离
- 小结
- 角平分面问题
- 例
- 点到直线的距离
点到平面的距离
-
-
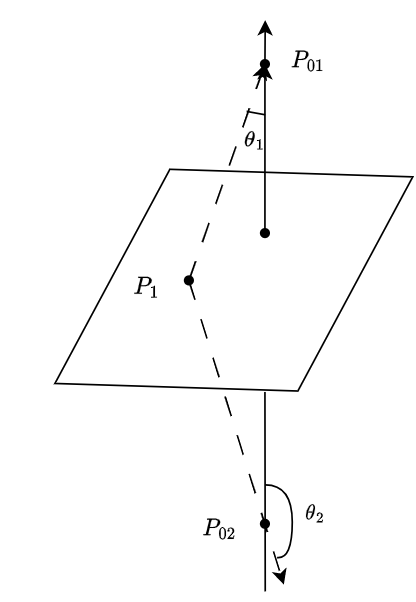
设 P 0 ( x 0 , y 0 , z 0 ) P_0(x_0,y_0,z_0) P0(x0,y0,z0)是平面 Π : A x + B y + C z + D = 0 \Pi:Ax+By+Cz+D=0 Π:Ax+By+Cz+D=0
(1)外一点,求 P 0 P_0 P0到 Π \Pi Π的距离 d d d-
设平面的法向量为 n = ( A , B , C ) \boldsymbol{n}=(A,B,C) n=(A,B,C)
(1-1),其朝向记为 d 1 \boldsymbol{d_1} d1, − n -\boldsymbol{n} −n也是 Π \Pi Π的法向量,其朝向记为 d 2 \boldsymbol{d_2} d2 -
我们只需要讨论其中的一种情况,另一种情况由于条件的对称性,同理,具有相同的结论
-
-
下面讨论点 P 0 P_0 P0分别位于 d 1 , d 2 \boldsymbol{d_1,d_2} d1,d2侧时的情形
- 将位于 d 1 \boldsymbol{d_1} d1侧时的 P 0 P_0 P0,记为 P 01 P_{01} P01,位于 d 2 \boldsymbol{d_2} d2侧时记为 P 02 P_{02} P02
-
分析可知,法向量 n \boldsymbol{n} n和 P 1 P 01 → \overrightarrow{P_{1}P_{01}} P1P01的夹角 θ 1 ∈ ( 0 , π 2 ) \theta_1\in(0,\frac{\pi}{2}) θ1∈(0,2π), n \boldsymbol{n} n和 P 1 P 02 → \overrightarrow{P_1P_{02}} P1P02的夹角为 θ 2 ∈ ( π 2 , π ) \theta_{2}\in(\frac{\pi}{2},\pi) θ2∈(2π,π)
- 距离分别记为
h
1
=
∣
P
1
P
01
→
∣
cos
θ
1
h_1=|\overrightarrow{P_{1}P_{01}}|\cos{\theta_1}
h1=∣P1P01∣cosθ1
(2)和 h 2 = ∣ P 1 P 02 → ∣ cos ( π − θ 2 ) = ∣ P 1 P 02 → ∣ ( − cos θ 2 ) h_2=|\overrightarrow{P_{1}P_{02}}|\cos{(\pi-\theta_2)}=|\overrightarrow{P_{1}P_{02}}|(-\cos{\theta_2)} h2=∣P1P02∣cos(π−θ2)=∣P1P02∣(−cosθ2)(3)-
其中 cos θ 2 < 0 \cos\theta_{2}<0 cosθ2<0,即 − cos θ 2 > 0 -\cos\theta_{2}>0 −cosθ2>0,从而 h 2 = ∣ P 1 P 02 → ∣ ∣ cos θ 2 ∣ h_2=|\overrightarrow{P_{1}P_{02}}||\cos{\theta_2|} h2=∣P1P02∣∣cosθ2∣
(4) -
另一方面, cos θ 1 > 0 \cos\theta_1>0 cosθ1>0,即 ∣ cos θ 1 ∣ = cos θ 1 |\cos\theta_1|=\cos\theta_1 ∣cosθ1∣=cosθ1,从而 h 1 = ∣ P 1 P 01 → ∣ cos θ 1 h_1=|\overrightarrow{P_{1}P_{01}}|\cos{\theta_1} h1=∣P1P01∣cosθ1= ∣ P 1 P 01 → ∣ ∣ cos θ 1 ∣ |\overrightarrow{P_{1}P_{01}}||\cos{\theta_1}| ∣P1P01∣∣cosθ1∣
(5)
-
- 距离分别记为
h
1
=
∣
P
1
P
01
→
∣
cos
θ
1
h_1=|\overrightarrow{P_{1}P_{01}}|\cos{\theta_1}
h1=∣P1P01∣cosθ1
-
从而 h 1 , h 2 h_1,h_2 h1,h2的计算公式形式一致,因此点 P 0 P_0 P0到 Π \Pi Π的距离公式为: h = ∣ P 1 P 0 → ∣ ∣ cos θ ∣ h=|\overrightarrow{P_{1}P_{0}}||\cos{\theta}| h=∣P1P0∣∣cosθ∣
(6)
小结
-
P 1 P 0 → = ( x 0 − x 1 , y 0 − y 1 , z 0 − z 1 ) \overrightarrow{P_1P_0}=(x_0-x_1,y_0-y_1,z_0-z_1) P1P0=(x0−x1,y0−y1,z0−z1)
(7) -
h h h= ∣ P 1 P 0 → ∣ ∣ cos θ ∣ |\overrightarrow{P_1P_0}||\cos\theta| ∣P1P0∣∣cosθ∣= ∣ P 1 P 0 → ∣ ∣ P 1 P 0 → ⋅ n ∣ ∣ P 1 P 0 → ∣ ∣ n ∣ |\overrightarrow{P_1P_0}| \frac{|\overrightarrow{P_1P_0}\cdot{\boldsymbol{n}}|}{|\overrightarrow{P_1P_0}||\boldsymbol{n|}} ∣P1P0∣∣P1P0∣∣n∣∣P1P0⋅n∣= ∣ P 1 P 0 → ⋅ n ∣ ∣ n ∣ \frac{|\overrightarrow{P_1P_0}\cdot{\boldsymbol{n}}|}{|\boldsymbol{n}|} ∣n∣∣P1P0⋅n∣
(8) -
将(1-1),(7)带入(8):得式
(9)- h = ∣ ( x 0 − x 1 , y 0 − y 1 , z 0 − z 1 ) ⋅ ( A , B , C ) ∣ A 2 + B 2 + C 2 = ∣ A ( x 0 − x 1 ) + B ( y 0 − y 1 ) + C ( z 0 − z 1 ) ∣ A 2 + B 2 + C 2 = ∣ A x 0 − A x 1 + B y 0 − B y 1 + C z 0 − C z 1 ∣ A 2 + B 2 + C 2 = ∣ A x 0 + B y 0 + C z 0 − ( A x 1 + B y 1 + C z 1 ) ∣ A 2 + B 2 + C 2 h=\frac{|(x_0-x_1,y_0-y_1,z_0-z_1)\cdot(A,B,C)|} {\sqrt{A^2+B^2+C^2}} \\ =\frac{|A(x_0-x_1)+B(y_0-y_1)+C(z_0-z_1)|} {\sqrt{A^2+B^2+C^2}} \\ =\frac{|Ax_0-Ax_1+By_0-By_1+Cz_0-Cz_1|} {\sqrt{A^2+B^2+C^2}} \\ =\frac{|Ax_0+By_0+Cz_0-(Ax_1+By_1+Cz_1)|} {\sqrt{A^2+B^2+C^2}} h=A2+B2+C2∣(x0−x1,y0−y1,z0−z1)⋅(A,B,C)∣=A2+B2+C2∣A(x0−x1)+B(y0−y1)+C(z0−z1)∣=A2+B2+C2∣Ax0−Ax1+By0−By1+Cz0−Cz1∣=A2+B2+C2∣Ax0+By0+Cz0−(Ax1+By1+Cz1)∣
-
由于 P 1 ∈ Π P_1\in\Pi P1∈Π,所以 A x 1 + B y 1 + C z 1 + D = 0 Ax_1+By_1+Cz_1+D=0 Ax1+By1+Cz1+D=0
(10),即 − ( A x 1 + B y 1 + C z ) = D -(Ax_1+By_1+C_z)=D −(Ax1+By1+Cz)=D(10-1) -
所以有
(11)- h = ∣ A x 0 + B y 0 + C z 0 + D ∣ A 2 + B 2 + C 2 h=\frac{|Ax_0+By_0+Cz_0+D|} {\sqrt{A^2+B^2+C^2}} h=A2+B2+C2∣Ax0+By0+Cz0+D∣
角平分面问题
- 平面 Π 1 , Π 2 \Pi_1,\Pi_2 Π1,Π2的角平分上的点到两平面的距离相等(点线距问题),来建立方程
例
-
点 P ( 2 , 1 , 1 ) P(2,1,1) P(2,1,1)到 Π : x + y − z + 1 = 0 \Pi:x+y-z+1=0 Π:x+y−z+1=0的距离:
- h = ∣ 2 + 1 − 1 + 1 ∣ 1 + 1 + 1 = 3 h=\frac{|2+1-1+1|}{\sqrt{1+1+1}}=\sqrt{3} h=1+1+1∣2+1−1+1∣=3
点到直线的距离
- 设 M 0 ( x 0 , y 0 , z 0 ) M_0(x_0,y_0,z_0) M0(x0,y0,z0)是直线外的一点
-
M
(
x
,
y
,
z
)
M(x,y,z)
M(x,y,z)是直线
l
l
l:
x
−
x
1
m
=
y
−
y
1
n
=
z
−
z
1
p
\frac{x-x_1}{m}=\frac{y-y_1}{n}=\frac{z-z_1}{p}
mx−x1=ny−y1=pz−z1上的一点,求点
M
0
M_0
M0到直线
l
l
l的距离
d
d
d
- 直线的方向向量为
s
=
(
m
,
n
,
p
)
\bold{s}=(m,n,p)
s=(m,n,p)
(1),因此可以在直线 l l l上截取两点构造和 s \bold{s} s相等的向量 - 不妨取 M 1 ( x + m , y + n , z + p ) M_1(x+m,y+n,z+p) M1(x+m,y+n,z+p),则 M M 1 → \overrightarrow{MM_1} MM1= s \bold{s} s
- 又
M
0
M
→
\overrightarrow{M_0M}
M0M=
(
x
−
x
0
,
y
−
y
0
,
z
−
z
0
)
(x-x_0,y-y_0,z-z_0)
(x−x0,y−y0,z−z0)
(2),记为 m \bold{m} m= M 0 M → \overrightarrow{M_0M} M0M - 由向量积的几何意义可知, S = ∣ s × m ∣ S=|\bold{s\times{m}}| S=∣s×m∣为以 s , m \bold{s,m} s,m为邻边的平行四边形的面积
- 又
S
=
∣
M
M
1
∣
d
S=|MM_1|d
S=∣MM1∣d=
∣
s
∣
d
|\bold{s}|d
∣s∣d,所以
d
=
S
∣
s
∣
d=\frac{S}{|\bold{s}|}
d=∣s∣S=
∣
s
×
m
∣
∣
s
∣
\frac{|\bold{s\times{m}}|}{|\bold{s}|}
∣s∣∣s×m∣
(3),再找到直线 l l l上的一点,例如 ( x 1 , y 1 , z 1 ) (x_1,y_1,z_1) (x1,y1,z1)代入点 M M M,可以算出具体的 m \bold{m} m向量 ( x 1 − x 0 , y 1 − y 0 , z 1 − z 0 ) (x_1-x_0,y_1-y_0,z_1-z_0) (x1−x0,y1−y0,z1−z0)- ∣ s ∣ |\bold{s}| ∣s∣= m 2 + n 2 + p 2 \sqrt{m^2+n^2+p^2} m2+n2+p2
- ∣ s × m ∣ |\bold{s\times{m}}| ∣s×m∣= ∣ ( x 1 − x 0 , y 1 − y 0 , z 1 − z 0 ) × ( m , n , p ) ∣ |(x_1-x_0,y_1-y_0,z_1-z_0)\times{(m,n,p)}| ∣(x1−x0,y1−y0,z1−z0)×(m,n,p)∣
- 即 d d d= ∣ ( x 1 − x 0 , y 1 − y 0 , z 1 − z 0 ) × ( m , n , p ) ∣ m 2 + n 2 + p 2 \Large\frac{|(x_1-x_0,y_1-y_0,z_1-z_0)\times{(m,n,p)}|}{\sqrt{m^2+n^2+p^2}} m2+n2+p2∣(x1−x0,y1−y0,z1−z0)×(m,n,p)∣
- 直线的方向向量为
s
=
(
m
,
n
,
p
)
\bold{s}=(m,n,p)
s=(m,n,p)