这里写目录标题
- 代码解释
- 数组转化为列表,方便在哪里
- yeild
- range()函数还有一些常用的小技巧。在这里我们列举两个常用技巧,以供参考
- 梯度
- l.sum().backward()的粗浅理解
- detatch
- 文字描述
- 在默认情况下,PyTorch会累积梯度,我们需要清除之前的值 x.grad.zero_()
- detach作用
- tensor.detach_()不同于detach()
- 遍历而已return [text_labels[int(i)] for i in labels]
- 待解决
代码解释
class Timer: #@save
"""记录多次运行时间"""
def __init__(self):
self.times = []
self.start()
def start(self):
"""启动计时器"""
self.tik = time.time()
def stop(self):
"""停止计时器并将时间记录在列表中"""
self.times.append(time.time() - self.tik)
return self.times[-1]
def avg(self):
"""返回平均时间"""
return sum(self.times) / len(self.times)
def sum(self):
"""返回时间总和"""
return sum(self.times)
def cumsum(self):
"""返回累计时间"""
return np.array(self.times).cumsum().tolist()
def cumsum(self):
"""返回累计时间"""
return np.array(self.times).cumsum().tolist()
数组转化为列表,方便在哪里
yeild
def data_iter(batch_size, features, labels):
num_examples = len(features)
indices = list(range(num_examples))
# 这些样本是随机读取的,没有特定的顺序
random.shuffle(indices)
for i in range(0, num_examples, batch_size):
batch_indices = torch.tensor(
indices[i: min(i + batch_size, num_examples)])
yield features[batch_indices], labels[batch_indices]
range()函数还有一些常用的小技巧。在这里我们列举两个常用技巧,以供参考
1、生成指定步长的整数序列
通过给range()函数指定步长,可以生成指定步长的整数序列。例如,下面的代码将生成0到9之间的偶数序列。
for i in range(0, 10, 2):
print(i)
输出结果:
0
2
4
6
8
2、倒序遍历
通过指定开始与结束位置不同的参数,可以遍历一个倒序序列。例如,在一个列表中逆序遍历所有元素,可以使用以下方式:
arr = ['a', 'b', 'c', 'd', 'e']
for i in range(len(arr)-1, -1, -1):
print(arr[i])
输出结果为:
e
d
c
b
a
梯度
>>> x = torch.ones(2, 2, requires_grad=True) # 2x2全为1的tensor
>>> y = x + 2
>>> z = y * y * 3
>>> out = z.mean()
>>> print(z, out)
tensor([[27., 27.],
[27., 27.]], grad_fn=<MulBackward0>) tensor(27., grad_fn=<MeanBackward0>)
>>> out.backward()
>>> print(x.grad)
tensor([[4.5000, 4.5000],
[4.5000, 4.5000]])
grad_fn=
x.grad.zero_()
y = x.sum()
y
# y.backward()
# x.grad
tensor(6., grad_fn=)

l.sum().backward()的粗浅理解
梯度下降的优化方法,
参数发生改变导致的损失函数loss值变化多少,就是梯度


梯度下降就是 遵循着公式,在损失函数递减的方向上更新权重和偏置

对梯度的基础概念了解不到位叭,爆炸!
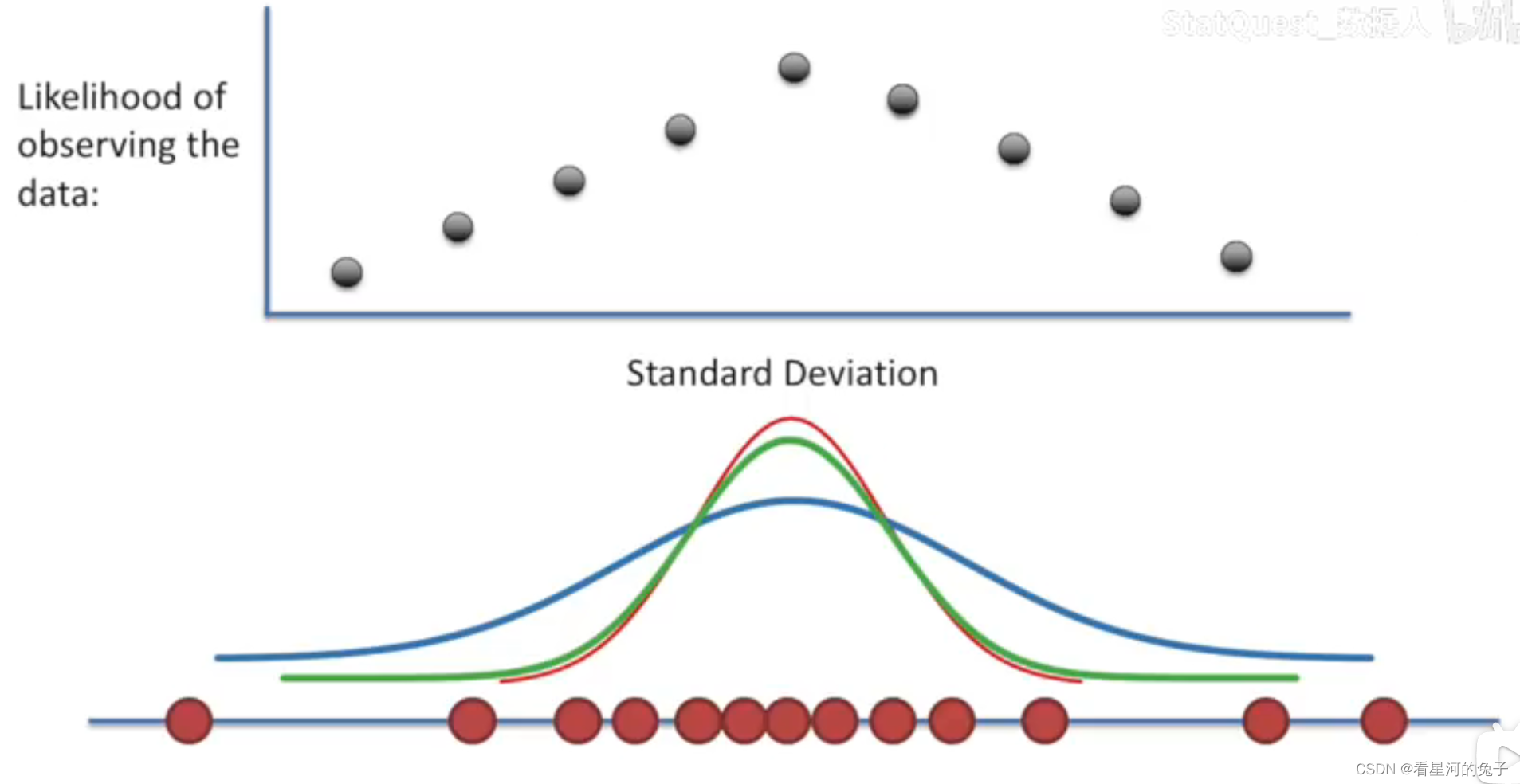
梯度是 ,loss值对x求导?不准确。比如给定一个batch的样本输入,在每个样本点上loss值对样本输入值求导 组成的 list。一组batch的输入对应的loss值是一个值,可是梯度确是这个loss值对不同的x求导的导数 作为元素,组成 梯度
曾记否,滑滑梯的那张PPT,那个样本点的斜率,只是组成了梯度的一个元素而已
输入样本x是多个,对应的权重数组也是多个元素组成
那么梯度下降,粗略记忆是,loss值对w求导,这个没啥好说的
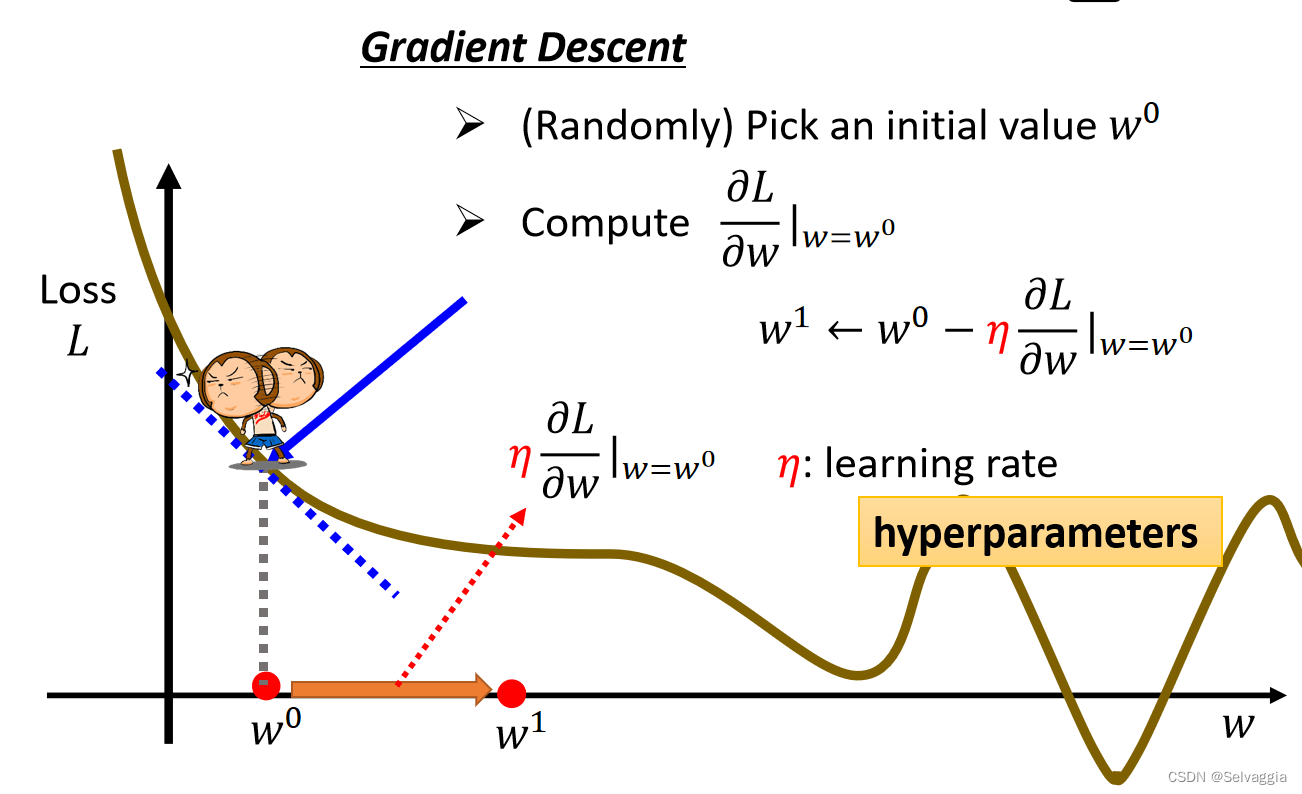
主要是,梯度 不是一个元素,是一个向量(但愿可以这样讲),是多维的
在损失函数递减的方向上更新权重和偏置,递减的方向 可不是某一个方向,而是对应的各个输入x的梯度方向
loss值是一个值,但是他是 多维的输入 通过多维的权重和偏置 sum在一起组成的
在代码里面求loss,得到的其实是个多维的向量,多维的输入(x1,x2,……) 操作得到的
# 训练
lr = 0.03
num_epochs = 3 # 迭代次数
batch_size = 10
net = linreg
loss = squred_loss
# 训练模型
for epoch in range(num_epochs):
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y) # 计算损失函数
l.sum().backward() # 计算各个参数的梯度
sgd([w, b], lr, batch_size) # 更新参数
detatch
import torch
def fun(x):
return x * x;
a = torch.tensor([1, 2, 3.], requires_grad=True)
print(a.grad)
out = fun(a)
out.sum().backward()
print(a.grad)
'''返回:
None
tensor([2., 4., 6.])
'''
import torch
def fun(x):
return x * x;
a = torch.tensor([1, 2, 3.], requires_grad=True)
print(a.grad) #None
out = fun(a)
print(out) # tensor([1., 4., 9.], grad_fn=<MulBackward0>)
# 添加detach(),c的requires_grad为False
c = out.detach()
print(c) # tensor([1., 4., 9.]),detatch之后断绝了c和a的关系,out和a是有关系的
# 这时候没有对c进行更改,所以并不会影响backward(),c更改也会影响out.sum().backward()
out.sum().backward()
print(a.grad) #tensor([2., 4., 6.])
# a.grad.zero_()
# c.sum().backward()
# print(a.grad) 会报错,c是被detach出了关系树,无求得c对a的导数
'''返回:
None
tensor([0.7311, 0.8808, 0.9526], grad_fn=<SigmoidBackward>)
tensor([0.7311, 0.8808, 0.9526])
tensor([0.1966, 0.1050, 0.0452])
'''
文字描述
1、返回一个新的tensor,从当前计算图中分离下来。但是仍指向原变量的存放位置,不同之处只是requirse_grad为false.得到的这个tensir永远不需要计算器梯度,不具有grad.

从上可见tensor c是由out分离得到的,但是我也没有去改变这个c,这个时候依然对原来的out求导是不会有错误的,即
c,out之间的区别是c是没有梯度的,out是有梯度的
当使用detach()分离tensor,然后用这个分离出来的tensor去求导数,会影响backward(),会出现错误
2、使用detach返回的tensor和原始的tensor共同一个内存,即一个修改另一个也会跟着改变
当使用detach()分离tensor并且更改这个tensor时,即使再对原来的out求导数,会影响backward(),会出现错误
如果此时对c进行了更改,这个更改会被autograd追踪,在对out.sum()进行backward()时也会报错,因为此时的值进行backward()得到的梯度是错误的:
import torch
a = torch.tensor([1, 2, 3.], requires_grad=True)
print(a.grad)
out = a.sigmoid()
print(out)
#添加detach(),c的requires_grad为False
c = out.detach()
print(c)
c.zero_() #使用in place函数对其进行修改
#会发现c的修改同时会影响out的值
print(c)
print(out)
#这时候对c进行更改,所以会影响backward(),这时候就不能进行backward(),会报错
out.sum().backward()
print(a.grad)
'''返回:
None
tensor([0.7311, 0.8808, 0.9526], grad_fn=<SigmoidBackward>)
tensor([0.7311, 0.8808, 0.9526])
tensor([0., 0., 0.])
tensor([0., 0., 0.], grad_fn=<SigmoidBackward>)
Traceback (most recent call last):
File "test.py", line 16, in <module>
out.sum().backward()
File "/anaconda3/envs/deeplearning/lib/python3.6/site-packages/torch/tensor.py", line 102, in backward
torch.autograd.backward(self, gradient, retain_graph, create_graph)
File "/anaconda3/envs/deeplearning/lib/python3.6/site-packages/torch/autograd/__init__.py", line 90, in backward
allow_unreachable=True) # allow_unreachable flag
RuntimeError: one of the variables needed for gradient computation has been modified
by an inplace operation
'''
1、返回一个新的tensor,从当前计算图中分离下来的,但是仍指向原变量的存放位置,不同之处只是requires_grad为false,得到的这个tensor永远不需要计算其梯度,不具有grad
2、在新的计算中,不会再对其值的梯度进行修改
3、如果对返回张量进行backwark()计算,会出现错误
在默认情况下,PyTorch会累积梯度,我们需要清除之前的值 x.grad.zero_()
要清除就输入一次:x.grad.zero_()
detach作用
当我们再训练网络的时候可能希望保持一部分的网络参数不变,只对其中一部分的参数进行调整;或者值训练部分分支网络,并不让其梯度对主网络的梯度造成影响,这时候我们就需要使用detach()函数来切断一些分支的反向传播
假设有模型A和模型B,我们需要将A的输出作为B的输入,但训练时我们只训练模型B. 那么可以这样做:
input_B = output_A.detach()
它可以使两个计算图的梯度传递断开,从而实现我们所需的功能。
内容来源
tensor.detach_()不同于detach()
将一个tensor从创建它的图中分离,并把它设置成叶子tensor
其实就相当于变量之间的关系本来是x -> m -> y,这里的叶子tensor是x,但是这个时候对m进行了m.detach_()操作,其实就是进行了两个操作:
- 将m的grad_fn的值设置为None,这样m就不会再与前一个节点x关联,这里的关系就会变成x, m -> y,此时的m就变成了叶子结点
- 然后会将m的requires_grad设置为False,这样对y进行backward()时就不会求m的梯度
总结:其实detach()和detach_()很像,两个的区别就是detach_()是对本身的更改,detach()则是生成了一个新的tensor
比如x -> m -> y中如果对m进行detach(),后面如果反悔想还是对原来的计算图进行操作还是可以的
但是如果是进行了detach_(),那么原来的计算图也发生了变化,就不能反悔了
遍历而已return [text_labels[int(i)] for i in labels]
def get_fashion_mnist_labels(labels): #@save
"""返回Fashion-MNIST数据集的文本标签"""
text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
return [text_labels[int(i)] for i in labels]
get_fashion_mnist_labels((0,2,3))
# get_fashion_mnist_labels([1,2,3]) 都一样
['t-shirt', 'pullover', 'dress']
或者简单地理解
Y=XW+b
X和W都是多维的,b或许也是?或许不是
.sum()函数主要有两个作用,一个是用来求和,一个是用来降维。而在这里是用到了降维的作用。

X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
lr = 3e-2 # Learning rate
for i in range(10):
Y_hat = conv2d(X)
l = (Y_hat - Y) ** 2
conv2d.zero_grad()
l.sum().backward()
# Update the kernel
conv2d.weight.data[:] -= lr * conv2d.weight.grad
if (i + 1) % 2 == 0:
print(f'epoch {i + 1}, loss {l.sum():.3f}')
print(conv2d.weight.data.reshape((1, 2)))
待解决
Softmax回归的训练
def train_epoch_ch3(net, train_iter, loss, updater):
"""训练模型一个迭代周期(定义见第3章)。"""
if isinstance(net, torch.nn.Module): #如果是nn模具
net.train() #开启训练模式
metric = Accumulator(3) #长度为3的迭代器 来累积需要信息
for X, y in train_iter: #扫描数据
y_hat = net(X) #计算y_hat
l = loss(y_hat, y) #损失函数计算l
if isinstance(updater, torch.optim.Optimizer): #如果updater是pytorch的一个买者
updater.zero_grad() #梯度设为0
l.backward() #计算梯度
updater.step() #更新参数
metric.add( #样本数 累加数 正确的分类数 放到累加器里面
float(l) * len(y), accuracy(y_hat, y),
y.size().numel())
else: #如果从头开始实现
l.sum().backward() #l是一个向量 求和算梯度
updater(X.shape[0])
metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
return metric[0] / metric[2], metric[1] / metric[2]
#返回结果:损失/样本总数,所有分类正确的样本数/ 总样本数
训练函数
def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):
"""训练模型(定义见第3章)。"""
animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
legend=['train loss', 'train acc', 'test acc']) #可视化的animator(可忽略)
for epoch in range(num_epochs): #扫描n遍数据
train_metrics = train_epoch_ch3(net, train_iter, loss, updater) #训练一次
test_acc = evaluate_accuracy(net, test_iter) #在测试数据集上评估精度
animator.add(epoch + 1, train_metrics + (test_acc,)) #显示
train_loss, train_acc = train_metrics
assert train_loss < 0.5, train_loss
assert train_acc <= 1 and train_acc > 0.7, train_acc
assert test_acc <= 1 and test_acc > 0.7, test_acc