2023年辽宁省数学建模竞赛

B题 数据驱动的水下导航适配区分类预测

原题再现：

  “海洋强国”战略部署已成为推动中国现代化建设的重要组成部分，国家对此提出“发展海洋经济，保护海洋生态环境，加快建设海洋强国”的明确要求。
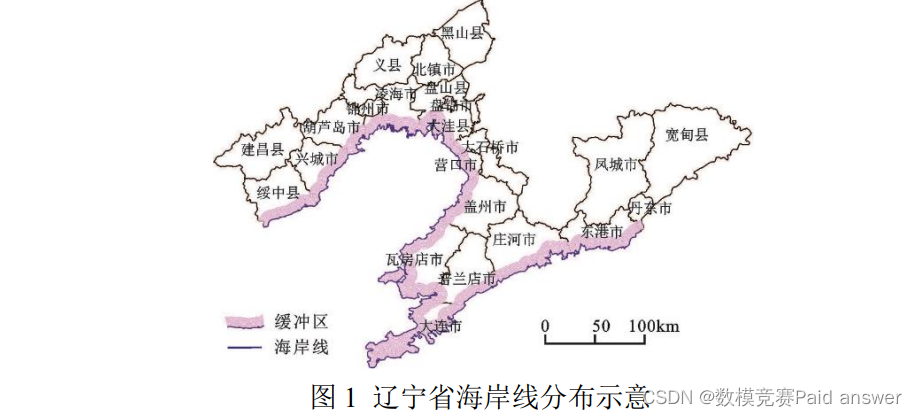
  《辽宁省“十四五”海洋经济发展规划》明确未来全省海洋经济的发展战略、发展目标、重大任务、空间部署和保障措施。规划范围包括辽宁省全部海域和大连、丹东、锦州、营口、盘锦和葫芦岛 6 个市以及海洋经济发展所依托的相关陆域，规划期限为 2021 年至 2025 年，展望到 2035 年。辽宁省作为中国最北沿海省份，拥有 2292.4 公里海岸线（如图 1 所示）。
  在“海洋强省”建设目标的背景下，完成海洋经济发展规划的目标重在海洋高新技术领域创新。其中关键核心技术之一是攻克水下导航与定位的适配区分类预测技术。

  水下航行器在执行水下任务时需要保持自主、无源、高隐蔽性、不受地域和时域限制、高精度的导航与定位。重力辅助导航是满足上述条件的主要方法之一。
  在重力辅助导航系统中，影响导航可靠性与精度的关键步骤是选择匹配性高的航行区域，即适配区。适配区的标定与识别技术是最具挑战性的问题之一。选取适配区前需要对研究海域的重力基准图（基础性的是重力异常基准图）进行插值加密处理，基于重力基准图所提供水下航行器航行区域的重力异常变化情况对适配区的选取进行分析。
  重力异常（值）的定义为：实际地球内部的物质密度分布不均匀，导致实际观测重力值与理论上的正常重力值总存在偏差，在排除各种干扰因素影响后，仅仅由地球物质密度分布不匀所引起的重力的变化，简称为重力异常。
  在重力异常变化显著区域，导航系统可获得高的定位精度；反之，在重力异常变化平坦区域，导航系统会出现定位精度的不敏感。由于不同区域的重力异常特征分布不同，建立可行的适配区分类预测模型，对保障水下航行器的导航精度至关重要。
  假设X为影响区域匹配性的特征属性指标，Y为刻画区域适配性的输出结果， F为以X为输入以Y为输出的分类预测系统。
  基于上述背景分析，请参考附件中的重力异常数据建立数学模型，解决以下问题：
  问题一：附件 1，给出一组分辨率为 1’×1’（相邻两格网点间的距离是 1’）的重力异常基准数据 A，试通过精细化基准图，合理划分区域，完成各区域的适配性标定（标签Y）。
  问题二：根据问题一中各划分区域的适配性标定结果Y ，合理选择区域的特征属性指标（特征X），试建立有效的区域适配区分类预测模型（系统F）。
  问题三：利用附件二中的重力异常基准数据 B，试对问题二所建立的系统F进行迁移性预测并讨论该系统F对新重力异常数据的适用性。
  附件
  附件 1：重力异常基准数据 A
  附件 2：重力异常基准数据 B

代码实例

from sklearn import datasets
#朴素贝叶斯

from sklearn.naive_bayes import GaussianNB
from sklearn.naive_bayes import MultinomialNB
from sklearn.naive_bayes import BernoulliNB
#SVM
from sklearn.svm import SVC
#KNN
from sklearn.neighbors import KNeighborsClassifier
#数据集分割
from sklearn.model_selection import train_test_split

cancers=datasets.load_breast_cancer()
X=cancers.data
Y=cancers.target
# 注意返回值： 训练集train，x_train，y_train，测试集test，x_test，y_test
# x_train为训练集的特征值，y_train为训练集的目标值，x_test为测试集的特征值，y_test为测试集的目标值
# 注意，接收参数的顺序固定
# 训练集占80%，测试集占20%
#此处是将数据集拆分为训练集和测试集
x_train,x_test,y_train,y_test=train_test_split(X, Y, test_size=0.2)
#朴素贝叶斯
#高斯贝叶斯分类器
model_linear =GaussianNB()
model_linear.fit(x_train, y_train)
train_score = model_linear.score(x_train, y_train)
test_score = model_linear.score(x_test, y_test)
print('高斯贝叶斯训练集的准确率:%.3f; 测试集的准确率:%.3f'%(train_score, test_score))
preresult=model_linear.predict(x_test)
print(preresult)
#多项式贝叶斯分类器
model_linear =MultinomialNB()
model_linear.fit(x_train, y_train)
train_score = model_linear.score(x_train, y_train)
test_score = model_linear.score(x_test, y_test)
print('多项式贝叶斯训练集的准确率:%.3f; 测试集的准确率:%.3f'%(train_score, test_score))
preresult=model_linear.predict(x_test)
print(preresult)
#伯努利贝叶斯分类器
model_linear=BernoulliNB()
model_linear.fit(x_train, y_train)
train_score = model_linear.score(x_train, y_train)
test_score = model_linear.score(x_test, y_test)
print('伯努利贝叶斯训练集的准确率:%.3f; 测试集的准确率:%.3f'%(train_score, test_score))
preresult=model_linear.predict(x_test)
print(preresult)
#SVM法

model_linear = SVC(C=1.0, kernel='linear')  # 线性核
model_linear.fit(x_train, y_train)
train_score = model_linear.score(x_train, y_train)
test_score = model_linear.score(x_test, y_test)
print('SVM法训练集的准确率:%.3f; 测试集的准确率:%.3f'%(train_score, test_score))
preresult=model_linear.predict(x_test)
print(preresult)
#KNN法
model_linear =KNeighborsClassifier(n_neighbors=15)
model_linear.fit(x_train, y_train)
train_score = model_linear.score(x_train, y_train)
test_score = model_linear.score(x_test, y_test)
print('KNN法训练集的准确率:%.3f; 测试集的准确率:%.3f'%(train_score, test_score))
preresult=model_linear.predict(x_test)
print(preresult)