参考文章
一、概念
用于描述顺序 & 区域,单使用无法产生效果。
图形绘制的本质是先画点再将点连接起来,所以点与点之间是存在一个先后顺序的。图形的方向影响的是:添加图形时确定闭合顺序(各个点的记录顺序)、图形的渲染结果(是判断图形渲染的重要条件)。
1.1 开放路径、闭合路径

1.2 判断点在图形内还是图形外
1.2.1 奇偶规则
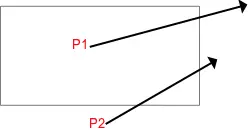
从任意位置 P 作一条射线,对与图形的边相交的点数进行判断:
- 若相交的点数为奇数,则认为 P 为图形内的点。
- 若相交的点数为偶数,则认为 P 为图形外的点。
1.2.2 非零环绕数规则
从任意位置 P 作一条射线,当 P 点沿射线方向移动时,对在每个方向上穿过射线的边进行判断:
- 每当图形的边从右到左穿过射线时 +1,从左到右穿过时 -1。
- 若环绕数为 ≠0 则 P 为图形内的点,否则为图形外的点。

二、创建对象
Path 的起点坐标默认为 (0,0)。
- 建全局 Path 对象,在 onDraw() 中按需修改,不要在 onDraw() 里创建,因为若 View 频繁刷新,就会频繁创建对象,拖慢刷新速度。
val path = Path()三、设置路径
| moveTo() | public void moveTo(float x, float y) 移动到新的坐标点,并作为新的起点,影响后续路径绘制。 |
| setLastPoint() | public void setLastPoint(float dx, float dy) 移动到新的坐标点,不会改变原有起点,不影响后续路径绘制。 |
| lineTo() | public void lineTo(float x, float y) 移动到新的坐标点,且和之前的点用直线连接。 |
| close() | public void close() 闭合路径,将当前点和起始点连接。如果终点和起点连接后仍无法形成封闭图形则什么也不做。 |
先 lineTo(400,500),分别使用 moveTo(300,300) 和 setLastPoint(300,300),再 lineTo(900,800),最后 close()。

四、重置路径
FillType 影响显示效果,数据结构影响重建速度,一般选择 reset()。
| reset() | public void reset() 保留 FillType 设置,不保留原有数据结构。 |
| rewind() | public void rewind() 不保留 FillType 设置,保留原有数据结构。 |
五、添加路径
5.1 基本图形
添加图形路径后会改变路径的起点。形参 dir 即方向 direction,指定绘制时是顺时针还是逆时针(CW为顺时针clockwise,CCW为逆时针counter-clockwise)。
| addRect() 矩形 | addRect(RectF rect, Path.Direction dir) 路径起点变为矩形的左上角顶点。 |
| addRoundRect() 圆角矩形 | addRoundRect(RectF rect, float rx, float ry, Path.Direction dir) |
| addArc() arcTo() 圆弧 | public void addArc (RectF oval, float startAngle, float sweepAngle) startAngle起始角度,sweepAngle绘制扫过的角度。 |
| public void arcTo (RectF oval, float startAngle, float sweepAngle) 与上面方法唯一不同的是:如果圆弧的起点和最后一个坐标点不相同,就连接两个点。 | |
| public void arcTo (RectF oval, float startAngle, float sweepAngle, boolean forceMoveTo) forceMoveTo:是否将之前路径的结束点设置为圆弧起点。设为 true 在新的起点画圆弧,不连接最后一个点与圆弧起点,即与之前路径没有交集(同第一个)。设为 false 在新的起点画圆弧,但会连接之前路径的结束点与圆弧起点,即与之前路径有交集(同第二个)。 | |
| addCircle() 圆形 | addCircle(float x, float y, float radius, Path.Direction dir) 路径起点变为圆在X轴正方向最大的点 。 |
| addOval() 椭圆形 | addOval(RectF oval, Path.Direction dir) oval作为椭圆的外切矩形区域。 |
canvas.translate(350, 500) //为了方便观察,平移坐标系
path.addRect(0, 0, 400, 400, Path.Direction.CW) //顺时针
//path.addRect(0,0,400,400, Path.Direction.CCW) //逆时针
canvas.drawPath(path paint)
5.1.1 矩形 addRect()
| addRect(RectF rect, Path.Direction dir) 路径起点变为矩形的左上角顶点。 |
5.1.2 圆角矩形 addRoundRect()
| addRoundRect(RectF rect, float rx, float ry, Path.Direction dir) |
5.1.3 圆弧 addArc()、arcTo()
| public void addArc (RectF oval, float startAngle, float sweepAngle) startAngle起始角度,sweepAngle绘制扫过的角度。 |
| public void arcTo (RectF oval, float startAngle, float sweepAngle) 与上面方法唯一不同的是:如果圆弧的起点和最后一个坐标点不相同,就连接两个点。 |
| public void arcTo (RectF oval, float startAngle, float sweepAngle, boolean forceMoveTo) forceMoveTo:是否将之前路径的结束点设置为圆弧起点。设为 true 在新的起点画圆弧,不连接最后一个点与圆弧起点,即与之前路径没有交集(同第一个)。设为 false 在新的起点画圆弧,但会连接之前路径的结束点与圆弧起点,即与之前路径有交集(同第二个)。 |
5.1.4 圆形 addCircle()
| addCircle(float x, float y, float radius, Path.Direction dir) 路径起点变为圆在X轴正方向最大的点 。 |
5.1.5 椭圆形 addOval()
| addOval(RectF oval, Path.Direction dir) oval作为椭圆的外切矩形区域。 |
5.2 合并路径 addPath()
| public void addPath(Path src) 将 src 路径添加过来,dx dy 是先偏移后再添加,matrix 是先变换后再添加。 |
canvas.translate(350, 500) //为了方便观察,平移坐标系
Path pathRect = new Path()
Path pathCircle = new Path()
pathRect.addRect(-200, -200, 200, 200, Path.Direction.CW) // 画一个矩形路径
pathCircle.addCircle(0, 0, 100, Path.Direction.CW) // 画一个圆形路径
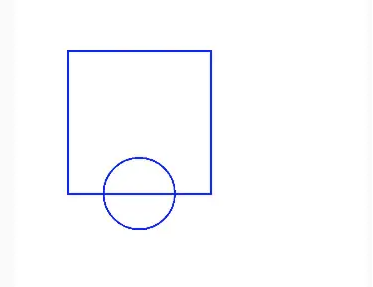
pathRect.addPath(pathCircle, 0, 200) // 将圆形路径移动(0,200),再添加到矩形路径里
canvas.drawPath(pathRect,mPaint1) // 绘制合并后的路径六、判断路径属性
6.1 内容是否为空 isEmpty()
| public boolean isEmpty() 判断path中是否包含内容。 |
6.2 是否为矩形 isRect()
| public boolean isRect(RectF rect) 判断path是否是一个矩形,如果是的话会将矩形信息方巾参数 rect 中。 |
path.lineTo(0,400)
path.lineTo(400,400)
path.lineTo(400,0)
path.lineTo(0,0)
RectF rect = new RectF()
boolean b = path.isRect(rect) //true
//rect存放信息:
//rect.left = 0
//rect.top = 0
//rect.right = 400
//rect.bottom = 4006.3 替换 set()
| public void set(Path src) 用 src 路径替代现有路径。 |
path1.addRect(-200,-200,200,200, Path.Direction.CW) //矩形路径
path2.addCircle(0,0,100, Path.Direction.CW) //圆形路径
path1.set(path2) //将圆形路径代替矩形路径6.4 偏移 offset()
| public void offset(float dx, float dy) public void offset(float dx, float dy, Path dst) 偏移位置,dst 用来存储平移后的路径状态但不影响当前路径。 |

canvas.translate(350, 500) //为了方便观察,平移坐标系
//path中添加一个圆形(圆心在坐标原点)
path = new Path()
path.addCircle(0, 0, 100, Path.Direction.CW)
//平移路径并存储平移后的状态
Path dst = new Path()
path.offset(400, 0, dst) //平移
canvas.drawPath(path, mPaint1) //绘制path
//通过dst绘制平移后的图形(红色)
mPaint1.setColor(Color.RED)
canvas.drawPath(dst,mPaint1)七、设置路径填充颜色 xxxFillType()

| getFillType() | public FillType getFillType() 设置填充规则。 |
| setFillType() | public void setFillType(FillType ft) 获取当前填充规则。 |
| isInverseFillType() | public boolean isInverseFillType() 判断是否是反向(INVERSE)规则。 |
| toggleInverseFillType() | public void toggleInverseFillType() 切换填充规则(即原有规则与反向规则之间相互切换)。 |
- 奇偶规则:EVEN_ODD
- 反奇偶规则:INVERSE_EVEN_ODD
- 非零环绕数规则:WINDING
- 反非零环绕数规则:INVERSE_WINDING

canvas.translate(350, 500) //为了方便观察,平移坐标系
path.addRect(-200, -200, 200, 200, Path.Direction.CW) // 在Path中添加一个矩形
path.setFillType(Path.FillType.EVEN_ODD) //设置Path填充模式为 奇偶规则
// path.setFillType(Path.FillType.INVERSE_EVEN_ODD) // 反奇偶规则
canvas.drawPath(path, mPaint1) //画出路径
八、布尔操作 op()

两个 Path 之间的运算,用简单的图形通过特定规则合成相对复杂的图形。
| public boolean op(Path path, Op op) 对调用的 path 和传入的 path 执行布尔运算,运算结果存入到调用该方法的 path 中。 |
| public boolean op(Path path1, Path path2, Op op) 对 path1 和 path2 执行布尔运算,运算结果存入到调用该方法的 path 中。 |

canvas.translate(550, 550) //为了方便观察,平移坐标系
//画两个圆
path1.addCircle(0, 0, 100, Path.Direction.CW)
path2.addCircle(50, 0,100, Path.Direction.CW)
//取两个路径的异或集
path1.op(path2, Path.Op.XOR)
//画出路径
canvas.drawPath(path1, mPaint1)
九、贝塞尔曲线
参考文章
计算曲线的数学公式,任何一条曲线都可以用贝塞尔曲线表示。
| 数据点 | 指路径的起始点和终止点。 |
| 控制点 | 决定了路径的弯曲轨迹。根据控制点的个数,贝塞尔曲线被分为一阶贝塞尔曲线(0个控制点)、二阶贝塞尔曲线(1个控制点)、三阶贝塞尔曲线(2个控制点)等等。n+1阶贝塞尔曲线 = 有n个控制点。(1阶 = 一条直线,高阶可以拆解为多条低阶曲线) |
| 绘制二阶贝赛尔曲线 | public void quadTo(float x1, float y1, float x2, float y2) (x1,y1)为控制点,(x2,y2)为终点 |
| public void rQuadTo(float dx1, float dy1, float dx2, float dy2) (x1,y1)为控制点距离起点的偏移量,(x2,y2)为终点距离起点的偏移量 | |
| 绘制三阶贝赛尔曲线 | public void conicTo(float x1, float y1, float x2, float y2, float weight) (x1,y1),(x2,y2)为控制点,(x3,y3)为终点 |
| public void rConicTo(float dx1, float dy1, float dx2, float dy2, float weight) (x1,y1),(x2,y2)为控制点距离起点的偏移量,(x3,y3)为终点距离起点的偏移量 |