线性系统的激励和响应以及与系统特性的联系
一、系统激励和响应的定义
一个线性系统可以用一个常系数线性微分方程来表示。比如,RC串联电路,电容器两端的电压
u
c
(
t
)
u_c(t)
uc(t)所满足的关系式为:
R
C
d
u
c
d
t
+
u
c
=
e
(
t
)
RC\frac{{d{u_c}}}{{dt}} + {u_c} = e(t)
RCdtduc+uc=e(t)
这是一个一阶常系数线性微分方程。
通常将外加电动势
e
(
t
)
e(t)
e(t)看成是这个系统(本例中,系统为RC电路)的随时间
t
t
t变化的输入函数,称为激励。同时将电容器两端的电压
u
c
(
t
)
u_c(t)
uc(t)看作是这个系统的随时间
t
t
t变化的输出函数,称为激励。
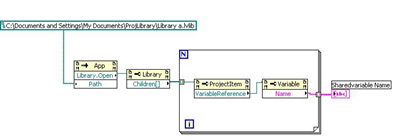
这样的 R C RC RC串联的闭合回路,就可以看成是一个有输入端和输出端的线性系统。如图1所示。
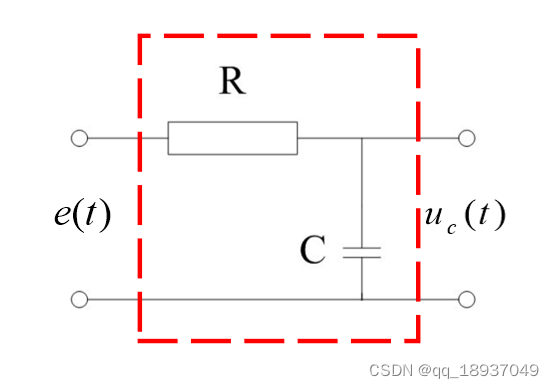
图1RC电路构成的线性系统
在图1中红色虚线框中的电路结构由系统内的元件参量和连接方式决定。
RC电路构成的线性系统,在电路理论中又称为线性网络(简称网络)。
二、激励、响应以及系统特性之间的联系
根据上面的例子可知:一个系统的响应是由激励函数与系统本身的特征(包括元件的参量和连接方式)所决定。对于不同的线性系统,即使在同一激励下,其响应也是不同的。
在分析线性系统时,有时并不关心系统内部的各种不同的结构情况,而是想研究激励和响应以及系统本身特性之间的联系,其响应也是不同的。
用图2表示激励、响应以及系统特性之间的联系。
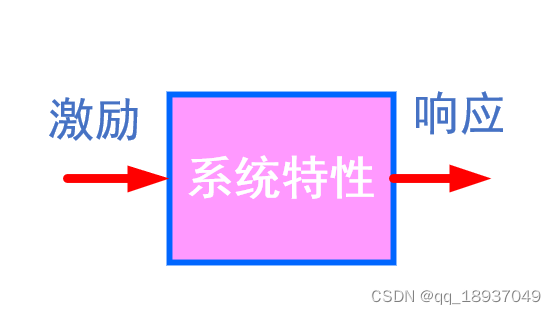
图2 激励、响应以及系统特性之间的联系
为了深入研究激励、响应与系统特性的联系,通常需要采用传递函数来研究。