题目
给你一个数组 points ,其中 points[i] = [ x i x_i xi, y i y_i yi] 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。
示例 1:
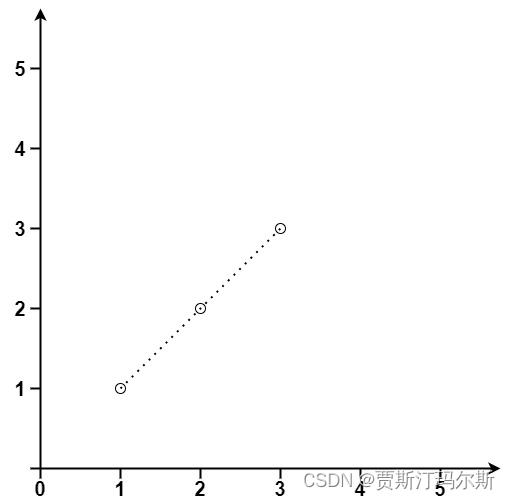
输入:points = [[1,1],[2,2],[3,3]]
输出:3
示例 2:
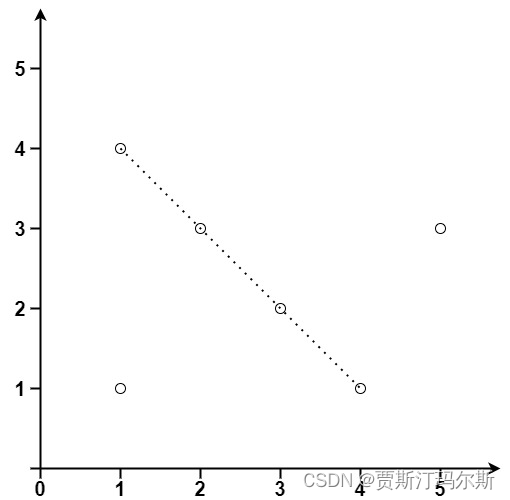
输入:points = [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
输出:4
提示:
1 <= points.length <= 300
points[i].length == 2
-104 <= xi, yi <= 1 0 4 10^4 104
points 中的所有点 互不相同
解
解决这个问题的常用方法是使用哈希表。对于给定的点 ( x i x_i xi, y i y_i yi),我们可以计算其与其他点的斜率 ( x j x_j xj - x i x_i xi) / ( y j y_j yj - y i y_i yi),并将这个斜率存储在哈希表中。
具体步骤如下:
- 遍历每一个点 ( x i x_i xi, y i y_i yi),对于每个点,初始化一个哈希表 slopeMap,用于存储以该点为起点的直线上的点数。
- 然后再次遍历每一个点 ( x j x_j xj, y j y_j yj)(这个循环将计算所有点与点 ( x i x_i xi, y i y_i yi) 的斜率),如果 ( x j x_j xj, y j y_j yj) 与 ( x i x_i xi, y i y_i yi) 重合,将 overlap 值加 1,否则计算斜率 ( x j x_j xj - x i x_i xi) / ( y j y_j yj - y i y_i yi)。
- 将计算得到的斜率存储在 slopeMap 中,如果已存在该斜率,直线上的点数加 1,如果不存在,则初始化为 2(包括 ( x i x_i xi, y i y_i yi) 和 ( x j x_j xj, y j y_j yj))。
- 在每次内循环结束后,更新 maxPoints,确保始终保持记录最多点的直线上的点数。
- 继续遍历下一个点 ( x i x_i xi, y i y_i yi),并重复上述过程,直到所有点都被处理。
以下是Java代码示例:
class Solution {
public int maxPoints(int[][] points) {
if (points.length < 3) {
return points.length;
}
int maxPoints = 2; // 初始化最大点数为2,因为至少有两个点在同一直线上
for (int i = 0; i < points.length; i++) {
int overlap = 0; // 用于记录与当前点重合的点数
HashMap<Double, Integer> slopeMap = new HashMap<>(); // 用于存储斜率与点数的映射
for (int j = 0; j < points.length; j++) {
if (i == j) {
overlap++; // 与自身重合的点数加1
} else {
double slope;
if (points[i][0] == points[j][0]) {
slope = Double.POSITIVE_INFINITY; // 当x坐标相同时,斜率设为正无穷大
} else {
slope = (double)(points[i][1] - points[j][1]) / (points[i][0] - points[j][0]); // 计算斜率
}
slopeMap.put(slope, slopeMap.getOrDefault(slope, 0) + 1); // 存储斜率并更新点数
}
}
int localMax = overlap; // 初始化局部最大点数为与自身重合的点数
for (int count : slopeMap.values()) {
localMax = Math.max(localMax, count + overlap); // 更新局部最大点数
}
maxPoints = Math.max(maxPoints, localMax); // 更新全局最大点数
}
return maxPoints;
}
}
这段代码通过哈希表来统计每个点的斜率,然后记录直线上的点数,最终找到直线上点数最多的情况。
解2
除了上述的哈希表解法外,还有一种更优化的解法,可以在O(n^2)的时间内解决问题,其中n是点的数量。
这个解法基于以下观察:如果有三个点共线,那么它们的斜率是相同的。因此,我们可以遍历每一对点,计算它们之间的斜率,并存储在哈希表中。对于每个点,我们统计共线的点的数量,并保持更新最大值。
以下是基于这种观察的Java代码:
class Solution {
public int maxPoints(int[][] points) {
if (points.length < 3) {
return points.length;
}
int maxPoints = 2; // 初始化最大点数为2,因为至少有两个点在同一直线上
for (int i = 0; i < points.length; i++) {
int overlap = 0; // 用于记录与当前点重合的点数
HashMap<String, Integer> slopeMap = new HashMap<>(); // 用于存储斜率与点数的映射
for (int j = 0; j < points.length; j++) {
if (i == j) {
overlap++; // 与自身重合的点数加1
} else {
int deltaX = points[i][0] - points[j][0];
int deltaY = points[i][1] - points[j][1];
if (deltaX == 0) {
slopeMap.put("inf", slopeMap.getOrDefault("inf", 0) + 1); // 斜率为正无穷
} else {
int gcd = gcd(deltaX, deltaY);
String slope = (deltaY / gcd) + "/" + (deltaX / gcd); // 用字符串表示斜率
slopeMap.put(slope, slopeMap.getOrDefault(slope, 0) + 1);
}
}
}
int localMax = overlap; // 初始化局部最大点数为与自身重合的点数
for (int count : slopeMap.values()) {
localMax = Math.max(localMax, count + overlap); // 更新局部最大点数
}
maxPoints = Math.max(maxPoints, localMax); // 更新全局最大点数
}
return maxPoints;
}
// 辗转相除法计算最大公约数
private int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
}
这种解法避免了使用浮点数斜率,使用最大公约数来保持斜率的精度,同时也处理了斜率为正无穷的情况。这个解法的时间复杂度为O(n^2),但在实际应用中通常更高效。
解3
动态规划的思路是,对于每个点 (xi, yi),可以考虑以它为终点的直线上的点数,然后记录最大值。下面是一个使用动态规划的Java代码示例:
class Solution {
public int maxPoints(int[][] points) {
if (points.length < 3) {
return points.length;
}
int maxPoints = 2; // 初始化最大点数为2,因为至少有两个点在同一直线上
int n = points.length;
for (int i = 0; i < n; i++) {
int overlap = 0; // 用于记录与当前点重合的点数
int localMax = 0; // 用于记录以当前点为终点的直线上的点数
HashMap<String, Integer> slopeMap = new HashMap<>(); // 用于存储斜率与点数的映射
for (int j = i + 1; j < n; j++) {
int deltaX = points[i][0] - points[j][0];
int deltaY = points[i][1] - points[j][1];
if (deltaX == 0 && deltaY == 0) {
overlap++; // 与自身重合的点数加1
} else {
int gcd = gcd(deltaX, deltaY);
String slope = (deltaY / gcd) + "/" + (deltaX / gcd); // 用字符串表示斜率
slopeMap.put(slope, slopeMap.getOrDefault(slope, 0) + 1); // 存储斜率并更新点数
localMax = Math.max(localMax, slopeMap.get(slope)); // 更新以当前点为终点的直线上的点数
}
}
maxPoints = Math.max(maxPoints, localMax + overlap + 1); // 更新全局最大点数,加1是因为还包括自身点
}
return maxPoints;
}
// 辗转相除法计算最大公约数
private int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
}