聚类是机器学习中一种重要的无监督算法,可以将数据点归结为一系列的特定组合。归为一类的数据点具有相同的特性,而不同类别的数据点则具有各不相同的属性。
11.1 聚类算法介绍
人们将物理或抽象对象的集合分成由类似 的对象组成的多个类的过程被称为聚类。
11.1.1 聚类是什么
聚类和降维之间有着共通性, 某种意义上聚类就是降维,聚成 K 类就意味着将原来的数据降为 K 维。分类与聚类虽然名称较为接近但两者截然不同,分类是有监督学习中的典型问题,而聚类则是无监督学习中的典型问题。
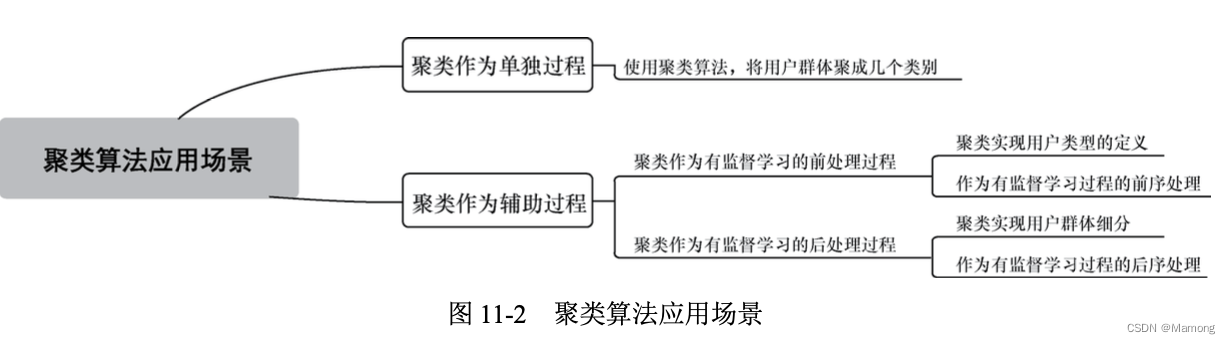
11.1.2 聚类算法应用场景
11.2 通俗讲解聚类算法过程
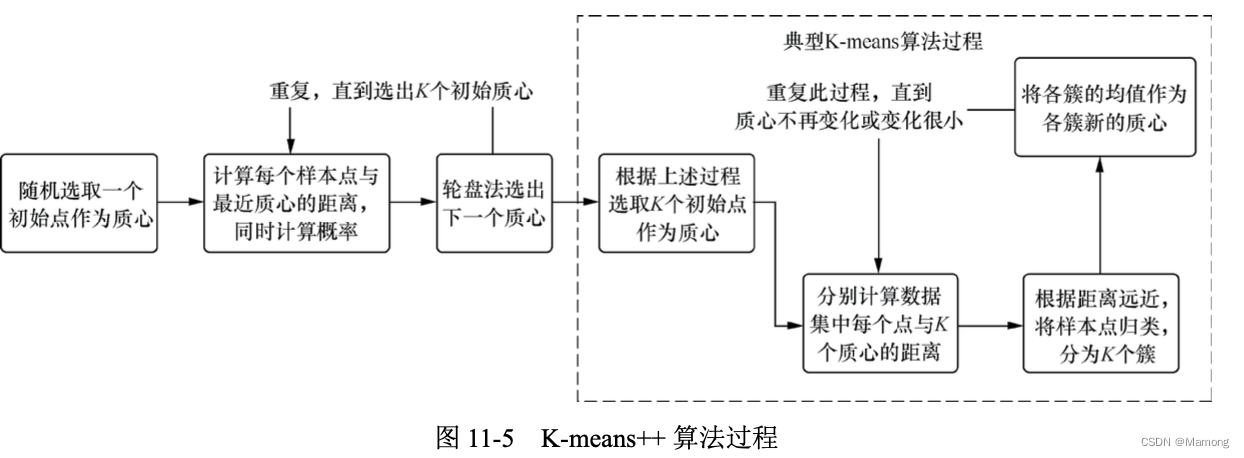
聚类算法是无监督学习的典型算法,其中 K-means 算法又是聚类算法中的经典算法。 K-means 算法要求预先设定聚类的个数,然后不断更新聚类中心,通过多次迭代最终使得所有数据点到其聚类中心距离的平方和趋于稳定。
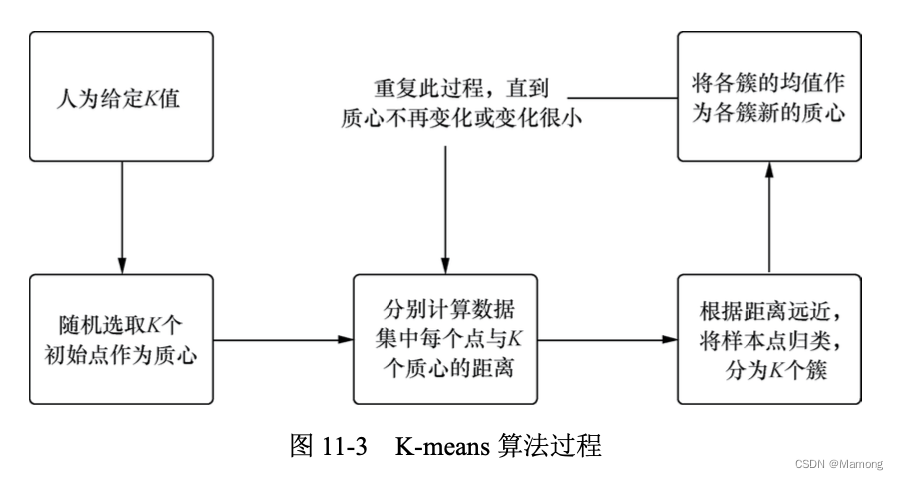
一般来说,K-means 聚类过程如下所示。
(1)从 n 个向量对象中任意选择 K 个对象作为初始聚类中心。
(2)根据步骤(1)中设置的 K 个聚类中心,分别计算每个对象与这 K 个聚类中心对象的距离。
(3)经过步骤(2)后,任何一个对象与这 K 个聚类中心都有一个距离值。这些距离有的远, 有的近,将对象与距离它最近的聚类中心归为一类。
(4)重新计算每个类簇的聚类中心。 (5)重复步骤(3)和步骤(4),直到对象归类变化量极小或者完全停止变化。例如,某次
迭代后只有不到 1% 的对象还会出现类簇之间的归类变化,就可以认为聚类算法实现了。
有两个需要注意的关键点:一是对象距离如何度量;二是聚类效果如何评估,也就是性能如何度量。
11.2.1 相似度如何度量
“相似度”就是通过距离来表示。最常见的距离是“闵可夫斯基距离”: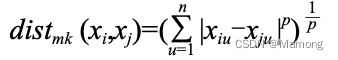
除了常用的闵可夫斯基距离之外,还有雅卡尔相似系数、余弦相似度、相对熵、黑林格距
离等多种距离计算方法。
11.2.2 聚类性能如何度量
(1)数据含有标记信息。使用调整兰德系数(Adjusted Rand Index,ARI)指标。ARI 指标和分类问题中的准确率指标比较类似,在 sklearn 的 metrics 里面就可以调用。
(2)数据不含标记信息。使用轮廓系数来度量聚类效果。轮廓系数具有兼顾聚类的凝聚度和分离度的优点,数值为 [-1,1]。一般来说,轮廓系数越大,聚类效果越好。轮廓系数可以通过在 sklearn 的 metrics 中调用 silhouette_score 来实现。
11.2.3 具体算法介绍:K-means算法
对于 K-means 算法 中 K 的选取,目前有一种称为“Elbow Method”的方法来处理:通过绘制 K-means 代价函数与 聚类数目 K 的关系图,选取直线拐点处的 K 值作为最佳的聚类中心数目。
但实际中更为常见和提倡的做法还是算法工程师从实际问题出发人工指定合理的 K 值,通过多次随机初始化聚类中心选取比较满意的结果。
K-means 算法是初值敏感的,也就是起始时选择不同的点作为质心,最后得到的聚类结果 可能是不同的。K-means++ 算法就此问题进行了改进。
11.2.4 具体算法介绍:K-means++算法
K-means++ 算法的核心思想是,初始质心并不随机选取,而是希望这 K 个初 始质心相互之间分得越开越好。
计算每个样本点与当前已有质心的最短距离(即与最近一个质心的距离),用![]() 表示;接着计算每个样本点被选中作为下一个质心的概率,用
表示;接着计算每个样本点被选中作为下一个质心的概率,用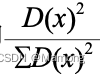 表示。值越大表示该点被选为质心的概率越大。这个用概率选取质心的方法就是轮盘法。
表示。值越大表示该点被选为质心的概率越大。这个用概率选取质心的方法就是轮盘法。
轮盘法
我们来看一下如何根据权重来确定概率,实现这点的算法有很多,其中比较简单的是轮盘法。这个算法应该源于赌博或者是抽奖,原理也非常相似。
我们或多或少都玩过超市或者是其他场景下的转盘抽奖,在抽奖当中有一个指针一直保持不动。我们转动转盘,当转盘停下的时候,指针所指向的位置就是抽奖的结果。
我们都知道命中结果的概率和轮盘上对应的面积有关,面积越大抽中的概率也就越大,否则抽中的概率越小。
我们用公式表示一下,对于每一个点被选中的概率是:
其中是每个点到所有类簇的最短距离,表示点被选中作为类簇中心的概率。
轮盘法其实就是一个模拟转盘抽奖的过程,只不过我们用数组模拟了转盘。我们把转盘的扇形拉平,拉成条状,原来的每个扇形就对应了一个区间。扇形的面积就对应了区间的长度,显然长度越长,抽中的概率越大。然后我们来进行抽奖,我们用区间的长度总和乘上一个0-1区间内的数。
我们找到这个结果落在的区间,就是这次轮盘抽中的结果。这样我们就实现了控制随机每个结果的概率。
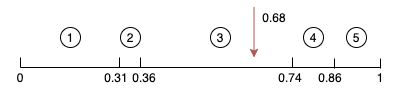
在上面这张图当中,我们随机出来的值是0.68,然后我们一次减去区间,最后落到的区间。
11.3 编程实践:手把手教你写代码
参考:
详解Kmeans的两大经典优化,mini-batch和kmeans++-腾讯云开发者社区-腾讯云