【图像分类】【深度学习】【Pytorch版本】VggNet模型算法详解
文章目录
- 【图像分类】【深度学习】【Pytorch版本】VggNet模型算法详解
- 前言
- VggNet讲解
- 感受野
- 感受野的计算公式
- 3x3的卷积核的使用
- VggNet模型结构
- VGGnet Pytorch代码
- 完整代码
- 总结
前言
Vgg(Visual Geometry Group)是由牛津大学的Simonyan, Karen等人在《Very deep convolutional networks for large-scale image recognition【ICLR-2015】》【论文地址】一文中提出的模型,核心思想是通过使用小尺寸的卷积核(通常为3x3),来代替较大感受野的卷积层,通过重复堆叠多个卷积块来增加网络深度,并通过逐渐减小特征图尺寸和增加特征通道数来扩展网络规模。
VggNet讲解
感受野
感受野(Receptive Field)是指在神经网络中,每个网络层输出的特征图中的一个像素点映射回原始输入图像中的区域大小,网络层越深,其输出特征的元素对应感受野越大。

在卷积神经网络(CNN)和全连接神经网络(FCN)中,感受野的计算和作用存在区别:
- 在全连接神经网络中,其输出的每个特征都受到所有输入特征影响,每个神经元都与所有输入特征相连接,全连接层中的每个神经元都可以感知整个输入特征的信息,全连接网络可以对输入数据进行全局建模。
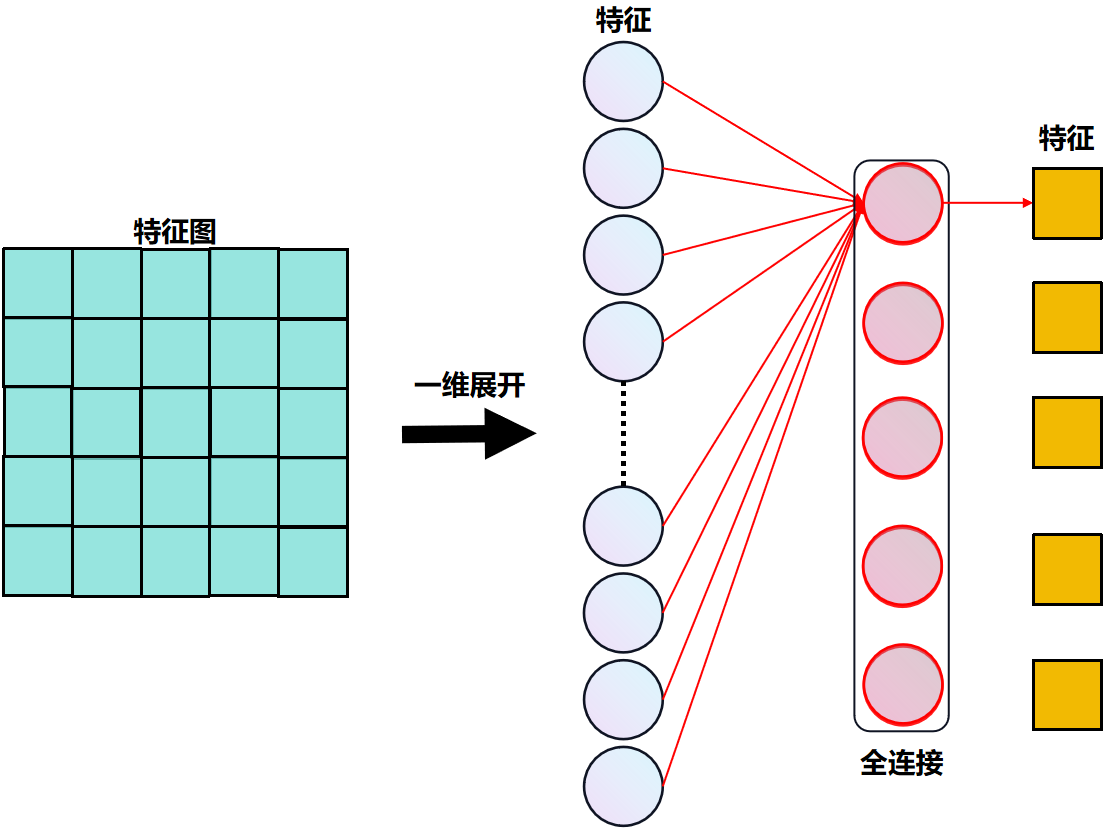
全连接层通常用于网络的最后几层,用于对从卷积层中提取的局部特征进行整合和分类。
- 在卷积神经网络中,其输出的特征图(feature map)上的每个像素特征只受到输入特征图上局部区域影响,每个神经元每次只与输入特征图上局部区域相连接,局部区域大小为卷积核的大小,卷积层中的每个神经元只可以感知局部输入特征的信息,因此卷积神经网络需要多层卷积层的堆叠使得网络能够逐渐扩大感受野,从而捕捉到更大范围的特征信息。

卷积层中的每个神经元只能感知输入特征图的局部区域,如绿色特征图的某像素特征(红色方块)在青蓝色特征图上的感受野(红色方框),通过多个神经元的组合,卷积神经网络可以提取输入图像的全局特征,如黄色特征图的像素特征就能完整获取青蓝色特征图的所有信息。这种局部感知的特性使得卷积神经网络在图像处理和计算机视觉任务中表现出色。
感受野的计算公式
卷积神经网络通过大量的卷积层、归一化层、激活层和池化层进行堆叠构成完整的网络结构,而卷积层和池化均会改变特征图的大小,从而实现特征之间的映射和转换,因此卷积核或池化核(kernel_size)、和步长(stride)参数共同决定了输出结果对应的感受野大小。
k
n
{k_n}
kn、
s
n
{s_n}
sn、
r
n
{r_n}
rn分别表示第
n
n
n层的卷积核尺寸、步长和感受野。卷积神经网络的感受野计算公式在表达上有些许的差异,博主给出了不同的公式表达的含义:
- 自底向上的方式: r n = r n − 1 + ( k n − 1 ) Π i = 1 n − 1 s i {r_n} = {r_{n - 1}} + ({k_n} - 1)\Pi _{i = 1}^{n - 1}{s_i} rn=rn−1+(kn−1)Πi=1n−1si其中 n ≥ 2 , r 0 = 1 , r 1 = k 1 n \ge 2,{r_0} = 1,{r_1} = k_1 n≥2,r0=1,r1=k1。
- 自顶向下的方式: r n = ( r n + 1 − 1 ) s i + k {r_n} = ({r_{n + 1}} - 1){s_i} + k rn=(rn+1−1)si+k其中 r n = 1 {r_n} = 1 rn=1。
博主将通过一个案例详细说明俩种方法的区别,如下图所示,原始图像输入
r
0
=
7
×
7
{r_0}=7×7
r0=7×7,假设共经历3个卷积层:此时三个卷积层的输出依次为
r
1
=
5
×
5
{r_1}=5×5
r1=5×5 ,
r
2
=
3
×
3
{r_2}=3×3
r2=3×3 和
r
3
=
1
×
1
{r_3}=1×1
r3=1×1 。

说明俩种方法计算感受野的区别如下表所示:
| 自底向上 | 自顶向下 |
|---|---|
| n n n个网络层输出的特征图分别在原始图像上的感受野大小 | 第 n n n层网络输出的特征图分别在前 n n n层特征图上的感受野大小 |
| r 0 = 1 {r_0}=1 r0=1 | Conv(3): r 3 = 1 {r_3}=1 r3=1 |
| Conv(1): r 1 = 3 {r_1}=3 r1=3 | Conv(2): r 2 = ( 1 − 1 ) × 1 + 3 = 3 {r_2}=(1-1)×1+3=3 r2=(1−1)×1+3=3 |
| Conv(2): r 2 = 3 + ( 3 − 1 ) × 1 = 5 {r_2}=3+(3-1)×1=5 r2=3+(3−1)×1=5 | Conv(1): r 1 = ( 3 − 1 ) × 1 + 3 = 5 {r_1}=(3-1)×1+3=5 r1=(3−1)×1+3=5 |
| Conv(3): r 2 = 5 + ( 3 − 1 ) × 1 = 7 {r_2}=5+(3-1)×1=7 r2=5+(3−1)×1=7 | r 0 = ( 3 − 1 ) × 1 + 5 = 7 {r_0}=(3-1)×1+5=7 r0=(3−1)×1+5=7 |
假设都是计算第三个卷积层的输出特征图像素点在原始输入图像上的感受野,二者的大小是一致的。
3x3的卷积核的使用
3x3 卷积核是能够感受到上下、左右、重点的最小的感受野尺寸,论文中提到,堆叠两个3x3的卷积核的感受野等同于1个5x5的卷积核,堆叠三个3x3的卷积核的感受野等同于1个7x7的卷积核,并且使用3x3卷积核替换后可以减少参数。由于感受野相同,3个3x3的卷积,使用了3个非线性激活函数,增加了非线性表达能力。
| 卷积核尺寸 | 卷积核感受野 | 卷积核参数(假设输入输出channel为C) |
|---|---|---|
| 3×3 | r 1 = 3 {r_1}=3 r1=3, r 2 = 3 + ( 3 − 1 ) × 1 = 5 {r_2}=3+(3-1)×1=5 r2=3+(3−1)×1=5, r 2 = 5 + ( 3 − 1 ) × 1 = 7 {r_2}=5+(3-1)×1=7 r2=5+(3−1)×1=7 | 3×3×C×C= 9 C 2 9{C^2} 9C2, 18 C 2 18{C^2} 18C2, 27 C 2 27{C^2} 27C2 |
| 5×5 | r 1 = 5 {r_1}=5 r1=5 | 5×5×C×C= 25 C 2 25{C^2} 25C2> 18 C 2 18{C^2} 18C2 |
| 7×7 | r 1 = 7 {r_1}=7 r1=7 | 7×7×C×C= 49 C 2 49{C^2} 49C2> 27 C 2 27{C^2} 27C2 |
总而言之,使用3x3卷积核堆叠的形式,既增加了网络层数又减少了参数量。
VggNet模型结构
下图是原论文给出的关于VGGnet模型结构的详细示意图:

注:卷积层的参数卷积层的参数被表示为"卷积场大小-通道数",ReLU激活函数在表中没有显示
与AlexNet⼀样,VggNet可以分为两部分:第⼀部分 (backbone) 主要由卷积层和池化层(汇聚层)组成,第⼆部分由全连接层 (分类器) 组成。
| VggNet的亮点 | 说明 |
|---|---|
| 小卷积核 | 堆叠多个3×3的卷积核来替代大的卷积核,部分使用1x1卷积核的(C结构网络中),以减少所需参数 |
| 小池化核 | 全部为2×2的池化核 |
| 更深更宽的网络结构 | 卷积核专注于扩大通道数,池化专注于缩小高和宽,使得模型更深更宽的同时,计算量的增加不是很剧烈 |
| 去掉了LRN层 | LRN浪费了更多的内存和时间并且性能没有太大提升 |
VGG的预训练权重是使用ImageNet数据集进行训练而来:
# 官方的预训练权重
model_urls = {
'vgg11': 'https://download.pytorch.org/models/vgg11-bbd30ac9.pth',
'vgg13': 'https://download.pytorch.org/models/vgg13-c768596a.pth',
'vgg16': 'https://download.pytorch.org/models/vgg16-397923af.pth',
'vgg19': 'https://download.pytorch.org/models/vgg19-dcbb9e9d.pth'
}
VGGnet Pytorch代码
backbone部分
# VGGnet的四种网络配置
cfgs = {
'vgg11': [64, 'M', 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'],
'vgg13': [64, 64, 'M', 128, 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'],
'vgg16': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 'M', 512, 512, 512, 'M', 512, 512, 512, 'M'],
'vgg19': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 256, 'M', 512, 512, 512, 512, 'M', 512, 512, 512, 512, 'M'],
}
def make_features(cfg: list):
layers = []
# RGB图像3通道
in_channels = 3
for v in cfg:
# 池化层
if v == "M":
# 全部为2×2的池化核
layers += [nn.MaxPool2d(kernel_size=2, stride=2)]
else:
# 卷积层组:conv2d+ReLU
conv2d = nn.Conv2d(in_channels, v, kernel_size=3, padding=1)
layers += [conv2d, nn.ReLU(True)]
in_channels = v
return nn.Sequential(*layers)
分类器部分
# 分类器部分:FC+ReLU+Dropout
self.classifier = nn.Sequential(
nn.Linear(512*7*7, 4096),
nn.ReLU(True),
nn.Dropout(p=0.5),
nn.Linear(4096, 4096),
nn.ReLU(True),
nn.Dropout(p=0.5),
nn.Linear(4096, num_classes)
)
完整代码
import torch.nn as nn
import torch
from torchsummary import summary
# 官方的预训练权重
model_urls = {
'vgg11': 'https://download.pytorch.org/models/vgg11-bbd30ac9.pth',
'vgg13': 'https://download.pytorch.org/models/vgg13-c768596a.pth',
'vgg16': 'https://download.pytorch.org/models/vgg16-397923af.pth',
'vgg19': 'https://download.pytorch.org/models/vgg19-dcbb9e9d.pth'
}
class VGG(nn.Module):
def __init__(self, features, num_classes=1000, init_weights=False):
super(VGG, self).__init__()
# backbone部分
self.features = features
# 分类器部分:FC+ReLU+Dropout
self.classifier = nn.Sequential(
nn.Linear(512*7*7, 4096),
nn.ReLU(True),
nn.Dropout(p=0.5),
nn.Linear(4096, 4096),
nn.ReLU(True),
nn.Dropout(p=0.5),
nn.Linear(4096, num_classes)
)
# 对模型的权重进行初始化操作
if init_weights:
self._initialize_weights()
def forward(self, x):
# N x 3 x 224 x 224
x = self.features(x)
# N x 512 x 7 x 7
x = torch.flatten(x, start_dim=1)
# N x 512*7*7
x = self.classifier(x)
return x
def _initialize_weights(self):
for m in self.modules():
if isinstance(m, nn.Conv2d):
# Conv2d的权重从均匀分布中随机初始化
nn.init.xavier_uniform_(m.weight)
if m.bias is not None:
# Conv2d的偏置置0
nn.init.constant_(m.bias, 0)
elif isinstance(m, nn.Linear):
# FC的权重从均匀分布中随机初始化
nn.init.xavier_uniform_(m.weight)
# FC的偏置置0
nn.init.constant_(m.bias, 0)
def make_features(cfg: list):
layers = []
# RGB图像3通道
in_channels = 3
for v in cfg:
# 池化层
if v == "M":
# 全部为2×2的池化核
layers += [nn.MaxPool2d(kernel_size=2, stride=2)]
else:
# 卷积层组:conv2d+ReLU
conv2d = nn.Conv2d(in_channels, v, kernel_size=3, padding=1)
layers += [conv2d, nn.ReLU(True)]
in_channels = v
return nn.Sequential(*layers)
# VGGnet的四种网络配置
cfgs = {
'vgg11': [64, 'M', 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'],
'vgg13': [64, 64, 'M', 128, 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'],
'vgg16': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 'M', 512, 512, 512, 'M', 512, 512, 512, 'M'],
'vgg19': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 256, 'M', 512, 512, 512, 512, 'M', 512, 512, 512, 512, 'M'],
}
def vgg(model_name="vgg16", **kwargs):
assert model_name in cfgs, "Warning: model number {} not in cfgs dict!".format(model_name)
cfg = cfgs[model_name]
model = VGG(make_features(cfg), **kwargs)
return model
if __name__ == '__main__':
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
model = vgg("vgg16").to(device)
summary(model, input_size=(3, 224, 224))
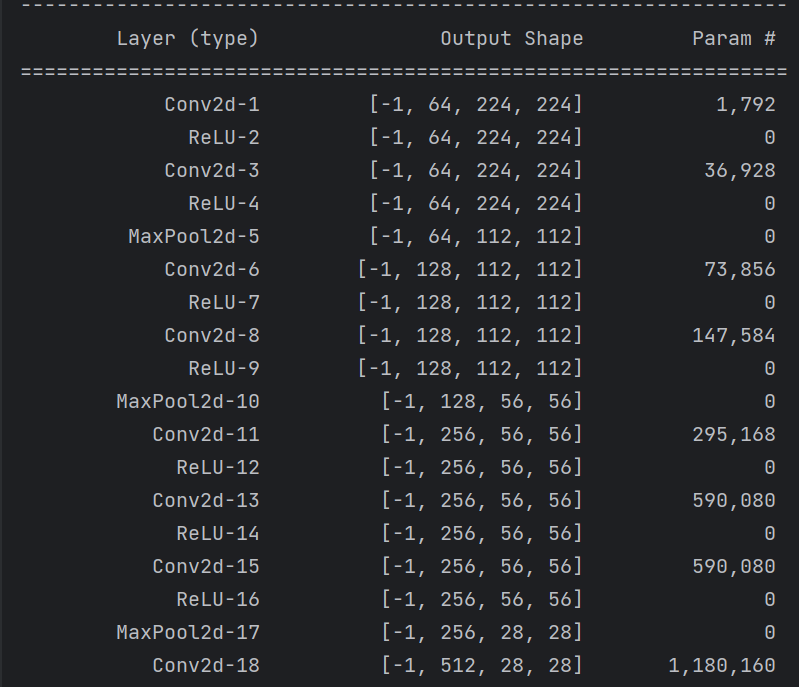
summary可以打印网络结构和参数,方便查看搭建好的网络结构。
总结
尽可能简单、详细的介绍了深度可分卷积的原理和卷积过程,讲解了VGGnet模型的结构和pytorch代码。