2022ICPC，济南站（M，E，D

news2024/11/25 14:33:44

初见安~好久好久没写博客了……感觉还是有必要写的。

拿去年济南的题目训练了一下，状态还不错，写一下自己写过了的题目的题解。

M Best Carry Player

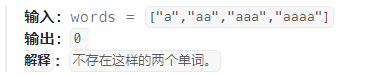
题意：给你n $(1 \leq n \leq 10^5)$ 个数，交换他们的顺序使依次相加后总的进位次数最少（十进制），并输出进位次数。 $(1 \leq a_i \leq10^9)$

很显然，加法中两数相加最多进位进1；单看每一位就能发现，其实进位次数跟顺序压根没关系。

所以写一个高精加法模拟加法过程算进位次数就完了。

注意数据范围，最多可以达到14位数。

#include<algorithm>
#include<iostream>
#include<iomanip>
#include<cstring>
#include<cstdio>
#include<vector>
#include<cmath>
#include<queue>
#include<map>
using namespace std;
typedef long long ll;
int read() {
	int x = 0, f = 1, ch = getchar();
	while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();}
	while(isdigit(ch)) x = (x << 1) + (x << 3) + ch - '0', ch = getchar();
	return x * f;
}

int T, n;
int res[100];
char s[100];
signed main() {
	T = read();
	while(T--) {
		memset(res, 0, sizeof res);
		n = read(); int ans = 0;
		for(int i = 1; i <= n; i++) {
			scanf("%s", s + 1); int len = strlen(s + 1), p = 1;
			for(int j = len; j; j--, p++) {
				res[p] += s[j] - '0';
				if(res[p] > 9) res[p] -= 10, ans++, res[p + 1]++;
			}
			
			for(; p <= 15; p++) if(res[p] > 9) res[p] -= 10, ans++, res[p + 1]++;//
		}
		printf("%d\n", ans);
	}
	return 0;
}
/*
2
3
9 99 999
1
12345
*/

E Identical Parity

题意：T $(1 \leq T \leq 10^5)$ 组数据，每次给定一个n和k $(1 \leq k \leq n \leq 10^9)$ ，问是否存在一个n的排列，满足所有长度为k的子区间内的数的和的奇偶性相同。

显然我们只需要考虑这长度为n的排列中每个数的奇偶个数能否满足。

有一些特殊情况容易想到：

k=1时，除非n=1，否则都无法满足题意；
k为偶数时，一定可以满足题意（奇偶交错的排列均可）；
k为奇数(k != 1)时，我们需要额外进行讨论了。

因为若长度为n的排列是满足奇偶性的条件，那么任意长度为l $(k \leq l \leq n)$ 的区间都满足区间奇偶性的条件。（不一定满足为一个合法排列，即奇数个数=偶数个数（+1）的条件）所以我们首要考虑奇偶性的条件如何满足。

首先考虑第一个长度为k的区间，k是奇数，故一定是奇数个数大于偶数个数（否则凑不了多少长度），不妨令x+1为奇数个数，则x为偶数个数。（2x+1=k）

令此时的构造排列为 $\left \{ x_i \right \}$ ，其中xi为0或者1表示为偶数or奇数。

假设我们已经构造好了 $x_1,...x_k$ ，对于下一个区间 $x_2...x_{k+1}$ ，相当于在前一个区间的基础上减去x1加上x_{k+1}，且sum的奇偶性不变。换言之， $x_1$ 与 $x_{k+1}$ 奇偶性相同。也就是说：对于任意长度的排列，我们构造好了前k个的奇偶性后，之后每一位的奇偶性都是确定的。也可以说：每个区间内奇数和偶数个数都是一样的。

所以我们只需要考虑如何对这x+1个奇数和x个偶数如何进行排序。

易知n=2k时，即奇数比偶数多两个，一定无法构造出来；推出n=tk时，奇数会比偶数多t个。所以要满足题意，我们需要在后面补至少t-1个偶数。也就是说此时构造的x序列，至少前t-1个可以是偶数。即： $t-1\leq x$ 。

同理，假如我们补完所有0后继续往后面补1，至多可以补多少个1呢？那就是 $x-(t-1)$ 个，也就是多了多少个0就可以补多少个1。

所以我们可以得出当 $n \in[tk, (t+1)k]$ 时，只有 $n \in [tk+t-1,tk+x+x-(t-1)]$ 时构造有解。

举个例子：k=3时，我们容易想到n=3,4,5都构造有解。而n=7就是最大的一个满足情况的n。

我们只能构造奇偶序列如：011 011 0，把0放在最前面，这样会优先把0复制在最后。

再比如k=5时，我们可以构造前5个为00111，这样可以满足n=11~13，17的情况。

代码就是公式抄一遍。

#include<algorithm>
#include<iostream>
#include<iomanip>
#include<cstring>
#include<cstdio>
#include<vector>
#include<cmath>
#include<queue>
#include<map>
using namespace std;
typedef long long ll;
int read() {
	int x = 0, f = 1, ch = getchar();
	while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();}
	while(isdigit(ch)) x = (x << 1) + (x << 3) + ch - '0', ch = getchar();
	return x * f;
}

int T, n, k;
signed main() {
	T = read();
	while(T--) {
		n = read(), k = read();
		if(k == 1) {
			if(n == 1) puts("Yes");
			else puts("No");
		}
		else if(k % 2 == 0) puts("Yes");
		else {
			int t = n / k, x = k / 2;
			if(t * k + t - 1 <= n && n <= t * k + 2 * x - t + 1) puts("Yes");
			else puts("No");
		}
	}
	return 0;
}

D Frozen Scoreboard

题意：

（bushi）

n个题目m个队伍，你有一个封榜前的榜单，已知每个队伍（相互独立）每个题目的状态和最终通过提数和罚时，问你是否存在一个终榜满足这些条件并构造出来。（具体的看原题目吧）

说白了就是模拟……没通过和没提交的题目没有任何作用，原样输出就好；+的题目要记得加上wa的罚时，剩下的就是？的题目看要选哪些通过。

n很小啊只有13，那就最多13个？。我们把？全取出来，需要通过的题目数是已知的，最坏情况是 $C_{13}^7=1716$ ，m又只有1e3，所以暴力枚举。枚举完了过后考虑如何分配剩余的罚时。

首先每个题目240罚时起步；其次20，20地尽量把赛后的未通过提交的罚时用完，最后再用每个题剩的59min去凑零碎的剩余罚时。

思路很简单但是实现起来挺恶心的……要存的东西很多。

以及对于No的判定，要提前把？不够多；罚时不够减；罚时凑不上等一看就凑不出来的情况判掉。

上代码了

#include<algorithm>
#include<iostream>
#include<iomanip>
#include<cstring>
#include<cstdio>
#include<vector>
#include<cmath>
#include<queue>
#include<map>
using namespace std;
typedef long long ll;
int read() {
	int x = 0, f = 1, ch = getchar();
	while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();}
	while(isdigit(ch)) x = (x << 1) + (x << 3) + ch - '0', ch = getchar();
	return x * f;
}

int n, m;
int num, T; 
struct node {
	char x;
	int cnt, tm;
}st[20];

struct TSK {
	int cnt, tm;
	int out_cnt, out_tm;
	bool in;
}tsk[20];

int tot = 0;
bool flag;
int ch[20];
void out() {
	puts("Yes");
	int now = 1;
	for(int i = 1; i <= m; i++) {
		if(st[i].x == '.') puts(".");
		else if(st[i].x == '-') printf("- %d\n", st[i].cnt);
		else if(st[i].x == '+') printf("+ %d/%d\n", st[i].cnt, st[i].tm);
		else {
			if(tsk[now].in) printf("+ %d/%d\n", tsk[now].out_cnt, tsk[now].out_tm);
			else printf("- %d\n", tsk[now].cnt);
			now++;
		}
	}
}

void dfs(int p, int lst) {
	if(flag) return;
	if(p > tot && lst <= num) return;
	if(lst > num) {//通过数凑到了
		int Tm = T - 240 * num;//每个题至少240罚时
		for(int i = 1; i <= num; i++) {
			tsk[ch[i]].out_tm = 240, Tm -= (tsk[ch[i]].cnt - tsk[ch[i]].tm) * 20;
			tsk[ch[i]].out_cnt = tsk[ch[i]].cnt - tsk[ch[i]].tm + 1;
			if(tsk[ch[i]].out_cnt > tsk[ch[i]].cnt) return;
		}
		if(Tm < 0) return;//必扣罚时扣了发现时间不够

		for(int i = 1; i <= num && Tm > 20; i++) {
			register int cnt1 = tsk[ch[i]].cnt, cnt2 = tsk[ch[i]].out_cnt;
			if(Tm > (tsk[ch[i]].tm - 1) * 20) Tm -= (tsk[ch[i]].tm - 1) * 20, tsk[ch[i]].out_cnt = tsk[ch[i]].cnt;
			else {
				int tmp = Tm / 20;
				Tm -= tmp * 20;
				tsk[ch[i]].out_cnt += tmp;
			}
		}
		for(int i = 1; i <= num && Tm > 0; i++) {
			if(Tm > 59) Tm -= 59, tsk[ch[i]].out_tm = 299;
			else if(Tm > 0) tsk[ch[i]].out_tm += Tm, Tm = 0;
		}
		
		if(!Tm) {flag = true; out();}
		return;
	}
	dfs(p + 1, lst);
	if(flag) return;
	tsk[p].in = true; ch[lst] = p; dfs(p + 1, lst + 1); tsk[p].in = false;
}

signed main() {
//	freopen("out.txt", "w", stdout);
	n = read(), m = read();
	while(n--) {
		num = read(), T = read();
		tot = 0; int sum = 0;
		flag = false;
		for(int i = 1; i <= m; i++) {
			cin >> st[i].x;
			if(st[i].x == '.') continue;
			else if(st[i].x == '-') st[i].cnt = read();
			else if(st[i].x == '+') {
				int t1 = read(), t2 = read();
				st[i].cnt = t1, st[i].tm = t2;
				T -= (t2 + t1 * 20 - 20);
				num--;
			} else {
				st[i].tm = tsk[++tot].tm = read(),//tm: after frozen
				st[i].cnt = tsk[tot].cnt = read();//cnt: all of
				tsk[tot].in = false;
				sum += st[i].cnt - 1;//sum:至多凑出来的罚时次数（其实作用不大
			}
		}
		
		if(num < 0 || T < 0 || tot < num || num * 240 > T || num * 299 + sum * 20 < T) 
			{puts("No"); continue;}
			
		dfs(1, 1);
		if(!flag) puts("No");
	}
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1176159.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！