一文搞懂优先队列及相关算法

大家好，我是方圆。优先队列在 Java 中的定义是 PriorityQueue，它基于 二叉堆 数据结构实现，其中的元素并不是全部有序，但它能够支持高效地 获取或删除最值元素。

二叉堆是一种特定条件的 完全二叉树，树的根节点为堆顶，最右端叶子节点为堆底，分为 小顶堆 和 大顶堆。小顶堆堆顶元素最小，且任意节点小于等于其子节点，大顶堆堆顶元素最大，且任意节点大于等于其子节点，如下图所示：

堆.jpg

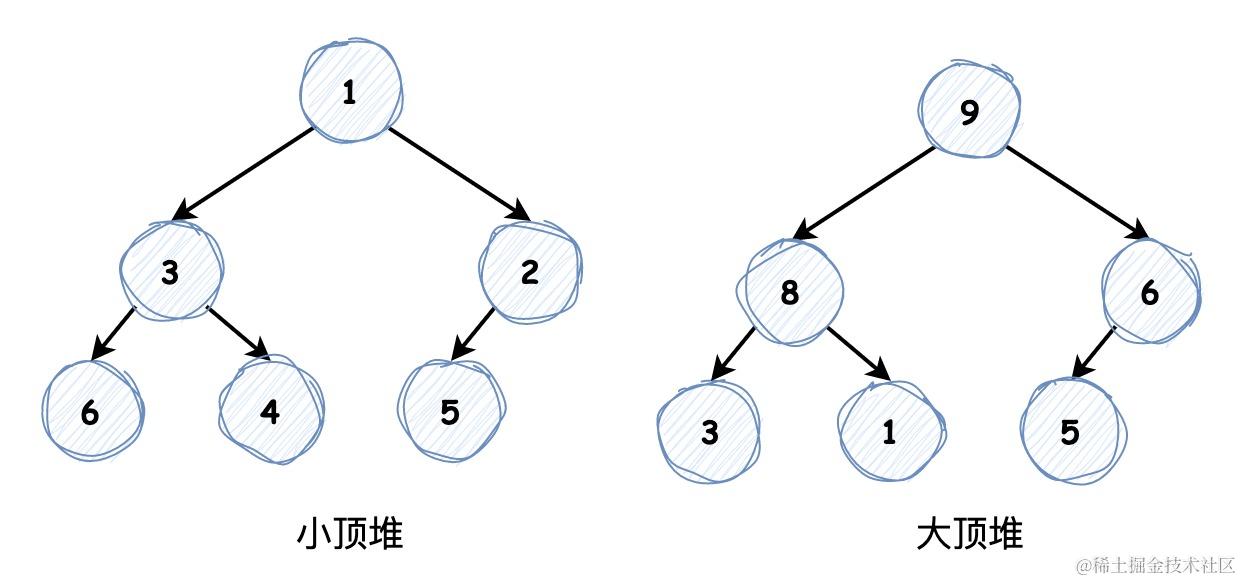
完全二叉树只有叶子节点未被填满，且叶子节点从左向右进行填充。

优先队列可以用于解决 TOP-K 问题 和 中位数问题，下面我们先来看一些练习。如果大家想要找刷题路线的话，可以参考 Github: LeetCode。

TOP-K 问题

TOP-K 问题是求最大/最小的 K 个值，解题思路很简单：以求最大的 K 个值为例，我们需要建立一个最多容纳 K 个值的小顶堆，并不断将元素入堆，直到优先队列中的元素数量为 K 时，后续再有元素入堆则需要判断它与堆顶元素的大小关系，如果它比堆顶元素大，那么堆顶元素出堆，再将这个新元素插入堆中，如此反复直到所有元素遍历完毕，最后堆顶元素即为第 K 大元素。

这个解题思路可以归纳为模板：用小顶堆解决第 K 大问题，用大顶堆解决第 K 小问题，解决第 K 大问题代码如下，供大家参考：

    public int findKthLargest(int[] nums, int k) {
        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();

        for (int num : nums) {
            if (priorityQueue.size() < k) {
                priorityQueue.offer(num);
            } else {
                if (num > priorityQueue.peek()) {
                    priorityQueue.poll();
                    priorityQueue.offer(num);
                }
            }
        }

        return priorityQueue.peek();
    }

当然排序也能够解决 TOP-K 问题，但是如果数组元素过多，比如在 10 亿个数中取其中第 10 大元素，我们真的想把这 10 亿个数排序吗？这 10 亿个数能一下装进内存吗？但如果我们使用了优先队列，仅需要维护一个存储 10 个元素的优先队列即可

小顶堆

215. 数组中的第K个最大元素

本题是典型的应用小顶堆解决第K大元素的问题，大家直接按照解题模板解题即可。

703. 数据流中的第 K 大元素

大家解完上一题再拿这题练练手。

692. 前K个高频单词

本题相对来说没有那么容易，但是本质是一样的，我们来一起看一下：首先我们需要定义数据结构并借助 map 来统计词频，之后使用小顶堆来保存 K 大元素，注意结果需要按照词频从大到小排列，所以我们需要将出堆元素倒序排列，可以借助链表并采用头插法来实现，题解如下：

    static class WordNum implements Comparable<WordNum> {

        String word;

        int num;

        public WordNum(String word) {
            this.word = word;
            this.num = 1;
        }

        @Override
        public int compareTo(WordNum o) {
            if (this.num != o.num) {
                return this.num - o.num;
            } else {
                return o.word.compareTo(this.word);
            }
        }
    }

    public List<String> topKFrequent(String[] words, int k) {
        HashMap<String, WordNum> map = new HashMap<>();
        for (String word : words) {
            if (map.containsKey(word)) {
                map.get(word).num++;
            } else {
                map.put(word, new WordNum(word));
            }
        }

        PriorityQueue<WordNum> priorityQueue = new PriorityQueue<>();
        for (WordNum value : map.values()) {
            if (priorityQueue.size() < k) {
                priorityQueue.offer(value);
            } else {
                if (value.compareTo(priorityQueue.peek()) > 0) {
                    priorityQueue.poll();
                    priorityQueue.offer(value);
                }
            }
        }

        LinkedList<String> res = new LinkedList<>();
        while (!priorityQueue.isEmpty()) {
            res.addFirst(priorityQueue.poll().word);
        }

        return res;
    }

大顶堆

LCR 159. 库存管理 III 和 面试题 17.14. 最小K个数

这两题都是应用大顶堆求解前K小元素的标准题目，很简单，参考题解如下：

    public int[] inventoryManagement(int[] stock, int cnt) {
        int[] res = new int[cnt];
        if (cnt == 0) {
            return res;
        }
        
        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>((x, y) -> y - x);
        for (int s : stock) {
            if (priorityQueue.size() < cnt) {
                priorityQueue.offer(s);
            } else {
                if (s < priorityQueue.peek()) {
                    priorityQueue.poll();
                    priorityQueue.offer(s);
                }
            }
        }

        for (int i = 0; i < res.length; i++) {
            res[i] = priorityQueue.poll();
        }
        
        return res;
    }

1405. 最长快乐字符串

本题不是 TOP-K 问题，而是使用大顶堆中能获取到其中最大元素的特性来构造字符串。根据题意，需要保证不能有三个相同的字符相同且字符串最长，那么我们可以每次获取到其中数量最大的字符进行拼接，每连续拼接两次则需要获取下一个数量最大的字符再拼接，这样能够保证我们拼接的字符串最长，题解如下：

    static class CharNum implements Comparable<CharNum> {

        char c;

        int num;

        public CharNum(char c, int num) {
            this.c = c;
            this.num = num;
        }

        @Override
        public int compareTo(CharNum o) {
            return o.num - this.num;
        }
    }

    public String longestDiverseString(int a, int b, int c) {
        PriorityQueue<CharNum> charNums = new PriorityQueue<>();
        if (a != 0) {
            charNums.offer(new CharNum('a', a));
        }
        if (b != 0) {
            charNums.offer(new CharNum('b', b));
        }
        if (c != 0) {
            charNums.offer(new CharNum('c', c));
        }

        StringBuilder res = new StringBuilder();
        while (!charNums.isEmpty()) {
            CharNum one = charNums.poll();
            int length = res.length();
            
            if (length >= 2 && res.charAt(length - 1) == one.c && res.charAt(length - 2) == one.c) {
                CharNum two = charNums.poll();
                if (two != null) {
                    res.append(two.c);
                    if (--two.num > 0) {
                        charNums.offer(two);
                    }
                    charNums.offer(one);
                } else {
                    break;
                }
            } else {
                res.append(one.c);
                if (--one.num > 0) {
                    charNums.offer(one);
                }
            }
        }

        return res.toString();
    }

中位数问题

求数据流的中位数问题可以借助两个堆来解决：大顶堆保存数据流中前一半元素，小顶堆保存数据流中后一半元素，如果数据流中元素数量为奇数，那么取大顶堆的堆顶元素为中位数；如果数据流中的元素数为偶数，分别取大顶堆和小顶堆的堆顶元素，求和除以二即为中位数。

295. 数据流的中位数

大家可以拿这道题来练练手，还是比较简单的，题解如下：

class MedianFinder {

    PriorityQueue<Integer> left;

    PriorityQueue<Integer> right;

    public MedianFinder() {
        left = new PriorityQueue<>((x, y) -> y - x);
        right = new PriorityQueue<>();
    }

    public void addNum(int num) {
        if (left.size() == right.size()) {
            right.offer(num);
            left.offer(right.poll());
        } else {
            left.offer(num);
            right.offer(left.poll());
        }
    }

    public double findMedian() {
        return left.size() == right.size() ? (left.peek() + right.peek()) / 2.0 : left.peek();
    }
}

堆

到这里我们基本了解了堆的特性和用法，接下来以小顶堆为例，看下它的实现，我们要弄清楚它是如何保证堆顶元素是最小元素的。

堆的数组实现

使用数组可以高效地实现小顶堆，我们规定索引 0 处的元素不使用，那么堆中所有元素是从索引 1 开始记录的，相应地，若当前节点的索引为 k，那么它的父节点为 k/2（根节点除外），左子节点索引为 2k，右子节点索引为 2k + 1。当堆中每个节点都小于等于它的两个子节点时，我们称它为 堆有序。

由上至下的堆有序化（swim）

如果堆的有序状态因为某个节点变得比它的父节点更小而被打破，那么我们需要通过交换它和它的父节点来修复有序关系，交换完成后，这个节点比它的两个子节点都小，但这个节点仍然可能比它的父节点更小，所以我们需要一遍一遍地（while）修复有序关系，直到遇到更小的父节点或者到达根节点位置。这个方法实现起来比较简单，如下：

    /**
     * 由下至上堆有序化（上浮）
     */
    private void swim(int index) {
        while (index > 1 && nums[index] < nums[index / 2]) {
            swap(index, index / 2);
            index /= 2;
        }
    }

由下至上的堆有序化（sink）

如果堆的有序状态因为某个节点变得比它的两个子节点之一更大而被打破，那么我们需要通过交换它和它的两个子节点中较小的节点来修复有序关系，同样地，我们也需要一遍一遍地（while）来执行这个逻辑，直到它的两个子节点都比它大或者它到达了堆底。该方法的实现如下：

    /**
     * 由上至下堆有序化（下沉）
     */
    private void sink(int index) {
        while (index * 2 <= size) {
            int son = index * 2;
            if (son + 1 <= size && nums[son + 1] < nums[son]) {
                son++;
            }
            if (nums[index] > nums[son]) {
                swap(index, son);
                index = son;
            } else {
                break;
            }
        }
    }

swim() 和 sink() 方法是实现堆的基础 API，有了这两个方法我们能够轻松地实现插入元素和最小元素出堆的操作

插入元素：增加堆的大小并将新元素直接插入到数组末尾，再让这个新元素上浮到合适的位置即可
最小元素出堆：将堆顶元素移除并将堆底元素放到堆顶，减小堆的大小并让这个元素下沉到合适的位置即可

按照以上逻辑，固定大小堆的代码实现如下：

public class MyPriorityQueue {

    int[] nums;

    int size;

    int capacity;

    public MyPriorityQueue(int n) {
        // 不使用 0 索引
        nums = new int[n + 1];
        this.capacity = n;
        this.size = 0;
    }

    public int size() {
        return size;
    }

    /**
     * 获取堆顶元素，即最小值
     */
    public int peek() {
        if (size == 0) {
            return -1;
        }

        return nums[1];
    }

    /**
     * 元素入堆操作，先将该元素赋值在堆底，并不断地和比自己大的父节点交换位置
     */
    public void offer(int num) {
        if (size + 1 <= capacity) {
            nums[++size] = num;
            swim(size);
        }
    }

    /**
     * 由下至上堆有序化（上浮）
     */
    private void swim(int index) {
        while (index > 1 && nums[index] < nums[index / 2]) {
            swap(index, index / 2);
            index /= 2;
        }
    }

    /**
     * 元素出堆操作，将堆顶元素与堆底元素交换位置，并不断地和比自己小的子节点交换位置
     */
    public int poll() {
        if (size == 0) {
            return -1;
        }

        int res = nums[1];
        swap(1, size--);
        sink(1);

        return res;
    }

    /**
     * 由上至下堆有序化（下沉）
     */
    private void sink(int index) {
        while (index * 2 <= size) {
            int son = index * 2;
            if (son + 1 <= size && nums[son + 1] < nums[son]) {
                son++;
            }
            if (nums[index] > nums[son]) {
                swap(index, son);
                index = son;
            } else {
                break;
            }
        }
    }

    private void swap(int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

多路归并

堆能用来解决多路归并问题，它可以将 多个有序的输入流归并成一个有序的输出流，下面是使用堆来解决多路归并问题的样例：

public class Multiway {

    public static void main(String[] args) {
        Multiway multiway = new Multiway();
        multiway.merge(new int[][]{{1, 3, 9}, {2, 4, 8}, {5, 6, 7}});
    }

    public void merge(int[][] streams) {
        int N = streams.length;
        // streamIndex, numIndex, num
        PriorityQueue<int[]> priorityQueue = new PriorityQueue<>(Comparator.comparingInt(x -> x[2]));
        for (int i = 0; i < streams.length; i++) {
            priorityQueue.offer(new int[]{i, 0, streams[i][0]});
        }

        while (!priorityQueue.isEmpty()) {
            int[] min = priorityQueue.poll();
            System.out.println(min[2]);

            if (min[1] + 1 < streams[min[0]].length) {
                priorityQueue.offer(new int[]{min[0], min[1] + 1, streams[min[0]][min[1] + 1]});
            }
        }
    }
}

我来简单解释下多路归并的逻辑：将多个有序输入流中最小元素放入小根堆中，在多路归并过程中每个输入流至多与堆关联一个元素，之后执行出堆操作，每次操作将堆顶元素移除，这保证了每次移除的元素都是当前输入流中最小的元素，每有元素出堆，都要检查该输入流中是否还有元素，有的话则继续插入堆中，没有则证明该输入流已经被遍历完了，再继续处理其他输入流直到堆中没有任何元素即可。

堆排序

我们可以通过大根堆对数组进行排序，重复调用最大元素出堆的操作，并将该元素放在数组的末端，这样的排序我们称它为 堆排序。堆排序可以分成两个阶段，建堆和 下沉排序：

建堆：将原始数组构建成大根堆。在前文我们说过，堆是一棵完全二叉树，记树的节点数量为 n，完全二叉树的叶子节点数量为 n/2 或 n/2 + 1，那么非叶子节点数量为 ⌊n⌋，而每个叶子节点我们都可以看成只包含一个元素的堆，所以这些节点是需要进行建堆操作的，我们只需要对非叶子节点建堆即可
下沉排序：建堆完成后，堆顶为最大元素，我们每次将最大元素排在数组最右端未被占用的位置即可，这个过程和选择排序类似，但是所需的比较次数少得多，因为堆能高效地从未排序部分找到最大元素

堆排序的代码如下：

public class DeapSort {

    public void sort(int[] nums) {
        int n = nums.length - 1;

        // 1. 建堆
        for (int i = n / 2; i > 0; i--) {
            sink(nums, i, n);
        }
        // 2. 下沉排序
        while (n > 1) {
            swap(nums, n, 1);
            sink(nums, 1, --n);
        }
    }

    private void sink(int[] nums, int i, int n) {
        while (i * 2 <= n) {
            int max = i * 2;
            if (max + 1 <= n && nums[max + 1] > nums[max]) {
                max++;
            }
            if (nums[i] < nums[max]) {
                swap(nums, i, max);
                i = max;
            } else {
                break;
            }
        }
    }

    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

算法特性：

时间复杂度：O(nlogn)
空间复杂度：O(1)
原地排序
非稳定排序
非自适应排序

贪心算法

在贪心算法中使用堆是借助堆能获取到当前元素中的最值的特点，我们需要确定 堆中需要放什么元素和它的排序规则，以及 元素进堆和出堆的条件

1705. 吃苹果的最大数目

我们把需要确定的条件列一下：

堆中保存的元素和排序规则：保存的元素是苹果的数量和它的过期时间，并按照过期时间从早到晚排序，优先将过期早的苹果吃掉保证吃掉的苹果数目最多
元素进堆的条件：到了哪天便把哪天成熟的苹果进堆
元素出堆条件：苹果过期或者把苹果吃光了，元素出堆

逻辑不难，题解如下：

    public int eatenApples(int[] apples, int[] days) {
        // applesNum, endDay
        PriorityQueue<int[]> priorityQueue = new PriorityQueue<>(Comparator.comparingInt(x -> x[1]));

        int day = 0;
        int res = 0;
        while (day < apples.length || !priorityQueue.isEmpty()) {
            if (day < apples.length && apples[day] > 0) {
                priorityQueue.offer(new int[]{apples[day], day + days[day]});
            }

            // 过期的都扔掉
            while (!priorityQueue.isEmpty() && day >= priorityQueue.peek()[1]) {
                priorityQueue.poll();
            }
            if (!priorityQueue.isEmpty()) {
                int[] apple = priorityQueue.peek();
                apple[0]--;
                res++;
                if (apple[0] == 0) {
                    priorityQueue.poll();
                }
            }
            day++;
        }

        return res;
    }

1834. 单线程 CPU

本题相对来说困难一些，我们一起来看一下：

堆中保存的元素和排序规则：想要获取最佳的处理任务顺序，那么 CPU 一定优先处理时间短的任务，如果处理时间相同，则优先处理索引小的任务，堆需要按照这个规则对任务进行排序，那么我们其中保存的元素就包括了索引和任务的处理时间信息
元素进堆的条件：当前时间大于任务开始执行的时间
元素出堆条件：任务根据排序规则逐个出堆即可，代表 CPU 逐个执行任务

任务的开始时间影响 CPU 是否能执行该任务，那么我们需要对所有的任务按照开始时间递增的顺序进行排序，从而能获取到第一个能够执行的任务，后续如果优先队列中没有任务可处理时，那么直接让当前时间等于下一个需要处理的任务的开始时间，题解如下：

    static class IndexProcessTime implements Comparable<IndexProcessTime> {

        int index;

        int beginTime;

        int processTime;

        public IndexProcessTime(int index, int beginTime, int processTime) {
            this.index = index;
            this.beginTime = beginTime;
            this.processTime = processTime;
        }

        @Override
        public int compareTo(IndexProcessTime o) {
            return this.beginTime - o.beginTime;
        }
    }

    public int[] getOrder(int[][] tasks) {
        ArrayList<IndexProcessTime> list = new ArrayList<>(tasks.length);
        for (int i = 0; i < tasks.length; i++) {
            list.add(new IndexProcessTime(i, tasks[i][0], tasks[i][1]));
        }
        Collections.sort(list);
        // taskIndex, processTime
        PriorityQueue<IndexProcessTime> priorityQueue = new PriorityQueue<>((x, y) -> {
            if (x.processTime == y.processTime) {
                return x.index - y.index;
            } else {
                return x.processTime - y.processTime;
            }
        });

        int index = 0;
        int[] res = new int[list.size()];
        int beginTime = 0;
        for (int i = 0; i < list.size() || !priorityQueue.isEmpty(); ) {
            while (i < list.size() && beginTime >= list.get(i).beginTime) {
                IndexProcessTime task = list.get(i++);
                priorityQueue.offer(new IndexProcessTime(task.index, task.beginTime, task.processTime));
            }

            if (!priorityQueue.isEmpty()) {
                IndexProcessTime task = priorityQueue.poll();
                res[index++] = task.index;
                // 增加处理时间
                beginTime += task.processTime;
            } else {
                beginTime = list.get(i).beginTime;
            }
        }

        return res;
    }

871. 最低加油次数

本题虽然是困难的题目，但是我觉得是这三道题里最简单的了，本题的解题思路可以用一句话来概括：记录车能跑的最远距离，并把经过的加油站按照油量加入大顶堆，每次油不够的时候就拿油最多的加上，这样能保证加油的次数最少，最终如果油加完了还不够则返回 -1，否则为最少加油次数，不过我们还是要把需要关注的点说明下：

堆中保存的元素和排序规则：保存的元素是加油站油量，油量最多的在堆顶
元素进堆的条件：车行驶的距离超过加油站的距离，则加油站油量进堆
元素出堆条件：车行驶距离不够到达目的地，油量最多的出堆，给车加油

    public int minRefuelStops(int target, int startFuel, int[][] stations) {
        Arrays.sort(stations, Comparator.comparingInt(x -> x[0]));
        // 保存油量
        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>((x, y) -> y - x);

        int index = 0;
        int res = 0;
        while (startFuel < target) {
            while (index < stations.length && startFuel >= stations[index][0]) {
                priorityQueue.offer(stations[index++][1]);
            }
            if (priorityQueue.isEmpty()) {
                return -1;
            } else {
                startFuel += priorityQueue.poll();
                res++;
            }
        }

        return res;
    }