二维空间与三维空间的姿态表示法
- 一、2D空间姿态表示法
- 二、3D空间姿态表示法
- 2.1 三个数表示空间姿态
- 问题
- 2.2 九个数表示空间姿态
- 问题
- 2.3 四个数表示空间姿态
- 结语
- Reference
假设,你有志成为我空军某航空旅歼-20飞行员,但要想开好飞机,那就得锻炼身体,好好学习,因此,你刻苦学习专业知识,并梦想有一天,能真正演练编队飞行技术和空中作战战术,下面,未来的飞行员同志,在此之前,你需要学习以下内容。首先注意,这里是 姿态表示法,而不是 位置表示法,平面位置表示法有二维笛卡尔坐标系,空间位置表示法有三维笛卡尔坐标系,这个很容易理解。
一、2D空间姿态表示法
看完这篇《旋转与复数》,就知道为什么复数相乘,能表示平面向量的旋转了,总结:
z
1
=
a
1
+
b
1
i
=
r
1
c
o
s
θ
1
+
i
r
1
s
i
n
θ
1
=
r
1
(
c
o
s
θ
1
+
i
s
i
n
θ
1
)
=
r
1
e
i
θ
1
z_1 = a_1+b_1i \\ =r_1cos\theta_1 + ir_1sin\theta_1 \\ =r_1(cos\theta_1 + isin\theta_1) \\ = r_1e^{i\theta_1}
z1=a1+b1i=r1cosθ1+ir1sinθ1=r1(cosθ1+isinθ1)=r1eiθ1
z
2
=
a
2
+
b
2
i
=
r
2
c
o
s
θ
2
+
i
r
2
s
i
n
θ
2
=
r
2
(
c
o
s
θ
2
+
i
s
i
n
θ
2
)
=
r
2
e
i
θ
2
z_2 = a_2+b_2i \\ =r_2cos\theta_2 + ir_2sin\theta_2 \\ =r_2(cos\theta_2 + isin\theta_2) \\ = r_2e^{i\theta_2}
z2=a2+b2i=r2cosθ2+ir2sinθ2=r2(cosθ2+isinθ2)=r2eiθ2
有
z
1
∗
z
2
=
r
1
r
2
e
i
(
θ
1
+
θ
2
)
z_1*z_2 = r_1r_2e^{i(\theta1+\theta_2)}
z1∗z2=r1r2ei(θ1+θ2)
所以,两个复平面的向量相乘,代表的含义是:长度相乘,角度相加,即“长乘角加”,这里的角度是有正负的。根据上述公式可以看出:
若
z
2
z_2
z2向量的
r
2
=
1
r_2=1
r2=1,也就是说
z
2
z_2
z2是一个单位长度的向量,就只有角度相加
若
z
2
z_2
z2向量的
θ
2
=
θ
1
\theta_2=\theta_1
θ2=θ1,也就是说
z
2
z_2
z2向量的方向和
z
1
z_1
z1一样,就只有长度相乘
所以复平面具备美妙的构造,有着非常美妙的性质,以后看到复平面的向量计算,就会更加直观了,但你并不满足只在平面国成为一名飞行员,你想在三维的世界翱翔,有了这个基础,可以开始挑战高难度。
以前对构造和性质这两个词理解不深刻,后面发现实际应用中,很多数学公式就是为了满足某种性质而特意构造出来的,俗称先射箭再画靶,比如损失函数,完全没有推理可言,损失函数不是推导出来的,就是为了满足某种性质从构造出来的。
二、3D空间姿态表示法
2.1 三个数表示空间姿态
这是最自然的方式,一开始我也是这么想的,我想你一开始也会这么想,令人欣慰的是,大数学家欧拉也是这么想滴。欧拉角总共有三个角,其英文分别是pitch,yaw,roll,翻译为俯仰角,偏航角,翻滚角,动画效果展示请看《欧拉角pitch、yaw,roll的理解》,有了这个理解,就可以开始了。
问题
这种表示法真的没问题吗?有,欧拉角表示法存在万向死锁的问题,实在不理解,上淘宝搜索,太空环玩具,玩一玩就理解了。
拿下面这张图举例,就会出现死锁,保持绿色环相对位置不动,转动黄色环和转动粉色环,效果都是俯仰。归位,保持黄色和粉色环和不动,转动绿色环,效果是偏航。“莫名其妙”地少了一个方向的旋转!!!

【无伤理解欧拉角中的“万向死锁”现象 - bilibili】
2.2 九个数表示空间姿态
这九个数组成了一个矩阵, X ^ B \hat{X}_{B} X^B表示物体B在其自身坐标系X方向的主轴向量,第一列该向量在世界坐标系上三个方向上的投影,这里的世界坐标系就是指A所处的坐标系。
[
X
^
B
⋅
X
^
A
Y
^
B
⋅
X
^
A
Z
^
B
⋅
X
^
A
X
^
B
⋅
Y
^
A
Y
^
B
⋅
Y
^
A
Z
^
B
⋅
Y
^
A
X
^
B
⋅
Z
^
A
Y
^
B
⋅
Z
^
A
Z
^
B
⋅
Z
^
A
]
\begin{bmatrix} \hat{X}_{B}·\hat{X}_{A} & \hat{Y}_{B}·\hat{X}_{A} & \hat{Z}_{B}·\hat{X}_{A} \\ \hat{X}_{B}·\hat{Y}_{A} & \hat{Y}_{B}·\hat{Y}_{A} & \hat{Z}_{B}·\hat{Y}_{A} \\ \hat{X}_{B}·\hat{Z}_{A} & \hat{Y}_{B}·\hat{Z}_{A} & \hat{Z}_{B}·\hat{Z}_{A} \end{bmatrix}
X^B⋅X^AX^B⋅Y^AX^B⋅Z^AY^B⋅X^AY^B⋅Y^AY^B⋅Z^AZ^B⋅X^AZ^B⋅Y^AZ^B⋅Z^A
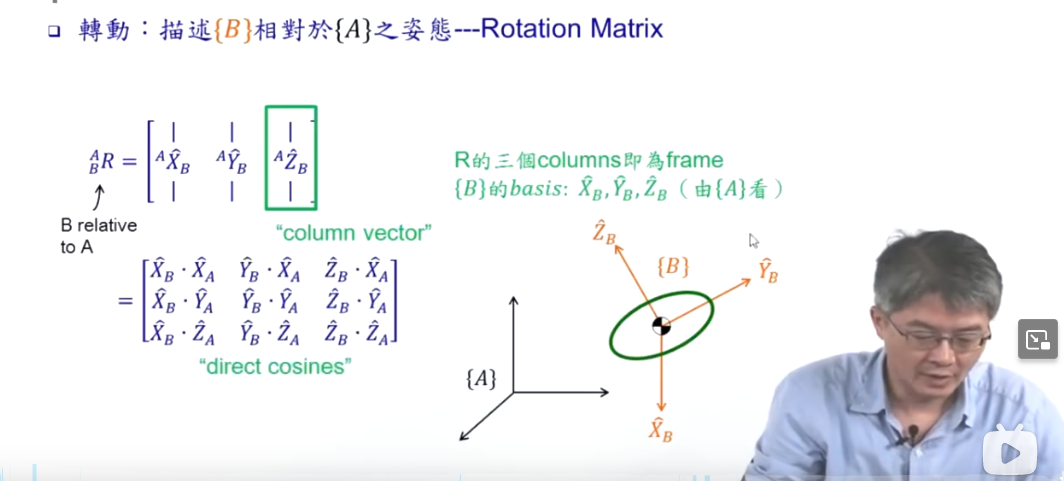
【【机械臂运动学教程】机械臂+旋转矩阵+变换矩阵+DH+逆解+轨迹规划+机器人+教程】—— 台湾大学
问题
但这种方式也是有问题的,会有误差累计问题
2.3 四个数表示空间姿态
3Blue1Brown是最受欢迎的数学区科普UP,可以按顺序观看他发的这两个视频:【四元数的可视化 - bilibili】,【四元数和三维转动,可互动的探索式视频(请看链接)】,但后面的视频并没说为什么要右乘逆矩阵,可以看评论区用户冰月旋律的留言:“ q ∗ p ∗ q − 1 q * p * q^{-1} q∗p∗q−1 得到什么? 2次同样的旋转与1轮抵消的缩放”,及此问答 Why does rotation by a quaternion require multiplying two times?,稍后会证明并解释。
总结如下:
(1) 四元数计算规则
规则记忆方式,
i
→
j
→
k
→
i
→
j
.
.
.
.
.
.
i \rightarrow j \rightarrow k \rightarrow i \rightarrow j ......
i→j→k→i→j......,两两一组计算得到下一个,若顺序相反,就要带负号。

 这里
v
1
→
∗
v
2
→
v^\rightarrow_1 * v^\rightarrow_2
v1→∗v2→是叉乘(外积)
这里
v
1
→
∗
v
2
→
v^\rightarrow_1 * v^\rightarrow_2
v1→∗v2→是叉乘(外积)
(2)
q
⋅
p
q·p
q⋅p,前面的
q
q
q 视作一个作用于点
p
p
p 的
f
u
n
c
t
i
o
n
function
function ,代表对
p
p
p进行拉伸与旋转。
(3) 1D-3D球极投影截图:
 (4)对实部为0的一个虚四元数
p
p
p ,进行旋转,需要左乘
q
q
q 和右乘
q
−
1
q^{-1}
q−1,即
p
′
=
q
p
q
−
1
p^{'} = qpq^{-1}
p′=qpq−1 才是一个完整的旋转操作。
(4)对实部为0的一个虚四元数
p
p
p ,进行旋转,需要左乘
q
q
q 和右乘
q
−
1
q^{-1}
q−1,即
p
′
=
q
p
q
−
1
p^{'} = qpq^{-1}
p′=qpq−1 才是一个完整的旋转操作。
下面是证明,首先复习共轭复数(conjugate complex number),
a
+
b
i
a+bi
a+bi 与
a
−
b
i
a-bi
a−bi 是一对共轭复数,它们实部相同,虚部相反,四元数与之类似,有四元数
q
q
q:
q
=
w
+
x
i
+
y
j
+
z
k
q = w + x\bold{i} + y\bold{j} + z\bold{k}
q=w+xi+yj+zk
对应的共轭复数为
q
∗
=
w
−
x
i
−
y
j
−
z
k
q^* = w - x\bold{i} - y\bold{j} - z\bold{k}
q∗=w−xi−yj−zk
易得
q
q
∗
=
q
∗
q
=
(
w
2
−
w
x
i
−
w
y
j
−
w
z
k
)
+
(
w
x
i
+
x
2
−
x
y
k
+
x
z
j
)
+
(
w
y
j
+
x
y
k
+
y
2
−
y
z
i
)
+
(
w
z
k
−
x
z
j
+
y
z
i
+
z
2
)
=
w
2
+
x
2
+
y
2
+
z
2
qq^* = q^*q \\ = (w^2 - wx\bold{i} - wy\bold{j} - wz\bold{k}) \\ +(wx\bold{i} + x^2 - xy\bold{k} + xz\bold{j}) \\ +(wy\bold{j} + xy\bold{k} + y^2 - yz\bold{i}) \\ +(wz\bold{k} - xz\bold{j} + yz\bold{i} + z ^2) \\ = w^2 + x^2 + y^2 + z^2
qq∗=q∗q=(w2−wxi−wyj−wzk)+(wxi+x2−xyk+xzj)+(wyj+xyk+y2−yzi)+(wzk−xzj+yzi+z2)=w2+x2+y2+z2
用矩阵的观点来看计算会更快,对结果中的所有元素求和,得到的依旧是
w
2
+
x
2
+
y
2
+
z
2
w^2 + x^2 + y^2 + z^2
w2+x2+y2+z2
[
w
x
i
y
j
z
k
]
[
w
,
−
x
i
,
−
y
j
,
−
z
k
]
=
[
w
2
,
−
w
x
i
,
−
w
y
j
,
−
w
z
k
w
x
i
,
x
2
,
−
x
y
k
,
x
z
j
w
y
j
,
x
y
k
,
y
2
,
−
y
z
i
w
z
k
,
−
x
z
j
,
y
z
i
,
z
2
]
\begin{bmatrix} w \\ xi \\ yj \\ zk \end{bmatrix} \begin{bmatrix} w, -xi, -yj, -zk \end{bmatrix} = \begin{bmatrix} w^2, -wx\bold{i}, - wy\bold{j}, - wz\bold{k} \\ wx\bold{i}, x^2, - xy\bold{k}, xz\bold{j} \\ wy\bold{j}, xy\bold{k}, y^2, - yz\bold{i} \\ wz\bold{k}, - xz\bold{j}, yz\bold{i}, z ^2 \end{bmatrix}
wxiyjzk
[w,−xi,−yj,−zk]=
w2,−wxi,−wyj,−wzkwxi,x2,−xyk,xzjwyj,xyk,y2,−yziwzk,−xzj,yzi,z2
模长为
∣
∣
q
∣
∣
=
w
2
+
x
2
+
y
2
+
z
2
||q|| = \sqrt{w^2 + x^2 + y^2 + z^2}
∣∣q∣∣=w2+x2+y2+z2
且有
∣
∣
q
1
q
2
∣
∣
=
∣
∣
q
1
∣
∣
⋅
∣
∣
q
2
∣
∣
||q_1q_2|| = ||q_1||·||q_2||
∣∣q1q2∣∣=∣∣q1∣∣⋅∣∣q2∣∣
在矩阵中,一个矩阵的逆矩阵,定义为可以得到单位矩阵的行(列)变换矩阵
而四元数中,一个四元数的逆,定义为一个可以通过四元数乘法得到1+0i+0j+0k的四元数
也就是说
q
−
1
=
q
∗
∣
∣
q
∣
∣
2
q
⋅
q
−
1
=
q
−
1
⋅
q
=
1
q^{-1} = \frac{q^*}{||q||^2} \\ q·q^{-1} = q^{-1}·q = \bold{1}
q−1=∣∣q∣∣2q∗q⋅q−1=q−1⋅q=1
现在开始解释,为什么要左乘
p
p
p 和右乘
p
−
1
p^{-1}
p−1 ,首先,我们只想旋转方向,而不想伸缩长度,根据上面的公式
∣
∣
q
p
q
−
1
∣
∣
=
∣
∣
q
p
∣
∣
⋅
∣
∣
q
−
1
∣
∣
=
∣
∣
q
∣
∣
⋅
∣
∣
p
∣
∣
⋅
∣
∣
q
∗
∣
∣
∣
∣
q
∣
∣
2
=
∣
∣
p
∣
∣
||qpq^{-1}|| \\ =||qp|| · ||q^{-1}||\\ =\frac{||q|| · ||p|| · ||q^*||}{||q||^2} \\ =||p||
∣∣qpq−1∣∣=∣∣qp∣∣⋅∣∣q−1∣∣=∣∣q∣∣2∣∣q∣∣⋅∣∣p∣∣⋅∣∣q∗∣∣=∣∣p∣∣
那么确认一点,这样变换不会影响旋转后的点
p
′
p^{'}
p′的模长,接下来要验证,
p
′
p^{'}
p′的实部依旧为0,还是一个虚四元数,这其实都不用验证了,
p
p
p的实部为0,0乘任何数都会为0。然后要验证的是,
q
p
qp
qp与
p
q
−
1
pq^{-1}
pq−1旋转的方向是相同的,其实这个也容易验证,根据之前的记忆法则
i
→
j
→
k
→
i
→
j
i \rightarrow j \rightarrow k \rightarrow i \rightarrow j
i→j→k→i→j,
p
q
−
1
pq^{-1}
pq−1相当于箭头从左到右的运算变成了从右到左,这样会给结果带来负号,但是
q
−
1
=
q
∗
∣
∣
q
∣
∣
2
q^{-1} = \frac{q^*}{||q||^2}
q−1=∣∣q∣∣2q∗,且
q
∗
=
w
−
x
i
−
y
j
−
z
k
q^* = w - x\bold{i} - y\bold{j} - z\bold{k}
q∗=w−xi−yj−zk的虚部都是负数,相当于给带上负号的结果进行了负负得正,因此
q
p
−
1
qp^{-1}
qp−1旋转的方向与
q
p
qp
qp是相同的,这也就解释了为什么会有半角出现,转两次半角等于旋转角度完全到位,证毕。
看这个视频的时候,我感觉,三维复数已经足够表示旋转了,但作者说三维复数实际上无法定义一个有效的计算规则,这个我就不清楚了,视频还说,是哈密顿(Hamiton)发明的vector这个说法,vector之前在数学和物理中从未出现过,用来称呼只有ijk分量而没有标量部分的四元数,查阅Wiki百科发现,哈密顿还有其它贡献
He coined the neologisms “tensor” and “scalar”, and was the first to use the word “vector” in the modern sense. 他创造了“张量”和“标量”这两个新词,并且是第一个使用现代意义上的“向量”一词的人 —— William Rowan Hamilton - Wiki
我还记得我在高中数学课本上看到过四元数的内容,于是去找了找教材,只翻到了在新人教B版数学必修第四册的目录里有,内容就没找到了,所以高中数学教科书的编者早早的跑在前头等着,更令人破防的是,高中数学教科书的很多选修部分,其实涵盖了很多多大学内容,这令我感到一阵脸红,我的水平只有高中?谁道人生无再少,门前流水尚能西,修将白发唱黄鸡。《中小学电子版教材,看这12个网站就够了》- 进击的金牛的文章 - 知乎
结语
《上海交通大学学生生存手册》里有两句话,我深以为然:“我无意全盘否定同学们吃苦耐劳的精神,但这份精神充其量只能称为悲壮。我们耗费了大量的时间和精力掌握的那些考点、技巧,在真正的知识殿堂根本登不上大雅之堂。哪怕我们特征值求的再熟练,积分积得再复杂,中国的载人飞船也不会因此而顺利上天”,“学习最需要的,不是悲壮的毅力,而是对无限未知的渴求”。塔台期盼你早日单飞,平安归来。
Reference
[1] 视觉SLAM十四讲:从理论到实践(第2版)