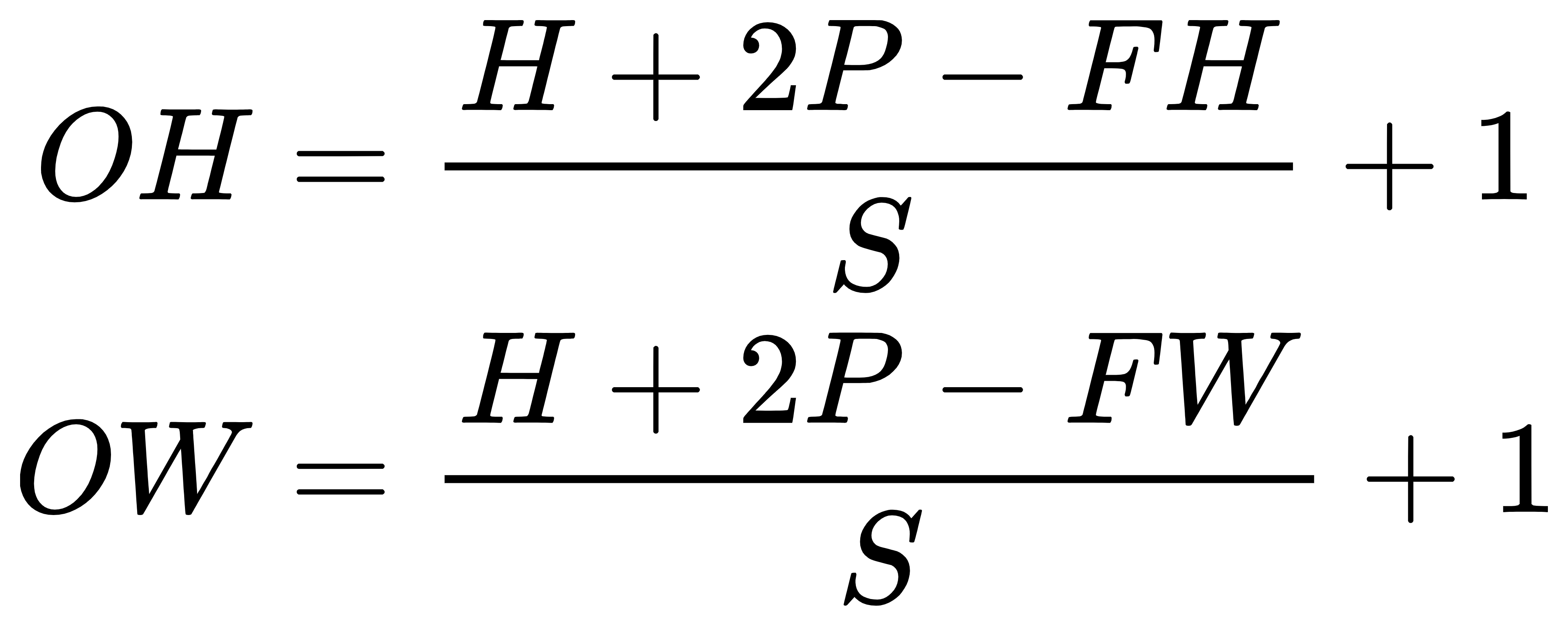DL Homework 6

一、概念

（1）卷积

（2）卷积核

（3）特征图

（4）特征选择

（5）步长

（6）填充

（7）感受野

二、探究不同卷积核的作用

1~3 三种情况下，运用不同的卷积核的代码分析

4. 实现灰度图的边缘检测、锐化、模糊

5. 总结不同卷积核的特征和作用

总结

参考文献

本博客引用了几个比较著名的DL的书这里介绍一下

DL-深度学习入门（斋藤康毅）—— 鱼书邱老师著的

DL-动手学深度学习—— 沐神写的，关于实操真的很给力的一本书

一、概念

（1）卷积

首先，从沐神对数学定义上的卷积定义开始，定义如下:

在数学中，两个函数（⽐如 $f, g : \mathbb{R}^d\rightarrow \mathbb{R}$ ）之间的“卷积”被定义为

$(f*g)(x) = \int f(z)g(x-z)dz$

也就是说，卷积是当把⼀个函数“翻转”并移位x时，测量f和g之间的重叠。当为离散对象时，积分就变成求和。这才是卷积的原理，不理解没关系，不影响咱们的理解。

图像卷积，也就是我们日常所说的卷积，严格来说，沐神明确指出卷积层是个错误叫法，因为他所表达的运算其实是互相关运算而不是卷积运算。

鱼书就同沐神的想法一样中把卷积理解为一种运算，将各个位置上滤波器的元素和输入的对应元素相乘，然后再求和（有时将这个计算称为乘积累加运算）。然后，将这个结果保存到输出的对应位置。将这个过程在所有位置都进行一遍，就可以得到卷积运算的输出。过程如下图所示

综上所述，卷积就是一种卷积神经网络特有的，基于数学卷积的原理，不同于互相关运算的新运算方式——旨在采用不同的滤波器提取信号序列中的不同特征。

（2）卷积核

又叫做滤波器，卷积核是一个小矩阵，通常大小为 $K*K$ ，通常小于需要被卷积的矩阵。其中 $K$ 是一个奇数。卷积核内的每个元素都是一个实数或一个权重，用于与输入图像的对应像素进行乘法运算并求和。

搜到这个定义的时候我就很疑惑为什么定义中的K一定是奇数呢？

1、在二维卷积操作中，卷积核通常被放置在输入图像的中心位置，然后进行点乘并相加。如果卷积核大小 $K$ 是偶数，那么在将卷积核放置在中心位置时，就会存在两个中心像素，无法确定使用哪个像素作为计算中心。这将导致输出结果不稳定，难以正确解释。

2、卷积核大小 $K$ 为奇数时，它可以具有对称性和可逆性，因为 $K$ 是奇数，所以卷积核可以完全对称，即中心元素周围的元素数量相等。这使得卷积操作更加有效和稳定，可以更好地捕获输入图像中的特征。

滤波器没什么好解释的，卷积运算使用的移动的矩阵就是卷积核，并且在这里提一嘴，上面刚说完卷积不同于互相关运算，但为什么还总可以把互相关运算叫做卷积运算呢，因为互相关运算和卷积的区别仅仅在于卷积核是否进行翻转,因此互相关被称为不反转卷积，并且互相关运无论执行的是卷积运算还是互相关运算，卷积的结果都不会受到影响，因为卷积核是从数据中学习来的，再详细点说:神经网络使用卷积就是为了进行特征抽取，但是卷积核无论是否进行反转和其特征抽取的能力无关，特别是当卷积核是可学习参数时，卷积和互相关在能力上是等价的。所以为了实现和描述的方便我们都采用互相关操作代替卷积操作，但依旧称这个过程叫为卷积。

（3）特征图

在卷积神经网络中，特征图（Feature Map）是指卷积层的输出。当输入数据通过卷积层时，卷积核会对输入数据进行卷积操作，生成一个新的输出图像，也称为特征映射或特征图。特征图可以被看作是对原始输入数据的一种高级表示，其中每个像素值都代表了输入数据中某种特征的强度或存在程度。

为什么要引入特征图的概念呢，有什么好处?

沐神在书中明确指出由于卷积神经网络具有平移不变性和空间局部性等特性，特征图可以有效地捕获输入数据中的局部特征，以前，多层感知机可能需要数⼗亿个参数来表⽰⽹络中的⼀层，⽽现在卷积神经⽹络通常只需要⼏百个参数，⽽且不需要改变输⼊或隐藏表⽰的维数并且在不同位置都能够识别相同的模式。大大提升了效率和准确率。

如（1）卷积的图中输出的卷积层有时被称为特征映射（feature map），因为它可以被视为⼀个输入映射到下⼀层的空间维度的转换器。

（4）特征选择

特征选择（Feature Selection）是指通过卷积操作来从输入数据中提取最重要、最具代表性的特征。

特征选择的过程是在卷积操作中自动进行的。通过学习卷积核的权重参数，网络可以自动选择对于当前任务最有用的特征。在训练过程中，网络会根据损失函数的反向传播，调整卷积核的权重，使得网络能够更好地分类或回归。

特征选择是卷积神经网络的关键步骤之一，它能够帮助网络从原始输入数据中提取出最关键的特征，减少冗余信息，并提高网络的性能和泛化能力。通过自动学习和选择特征，卷积神经网络能够在各种任务中实现优秀的性能，如图像分类、目标检测、语音识别等。

特征选择是指卷积神经网络通过学习和调整卷积核的权重参数，从输入数据中提取最有用的特征。

（5）步长

邱老师和沐神又把步长叫为步幅，在邱老师鱼书中是这样定义的应用滤波器的位置间隔称为步幅（stride）。在沐神的书中是这样定义的每次滑动元素的数量称为步幅（stride）。

邱老师的例子：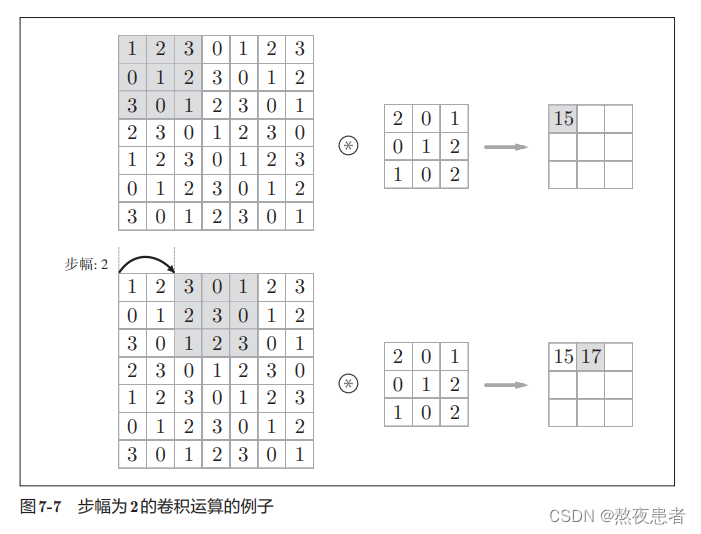

沐神的例子:

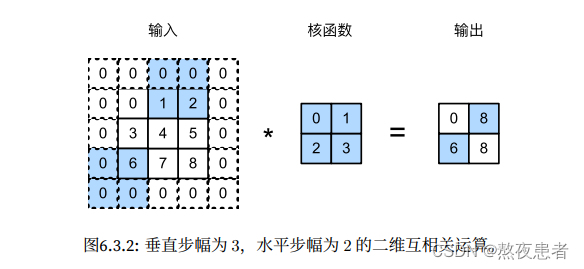
沐神的例子需要简单解释一下，如图是垂直步幅为3，⽔平步幅为2的⼆维互相关运算，为了计算输出中第⼀列的第⼆个元素和第⼀⾏的第⼆个元素，卷积窗⼝分别向下滑动三⾏和向右滑动两列。但是，当卷积窗⼝继续向右滑动两列时，没有输出，因为输⼊元素⽆法填充窗⼝。

两位大咖讲的比较明白，因为这个也比较好理解，就是卷积核移动元素数量，这里就不多加解释了

（6）填充

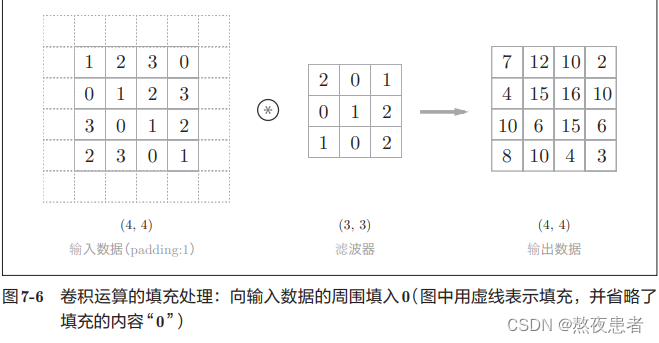
邱老师是这样定义的：在进行卷积层的处理之前，有时要向输入数据的周围填入固定的数据（比如0等），这称为填充（padding）.沐神是这样说的:在输⼊图像的边界填充元素（通常填充元素是0）

邱老师的实例如下，很好理解，因为沐神和邱老师的差不多，没有新的内容，这里就不展示了。

为什么要用填充呢？

沐神在书中是这样说的在应⽤多层卷积时，我们常常丢失边缘像素。由于我们通常使⽤⼩卷积核，因此对于任何单个卷积，我们可能只会丢失⼏个像素。但随着我们应⽤许多连续卷积层，累积丢失的像素数就多了。解决这个问题的简单⽅法即为填充（padding）

那究竟何为填充，我来概括一下，填充是指在输入数据的周围填充一定数量的虚拟像素，以便于在卷积运算中保留输入数据的空间信息，减少特征图大小的下降，从而避免信息的丢失。

这里再扩展一下，输出图像的大小怎么求？

引用邱老师的推导，假设输入大小为(H, W)，滤波器大小为(FH, FW)，输出大小为 (OH, OW)，填充为P，步幅为S。此时，输出大小为

（7）感受野

沐神在书中对感受野的定义是这样的在卷积神经⽹络中，对于某⼀层的任意元素x，其感受野（receptive field）是指在前向传播期间可能影响x计算的所有元素（来⾃所有先前层）。

大佬的书都没有给感受野的图示，于是我上网搜索的过程中看到一个较明确的，展示如下：

第一层感受野:

第二次感受野：

第三层感受野：

详细链接如下，讲的真的还不戳：

阅读笔记4——感受野-CSDN博客https://blog.csdn.net/python_plus/article/details/129077922?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522169912915416800182769842%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=169912915416800182769842&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduend~default-1-129077922-null-null.142%5Ev96%5Epc_search_result_base2&utm_term=%E6%84%9F%E5%8F%97%E9%87%8E%E7%A4%BA%E6%84%8F%E5%9B%BE&spm=1018.2226.3001.4187

当使用卷积遍历某个图片时，感受野过大或过小都是不合适的。

若目标相对感受野过小，那训练参数只有少部分是对应于训练目标的，则在测试环节，也很难检测出类似的目标；
若目标相对感受野过大，那训练的参数都是对应于整个对象的局部信息，是不够利于检测大小目标的。

所以对于感受野的大小选择，还是应当适当选取。

我感觉这个定义太草率，通过大量资料我发现在卷积神经网络中，感受野是指卷积层中每个输出特征图中的像素，在输入数据中所对应的区域大小。通过搜索到的资料我发现，感受野的大小与卷积层数、卷积核大小、步长以及填充等超参数有关。在卷积操作中，每个卷积核会对应一个感受野，在进行卷积操作时，它只会考虑输入数据中与感受野重叠的部分，并将其作为输入数据的一部分。因此，随着网络深度的增加，感受野也会逐渐扩大，从而使网络能够捕获更大范围的空间信息。并且，我发现感受野的大小可以用来评估网络的感知力和能力，较大的感受野可以帮助网络理解更大范围的输入数据，从而提高分类或回归的准确性。同时，大感受野的网络可能会增加训练时间和计算成本，因此需要进行权衡。

二、探究不同卷积核的作用

1. 图1使用卷积核 $gif.latex?%5Cbegin%7Bpmatrix%7D%201%20%26%20-1%20%5Cend%7Bpmatrix%7D$ 和 $gif.latex?%5Cbegin%7Bpmatrix%7D%201%5C%5C%20-1%5C%5C%20%5Cend%7Bpmatrix%7D$ ，输出特征图

import numpy as np
import torch
import matplotlib.pyplot as plt


plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

# 卷积层的权重参数通常具有四个维度：[输出通道数, 输入通道数, 卷积核高度, 卷积核宽度]。因此，在使用conv1进行卷积操作之前，需要确保输入的权重参数weight满足这个维度要求。
w1 = np.array([1, -1], dtype='float32').reshape([1, 1, 1, 2])
w2 = np.array([1, -1], dtype='float32').T.reshape([1, 1, 2, 1])
w1 = torch.Tensor(w1)
w2 = torch.Tensor(w2)
conv1 = torch.nn.Conv2d(1, 1, (1, 2))
conv1.weight = torch.nn.Parameter(w1)
conv2 = torch.nn.Conv2d(1, 1, (2, 1))
conv2.weight = torch.nn.Parameter(w2)

# 创建图像
img = np.ones([7, 6], dtype='float32')
img[:, 3:] = 0.
img[:, :3] = 255.
x = img.reshape([1, 1, 7, 6])
x = torch.Tensor(x)

y1 = conv1(x).detach().numpy()
y2 = conv2(x).detach().numpy()
plt.subplot(131).set_title('图1')
plt.imshow(img, cmap='gray')
plt.subplot(132).set_title('图1使用卷积核为(1,-1)结果')
plt.imshow(y1.squeeze(), cmap='gray')
plt.subplot(133).set_title('图1使用卷积核为(1,-1)T结果')
plt.imshow(y2.squeeze(), cmap='gray')
plt.show()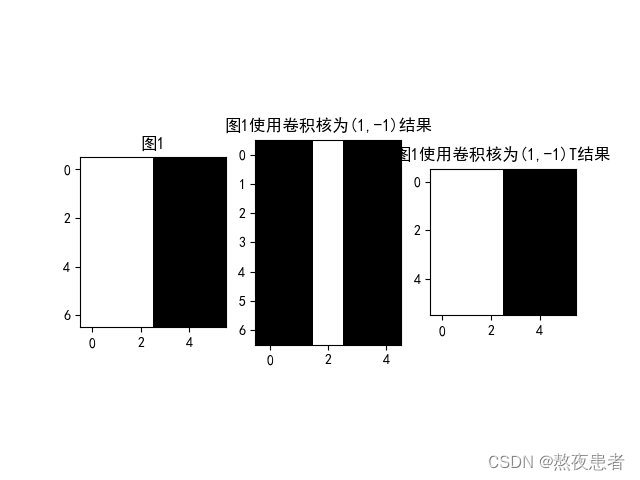

2. 图2分别使用卷积核 $\begin{pmatrix} 1 & -1 \end{pmatrix}$ ， $\begin{pmatrix} 1\\ -1\\ \end{pmatrix}$ 输出特征图

import numpy as np
import torch
import matplotlib.pyplot as plt


plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

# 卷积层的权重参数通常具有四个维度：[输出通道数, 输入通道数, 卷积核高度, 卷积核宽度]。因此，在使用conv1进行卷积操作之前，需要确保输入的权重参数weight满足这个维度要求。
w1 = np.array([1, -1], dtype='float32').reshape([1, 1, 1, 2])
w2 = np.array([1, -1], dtype='float32').T.reshape([1, 1, 2, 1])
w1 = torch.Tensor(w1)
w2 = torch.Tensor(w2)
conv1 = torch.nn.Conv2d(1, 1, (1, 2))
conv1.weight = torch.nn.Parameter(w1)
conv2 = torch.nn.Conv2d(1, 1, (2, 1))
conv2.weight = torch.nn.Parameter(w2)

# 创建图像
img = np.ones([8, 8], dtype='float32')
img[:4, :4] = 0.
img[:4, 4:] = 255.
img[4:, :4] = 255.
img[4:, 4:] = 0.

x = img.reshape([1, 1, 8, 8])
x = torch.Tensor(x)

y1 = conv1(x).detach().numpy()
y2 = conv2(x).detach().numpy()
plt.subplot(131).set_title('图1')
plt.imshow(img, cmap='gray')
plt.subplot(132).set_title('图1使用卷积核为(1,-1)结果')
plt.imshow(y1.squeeze(), cmap='gray')
plt.subplot(133).set_title('图1使用卷积核为(1,-1)T结果')
plt.imshow(y2.squeeze(), cmap='gray')
plt.show()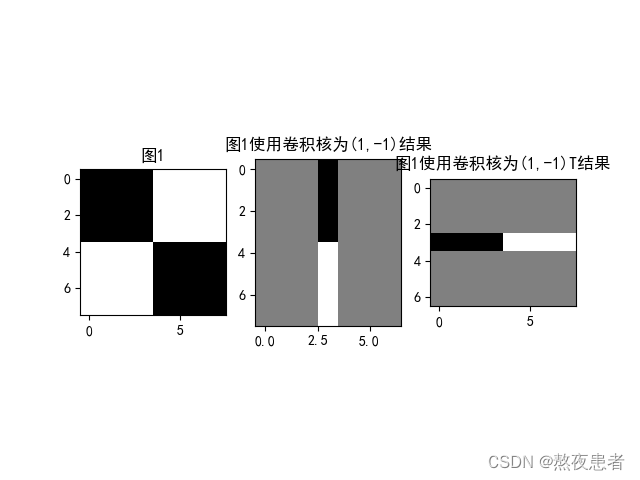

3. 图3分别使用卷积核 $\begin{pmatrix} 1 & -1 \end{pmatrix}$ ， $\begin{pmatrix} 1\\ -1\\ \end{pmatrix}$ ， $\begin{pmatrix} 1 &-1 \\ -1&1 \end{pmatrix}$ ，输出特征图

import numpy as np
import torch
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

w1 = np.array([1, -1], dtype='float32').reshape([1, 1, 1, 2])
w2 = np.array([1, -1], dtype='float32').T.reshape([1, 1, 2, 1])
w3 = np.array([[1, -1, -1, 1]], dtype='float32').reshape([1, 1, 2, 2])
w1 = torch.Tensor(w1)
w2 = torch.Tensor(w2)
w3 = torch.Tensor(w3)
conv1 = torch.nn.Conv2d(1, 1, (1, 2))
conv2 = torch.nn.Conv2d(1, 1, (2, 1))
conv3 = torch.nn.Conv2d(1, 1, (2, 2))
conv1.weight = torch.nn.Parameter(w1)
conv2.weight = torch.nn.Parameter(w2)
conv3.weight = torch.nn.Parameter(w3)

# 创建图像
img = np.ones([9, 9], dtype='float32')
for i in range(7):
    img[i + 1, i + 1] = 255.
    img[i + 1, 7 - i] = 255.

x = img.reshape([1, 1, 9, 9])
x = torch.Tensor(x)

y1 = conv1(x).detach().numpy()
y2 = conv2(x).detach().numpy()
y3 = conv3(x).detach().numpy()
plt.subplot(221).set_title('图3')
plt.imshow(img, cmap='gray')
plt.subplot(222).set_title('图3使用卷积核为(1,-1)结果')
plt.imshow(y1.squeeze(), cmap='gray')
plt.subplot(223).set_title('图3使用卷积核为(1,-1)T结果')
plt.imshow(y2.squeeze(), cmap='gray')
plt.subplot(224).set_title('图3使用卷积核为[[1 -1],[-1 1]]结果')
plt.imshow(y3.squeeze(), cmap='gray')
plt.show()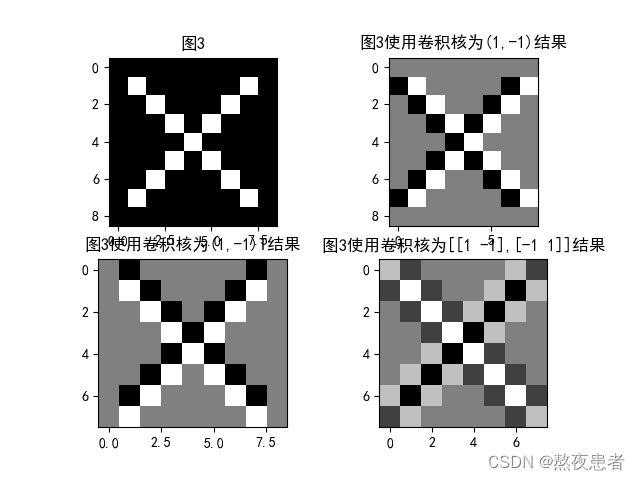

1~3 三种情况下，运用不同的卷积核的代码分析

下面是对代码中出现的函数的简单介绍

1、torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride, padding, bias) #2维卷积层
in_channels(int) – 输入信号的通道
out_channels(int) – 卷积产生的通道
kerner_size(int or tuple) - 卷积核的尺寸
stride(int or tuple, optional) - 卷积步长
padding (int or tuple, optional)- 输入的每一条边补充0的层数
dilation(int or tuple, `optional``) – 卷积核元素之间的间距
groups(int, optional) – 从输入通道到输出通道的阻塞连接数
bias(bool, optional) - 如果bias=True，添加偏置

2、为什么利用torch.nn.Parameter需要四维数据，都是哪四维？

四维数据为 (N,C_in,H,W)|(N,C_out,H,W)

N——batch_size:一次训练所抓取的数据样本数量

C_in/C_out——输入图像的通道数:RGB\BGR图像这一维度就是3

H，W——对应的就是输入图像的高和宽

3、conv1(x).detach().numpy()什么含义

.detach() 是一个函数，用于将输出结果从计算图中分离出来，即断开梯度的传播。这样做可以防止在模型的反向传播过程中对该输出结果进行梯度更新。

.numpy() 是一个方法，用于将张量（Tensor）对象转换为NumPy数组。这意味着将 conv1(x) 的输出结果转换为NumPy数组。

将输入数据 x 通过卷积层 conv1 进行卷积操作，并将卷积层的输出结果转换为NumPy数组。

4、中文画图、正负号显示

plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签 plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号

4. 实现灰度图的边缘检测、锐化、模糊

tImage Kernels explained visually (setosa.io)特别好的一个可以实现图像基本变化的网站，支持锐化、边缘检测、模糊、底部轮廓检测、左侧轮廓检测、右侧轮廓检测、上部轮廓检测、浮雕八种图像变化方式，并且网站都有对应卷积核，所以我们来实战一下

import numpy as np
import torch
from torch import nn
from torch.autograd import Variable
from PIL import Image
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
# 加载图片
file_path = 'OIP-C.jpg'
im = Image.open(file_path).convert('L')
im = im.convert("L")
im = np.array(im, dtype='float32')

plt.subplot(331).set_title('原图')
plt.imshow(im.astype('uint8'), cmap='gray')

im = torch.from_numpy(im.reshape((1, 1, im.shape[0], im.shape[1])))
conv1 = nn.Conv2d(1, 1, 3, bias=False)  # 定义卷积
conv2 = nn.Conv2d(1, 1, 3, bias=False)  # 定义卷积
conv3 = nn.Conv2d(1, 1, 3, bias=False)  # 定义卷积
conv4 = nn.Conv2d(1, 1, 3, bias=False)  # 定义卷积
conv5 = nn.Conv2d(1, 1, 3, bias=False)  # 定义卷积
conv6 = nn.Conv2d(1, 1, 3, bias=False)  # 定义卷积
conv7 = nn.Conv2d(1, 1, 3, bias=False)  # 定义卷积
conv8 = nn.Conv2d(1, 1, 3, bias=False)  # 定义卷积

bottom_sobel = np.array([[-1, -2, -1],
                         [0, 0, 0],
                         [1, 2, 1]], dtype='float32').reshape((1, 1, 3, 3))
conv1.weight.data = torch.from_numpy(bottom_sobel)
left_sobel = np.array([[1, 0, -1],
                       [2, 0, -2],
                       [1, 0, -1]], dtype='float32').reshape((1, 1, 3, 3))
conv2.weight.data = torch.from_numpy(left_sobel)
right_sobel = np.array([[-1, 0, 1],
                        [-2, 0, 2],
                        [-1, 0, 1]], dtype='float32').reshape((1, 1, 3, 3))
conv3.weight.data = torch.from_numpy(right_sobel)

top_sobel = np.array([[-1, 2, 1],
                      [0, 0, 0],
                      [-1, -2, -1]], dtype='float32').reshape((1, 1, 3, 3))
conv4.weight.data = torch.from_numpy(top_sobel)

sharpen = np.array([[0, -1, 0],
                    [-1, 5, -1],
                    [0, -1, 0]], dtype='float32').reshape((1, 1, 3, 3))
conv5.weight.data = torch.from_numpy(sharpen)
blur = np.array([[0.0625, 0.125, 0.0625],
                 [0.125, 0.25, 0.125],
                 [0.0625, 0.125, 0.0625]], dtype='float32').reshape((1, 1, 3, 3))
conv6.weight.data = torch.from_numpy(blur)
emboss = np.array([[-2, -1, 0],
                   [-1, 1, 1],
                   [0, 1, 2]], dtype='float32').reshape((1, 1, 3, 3))
conv7.weight.data = torch.from_numpy(emboss)
outline = np.array([[-1, -1, -1],
                    [-1, 8, -1],
                    [-1, -1, -1]], dtype='float32').reshape((1, 1, 3, 3))
conv8.weight.data = torch.from_numpy(outline)

y1 = conv1(Variable(im)).data.squeeze().numpy()
y2 = conv2(Variable(im)).data.squeeze().numpy()
y3 = conv3(Variable(im)).data.squeeze().numpy()
y4 = conv4(Variable(im)).data.squeeze().numpy()
y5 = conv5(Variable(im)).data.squeeze().numpy()
y6 = conv6(Variable(im)).data.squeeze().numpy()
y7 = conv7(Variable(im)).data.squeeze().numpy()
y8 = conv8(Variable(im)).data.squeeze().numpy()

# 可视化
plt.subplot(332).set_title('底部轮廓检测')
plt.imshow(y1, cmap='gray')
plt.subplot(333).set_title('左侧轮廓检测')
plt.imshow(y2, cmap='gray')
plt.subplot(334).set_title('右侧轮廓检测')
plt.imshow(y3, cmap='gray')
plt.subplot(335).set_title('上部轮廓检测')
plt.imshow(y4, cmap='gray')
plt.subplot(336).set_title('锐化')
plt.imshow(y5, cmap='gray')
plt.subplot(337).set_title('模糊')
plt.imshow(y6, cmap='gray')
plt.subplot(338).set_title('浮雕')
plt.imshow(y7, cmap='gray')
plt.subplot(339).set_title('边缘检测')
plt.imshow(y8, cmap='gray')
plt.subplots_adjust(wspace=0.5, hspace=0.5)
plt.show()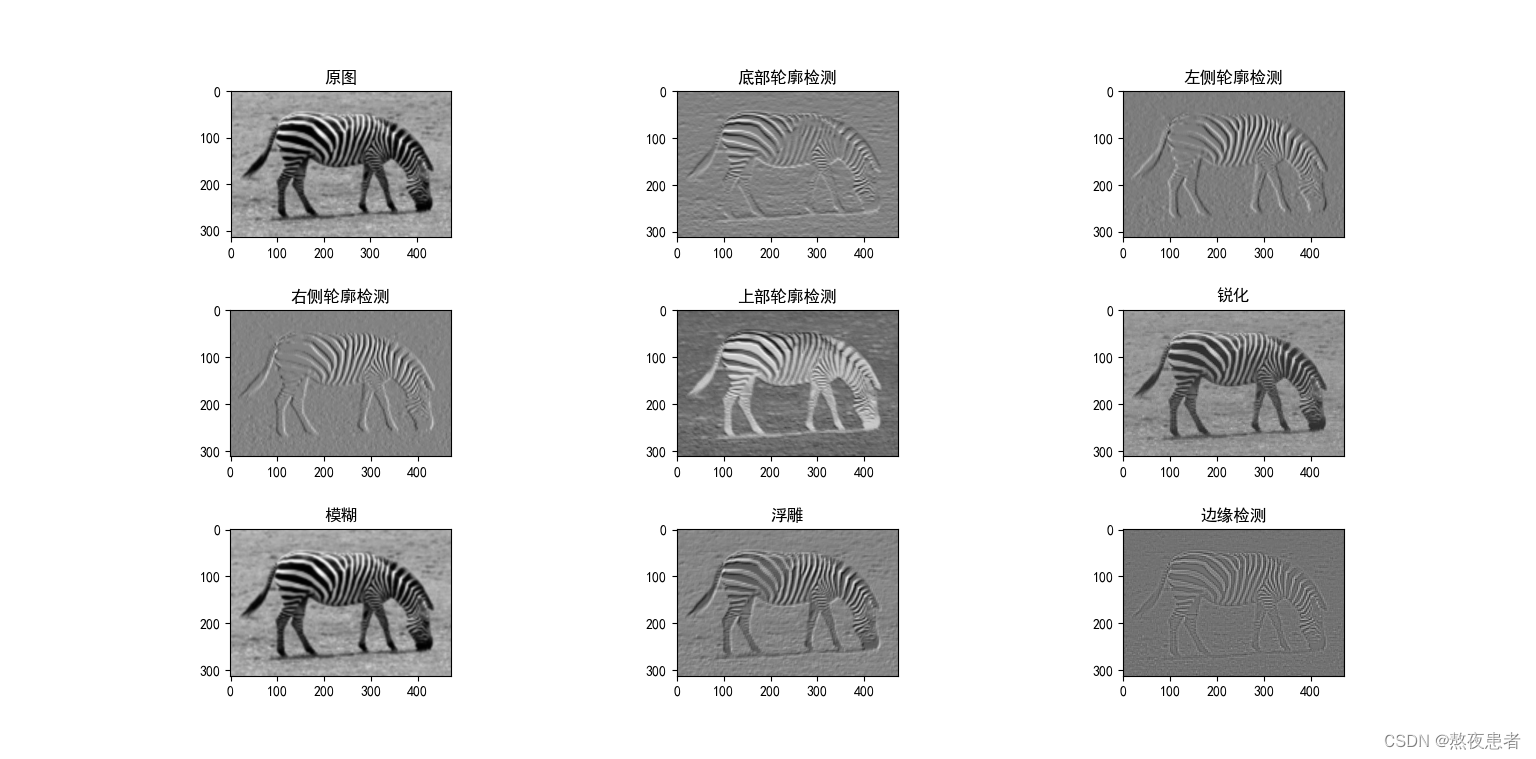

我们放大边缘检测的结果:

修改一下参数

突然就发现好像这个就没有边缘检测的效果了，所以调节卷积核的初始化权重参数，是可以影响特征提取效果。因为这个照片像素不太好我们换一个照片再试试边缘检测.

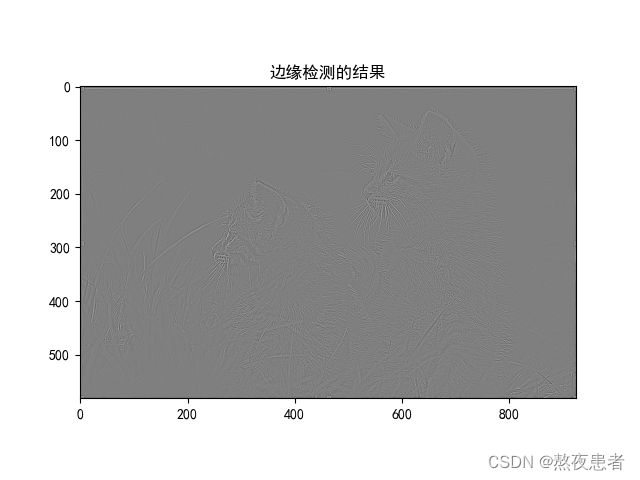
由对比可以发现，卷积核提取特征的效果和分辨率相关，卷积核的大小和特征提取效果与图像的分辨率有一定的相关性。较大的卷积核通常可以捕捉到更大尺度的特征，而较小的卷积核通常可以捕捉到更细微的细节。

同时也可以对RGB图像就行卷积就把通道改成三个即可

import numpy as np
import torch
from torch import nn
from torch.autograd import Variable
from PIL import Image
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
# 加载图片
file_path = 'OIP-C.jpg'
im = Image.open(file_path)
im = np.array(im, dtype='float32')
im = np.transpose(im, (2, 1, 0))
im = im[np.newaxis, :]
im = torch.from_numpy(im)
conv1 = nn.Conv2d(3, 3, 3, bias=False)  # 定义卷积
outline = np.array([[[-1, -1, -1],
                     [-1, 8, -1],
                     [-1, -1, -1]],
                    [[-1, -1, -1],
                     [-1, 8, -1],
                     [-1, -1, -1]],
                    [[-1, -1, -1],
                     [-1, 8, -1],
                     [-1, -1, -1]]]
                   , dtype='float32').reshape((1, 3, 3, 3))
conv1.weight.data = torch.from_numpy(outline)

y1 = conv1(Variable(im)).data.squeeze().numpy()
# 可视化
plt.imshow(y1, cmap='gray')
plt.show()

原图和结果如下：

5. 总结不同卷积核的特征和作用

就以Image Kernels explained visually (setosa.io)的9个卷积核为例：

（1）模糊的作用

（2）底部轮廓检测的作用

（3）浮雕

（4）不变

（5）左侧轮廓检测

（6）边缘检测

（7）右侧轮廓检测

（8）锐化

（9）上部轮廓检测

总结

因为我嗯...比较菜，代码是复刻的，自己尝试写了一下午了，没啥思路，但是看他代码看了不到半小时我就会了，还是敲代码的少，还是得练啊，这次作业从写的时候就在想为什么这样，这样一定好么，这种打破砂锅问到底的思路去写的，就导致写的效率不高，但是收获很大，对于卷积神经网络的大体也有了一定的了解，浅浅立个flag，这两周找时间把前馈神经网络之前的知识点总结一下画个思维导图啥的，课程走一半了，必须得兼顾后面新学的知识的掌握和前面旧知识的牢固！