一、什么是拓扑排序
在图论中,拓扑排序(Topological Sorting)是一个有向无环图(DAG, Directed Acyclic Graph)的所有顶点的线性序列。且该序列必须满足下面两个条件:
- 每个顶点出现且只出现一次。
- 若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面。
【注】:有向无环图(DAG)才有拓扑排序,非DAG图没有拓扑排序一说。
例如,下面这个图,
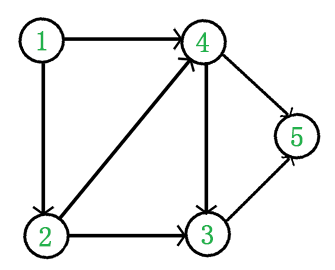
它是一个 DAG 图,那么如何写出它的拓扑排序呢?这里说一种比较常用的方法:
- 从 DAG 图中选择一个 没有前驱(即入度为0)的顶点并输出。
- 从图中删除该顶点和所有以它为起点的有向边。
- 重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为1. 止。后一种情况说明有向图中必然存在环。
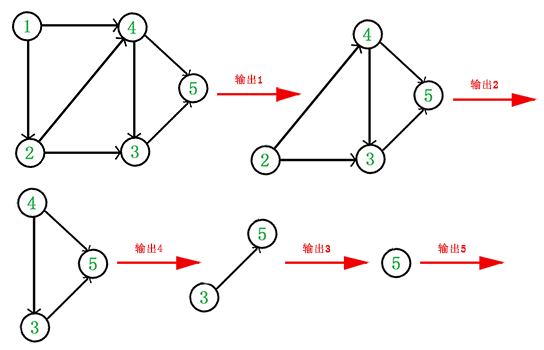
于是,得到拓扑排序后的结果是 { 1, 2, 4, 3, 5 }。
通常,一个有向无环图可以有一个或多个拓扑排序序列。
二、拓扑排序的应用场景
拓扑排序通常用来“排序”具有依赖关系的任务。
比如在项目管理 (Project Management)中,如果用一个DAG图来表示一个工程,其中每个顶点表示工程中的一个任务,用有向边表示在做任务 B 之前必须先完成任务 A。故在这个工程中,任意两个任务要么具有确定的先后关系,要么是没有关系,绝对不存在互相矛盾的关系(即环路)。
在教育领域,拓扑排序也有广泛的应用。考虑一个大学的课程结构,某些课程可能需要先修其他课程。例如,学习“高级数学”可能需要先学习“基础数学”。为了制定一个合理的课程表,我们需要确定一个课程的顺序,确保每个课程在其所有先修课程之后才被安排。这正是拓扑排序的应用场景。
基于的遗传算法多式联运路径优化问题(Multimodal Transportation Path Optimization)中,染色体编码方式是基于拓扑排序的(Population Initialization Based on Topological Sorting)。
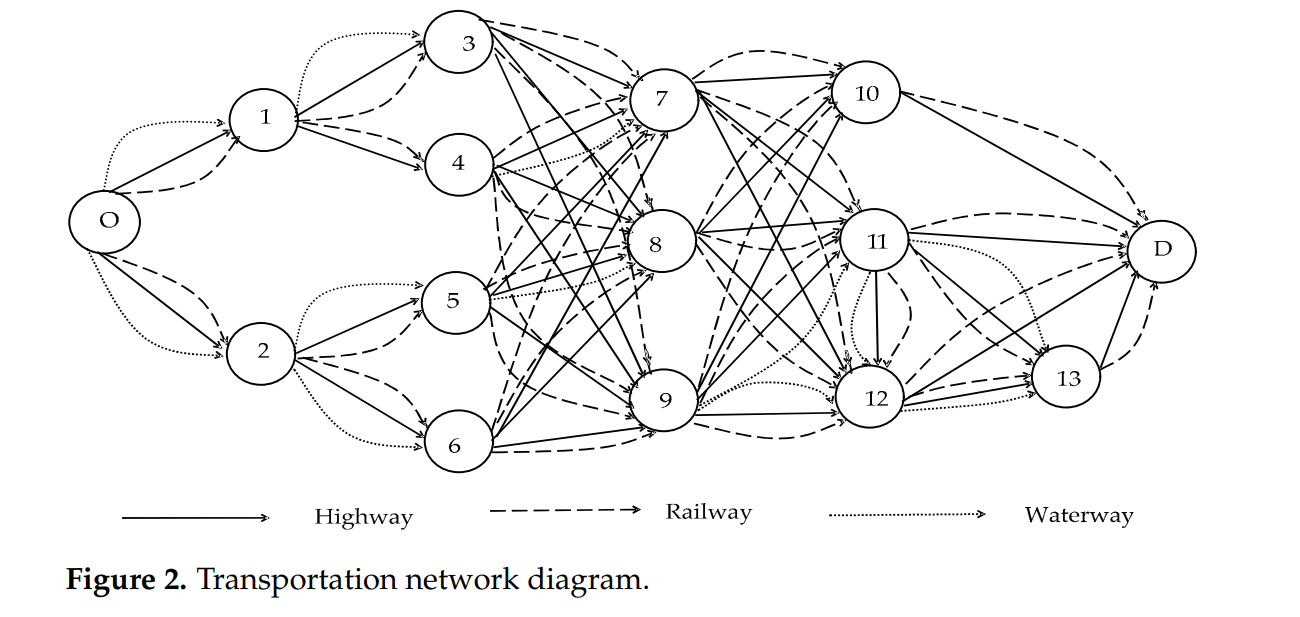
The nodes in the multimodal transportation are arranged in a certain order. In order to ensure the feasibility of the solutions, the initial population is generated based on topological sorting rules to suppress the generation of illegal schemes. The multimodal transportation topology order is obtained by the following methods:
- Design the transportation paths in the transportation diagram into a directed
acyclic graph; - Place the directed acyclic graph in the topological sorting sequence to obtain the
topological sorting of the network graph.
三、拓扑排序的实现(基于Python+Networkx)
import networkx as nx
from matplotlib import pyplot as plt
# 初始化一个有向图
graph = nx.DiGraph()
# 添加边(node1,node2, 权重)
graph.add_weighted_edges_from(
[
(1, 2, 50),
(1, 3, 60),
(2, 4, 65),
(2, 5, 40),
(3, 4, 52),
(3, 7, 45),
(4, 5, 50),
(4, 6, 30),
(4, 7, 42),
(5, 6, 70)
]
)
# 指定顶点位置
pos = {
1: (2.5, 10),
2: (0, 5),
3: (7.5, 10),
4: (5, 5),
5: (2.5, 0),
6: (7.5, 0),
7: (10, 5)
}
#显示graph
nx.draw_networkx(graph, pos=pos, with_labels=True)
labels = nx.get_edge_attributes(graph, 'weight') # 获取边的权值
nx.draw_networkx_edge_labels(graph, pos, edge_labels=labels) # 显示边的权值
# 这个graph拓扑排序序列不唯一,这里只给出一种
'扑排序序列:',list(nx.topological_sort(graph))
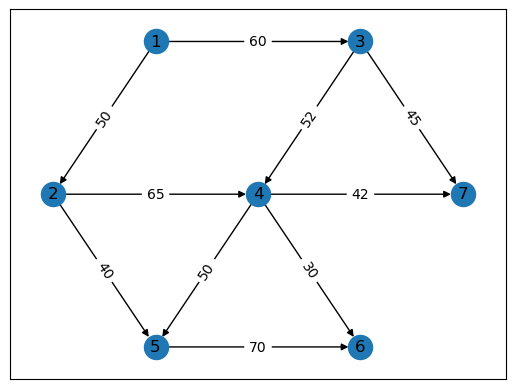
(‘扑排序序列:’, [1, 2, 3, 4, 5, 7, 6])
另外,拓扑排序还可以采用 深度优先搜索(DFS)的思想来实现,详见《topological sorting via DFS》。
参考:
- https://blog.csdn.net/lisonglisonglisong/article/details/45543451
- Zhang X, Jin F Y, Yuan X M, et al. Low-Carbon Multimodal Transportation Path Optimization under Dual Uncertainty of Demand and Time[J/OL]. Sustainability, 2021, 13(15): 8180. https://doi.org/10.3390/su13158180.