*本文为博主本人校内的离散数学专业课的实践作业。由于实验步骤已经比较详细,故不再对该实验额外提供详解,本文仅提供填写的实验报告内容与代码部分,以供有需要的同学学习、参考。
--------------------------------------
编程语言:Java SE
编译环境:jdk 8
相关文章:离散数学实践(1)-编程实现利用真值表法求主析取范式以及主合取范式
目录
一、实验目的
二、实验内容
三、实验步骤及实验结果
1、Java类与接口的设计
(1)设计六个Java类。
(2)类Matrix
(3)类IsReflexive
(4)类IsSymmetry
(5)类IsTransitivity
(6)类Test
2、设计步骤和思路(类TestMain)
3、运行结果
四、总结
一、实验目的
1、理解二元关系的矩阵表示
2、理解二元关系的自反性、反自反性、对称性、反对称性及传递性
二、实验内容
1、用矩阵表示二元关系
2、通过矩阵的特征判断二元关系所具有的性质
3、运用二维数组实现矩阵的输入,然后判断自反性,反自反性,对称性,反对称性,传递性
三、实验步骤及实验结果
1、Java类与接口的设计
(1)设计六个Java类。
包括用于实现四个关系性质判断功能类(类IsReflexive,类IsSymmetry,类IsTransitivity,类Matrix),一个辅助类Test和一个测试类TestMain。
TestMain类中设计main方法,在main方法中搭建程序的主体框架,包括多组输入,实例化Matrix类以访问关系矩阵对象,实例化自反性、传递性与对称性对象。
(2)类Matrix
定义成员变量:关系矩阵的阶数n,关系矩阵二维数组array,并设置访问限定修饰符private和protected将n和array封装。构造方法接收main方法传入的矩阵阶数n,并创建数组对象,以存储用户输入的矩阵值。
定义成员方法:出于封装的考虑,设计public的方法接口getN()和getArray(),以及矩阵的输出方法,用于在用户输入完毕矩阵后,将矩阵展现出来。输出二维数组也可以调用Arrays.deepToString()完成。
package com.lisan;
import java.util.Arrays;
public class Matrix {
private int n; //阶数
protected int[][] array; //矩阵二维数组
public int getN() {
return n;
}
public Matrix(int n) {
this.n = n;
this.array = new int[n][n];
}
public int[][] getArray() {
return array;
}
//输出矩阵
public void printMatrix() {
System.out.println("关系矩阵为:");
for (int[] ret : array) {
for (int x : ret) {
System.out.print(x + " ");
}
System.out.println();
}
}
}
(3)类IsReflexive
该类为继承类,继承父类Matrix,以复用Matrix类中的成员。可以理解为:一个自反关系类,可以实例化出一个自反关系对象。
定义成员变量: reflexive(自反),antiReFlexive(反自反)。初始值均为false。
定义成员方法:
public boolean isRef():用于判断关系是否为自反性。根据输入只能为0或1两个值,因此自反矩阵的主对角线元素值均为1。遍历二维数组,用flag标记该关系的主对角线值是否均为1.若均为1,则更改reflexive属性为true,意为该关系是自反性的;否则reflexive仍为false。最终将属性reflexive值返回。
public boolean isAntiRef():用于判断关系是否为反自反性。思路同上,反自反矩阵的主对角线元素值均为0.遍历二维数组,用flag标记该关系的主对角线值是否均为0.若均为0,则更改antiReFlexive属性为true,意为该关系是反自反性的;否则antiReFlexive仍为false。最终将属性antiReFlexive值返回。
package com.lisan;
public class IsReflexive extends Matrix {
boolean reflexive; //自反性
boolean antiReflexive; //反自反性
public IsReflexive(int n,int[][] array) {
super(n);
super.array = array;
}
public boolean isRef() {
boolean flag = true;
//自反矩阵主对角线元素全为1
for (int i = 0; i < array.length; i++) {
if (array[i][i] != 1) {
flag = false;
break;
}
}
if (flag) {
this.reflexive = true; //是自反的
}
return this.reflexive;
}
public boolean isAntiRef() {
boolean flag = true;
//反自反矩阵主对角线元素全为0
for (int i = 0; i < array.length; i++) {
if (array[i][i] != 0) {
flag = false;
break;
}
}
if (flag) {
this.antiReflexive = true; //是反自反的
}
return this.antiReflexive;
}
}
(4)类IsSymmetry
该类同样继承父类Matrix。可以理解为:一个对称关系类。
定义成员变量:symmetry(对称),skewSymmetry(反对称)。初始值均为false。
定义成员方法:
public boolean isSymmetry() :用于判断关系是否为对称性。遍历二维数组,用flag标记该关系对称矩阵array[i][j] == array[j][i].若成立,则更改symmetry属性为true,意为该关系是对称性的;否则symmetry仍为false。最终将属性this.symmetry值返回。
public boolean isAntiSymmetry():用于判断关系是否为反对称性。在反对称矩阵中,i != j时,array[i][j]和array[j][i]不同时为1。遍历二维数组,用flag标记反对称条件是否成立。若成立,则更改this.skewSymmetry属性为true,意为该关系是反对称性的;否则仍为false。最终将this.skewSymmetry值返回。
package com.lisan;
public class IsSymmetry extends Matrix {
boolean symmetry; //对称性
boolean skewSymmetry; //反对称性
public IsSymmetry(int n,int[][] array) {
super(n);
super.array = array;
}
public boolean isSymmetry() {
boolean flag = true;
//对称矩阵array[i][j] == array[j][i]
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array[i].length; j++) {
if(array[i][j] != array[j][i]) {
flag = false;
break;
}
}
}
if(flag) {
this.symmetry = true;
}
return this.symmetry;
}
public boolean isAntiSymmetry() {
boolean flag = true;
//反对称矩阵中i != j时,array[i][j]和array[j][i]不同时为1
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array[i].length; j++) {
if(i != j) {
if (array[i][j] == 1 && array[j][i] == 1) {
flag = false;
break;
}
}
if(!flag) {
break;
}
}
}
if(flag) {
this.skewSymmetry = true;
}
return this.skewSymmetry;
}
}
(5)类IsTransitivity
该类同样继承父类Matrix。可以理解为:一个对传递关系类。
定义成员变量:transitivity(传递)。初始值均为false。
定义成员方法:
public boolean isTransitivity() :用于判断关系是否为传递性。已知在传递矩阵中,若array[i][j]==1且array[j][k]==1,则a[i][k]也为1。遍历二维数组,用flag标记该关系对称矩阵是否满足传递性的条件。若成立,则更改transitivity属性为true,意为该关系是传递的;否则transitivity仍为false。最终将属性this.transitivity值返回。
package com.lisan;
public class IsTransitivity extends Matrix{
boolean transitivity; //传递性
public IsTransitivity(int n,int[][] array) {
super(n);
super.array = array;
}
public boolean isTransitivity() {
int n = getN();
boolean flag = true;
//传递矩阵若array[i][j]==1且array[j][k]==1,则a[i][k]也为1
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
for (int l = 0; l < n; l++) {
if (array[i][j] == 1 && array[j][l] == 1) {
if(array[i][l] != 1) {
flag = false;
break;
}
}
}
if(!flag) {
break;
}
}
if(!flag) {
break;
}
}
if(flag) {
this.transitivity = true;
}
return transitivity;
}
}
(6)类Test
该类用于依次测试各个类功能与接口是否能正常运行,不作为最终的实验功能实现。
2、设计步骤和思路(类TestMain)
(1)输入矩阵真值
在main方法中进行输入。首先输入关系矩阵阶数n,再实例化Matrix对象,构造一个n阶的二维数组。调用matrix.getArray()方法接收创建的数组对象的引用。
然后用户输入关系中的真值。规定:只能输入0或1.检查用户输入是否有误,若有则提示用户重新输入正确的值。
(2)输出用户输入的数组值。
(3)实例化自反关系对象:IsReflexive ref = new IsReflexive(n,array);传入阶数n与引用array,调用ref的成员方法,依次判断ref是否为自反关系、反自反关系。若ref.reflexive和ref.antiReflexive均为false,则说明它既不是自反关系也不是反自反关系。输出结果。
(4)实例化对称关系对象与传递关系对象。同理,分别调用对象的成员方法,依次判断它是否为对称关系、反对称关系、传递关系。若对称关系判断中symmetry和skewSymmetry均为false,则说明它既不是对称关系也不是反对称关系。输出结果。
package com.lisan;
import java.util.Scanner;
public class TestMain {
public static void main(String[] args) {
Scanner reader = new Scanner(System.in);
//输入关系矩阵
System.out.println("请输入关系矩阵阶数:");
int n = reader.nextInt();
Matrix matrix = new Matrix(n);
int[][] array = matrix.getArray();
System.out.println("请输入关系矩阵R (0或1):");
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array[i].length; j++) {
array[i][j] = reader.nextInt();
while(array[i][j] != 0 && array[i][j] != 1) {
System.out.println("输入有误!重新输入!");
array[i][j] = reader.nextInt();
}
}
}
//System.out.println(matrix);
matrix.printMatrix();
//System.out.println(Arrays.deepToString(array));
System.out.print("是否自反:");
IsReflexive ref = new IsReflexive(n,array);
if(ref.isRef()) {
System.out.println("自反关系!");
} else if(ref.isAntiRef()) {
System.out.println("反自反关系!");
} else {
System.out.println("既不自反也不反自反!");
}
System.out.print("是否对称:");
IsSymmetry sym = new IsSymmetry(n,array);
if(sym.isSymmetry()) {
System.out.println("对称关系!");
} else if (sym.isAntiSymmetry()) {
System.out.println("反对称关系!");
} else {
System.out.println("既不对称也不反对称!");
}
System.out.print("是否传递:");
IsTransitivity tran = new IsTransitivity(n,array);
if(tran.isTransitivity()) {
System.out.println("传递关系!");
} else {
System.out.println("不是传递关系!");
}
}
}
3、运行结果
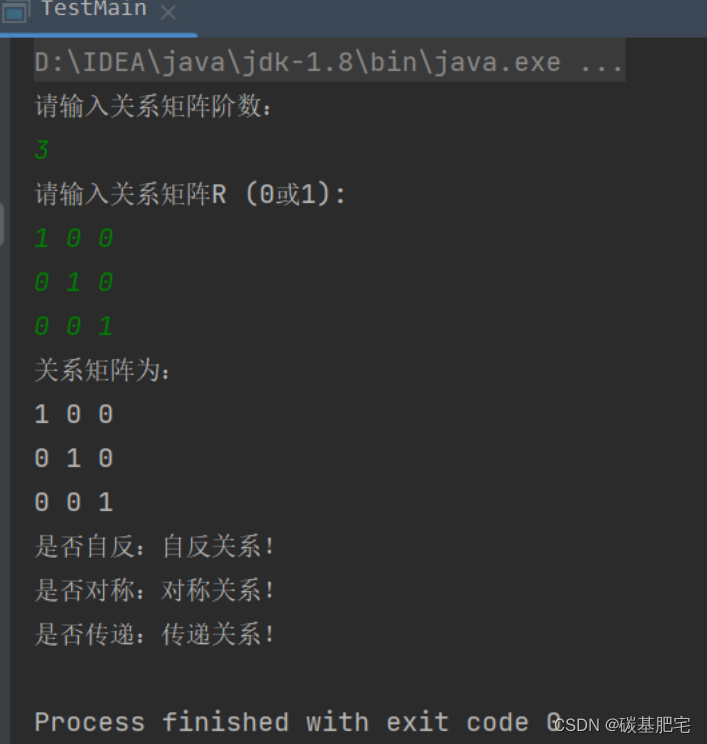
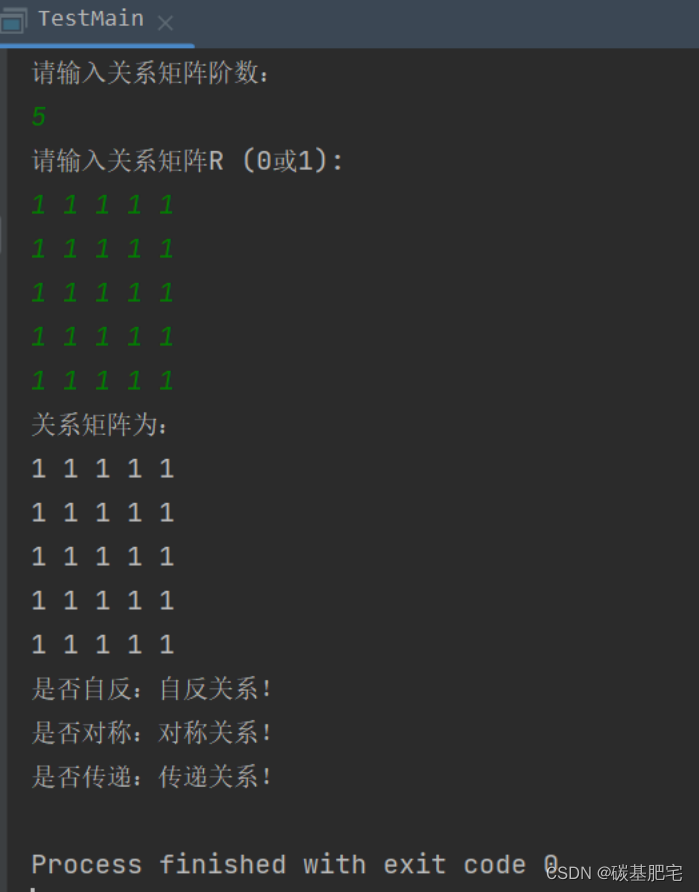
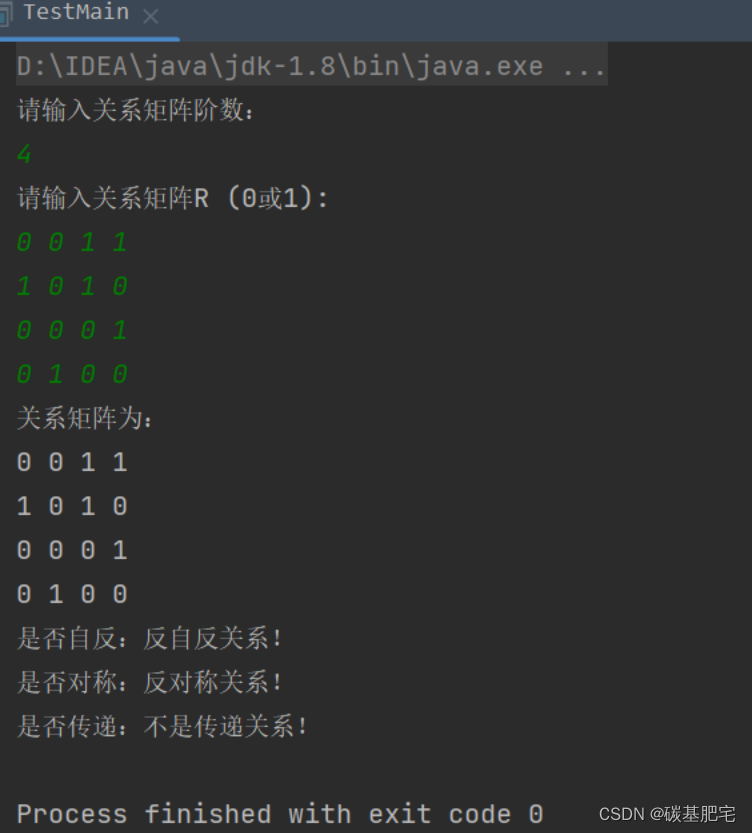
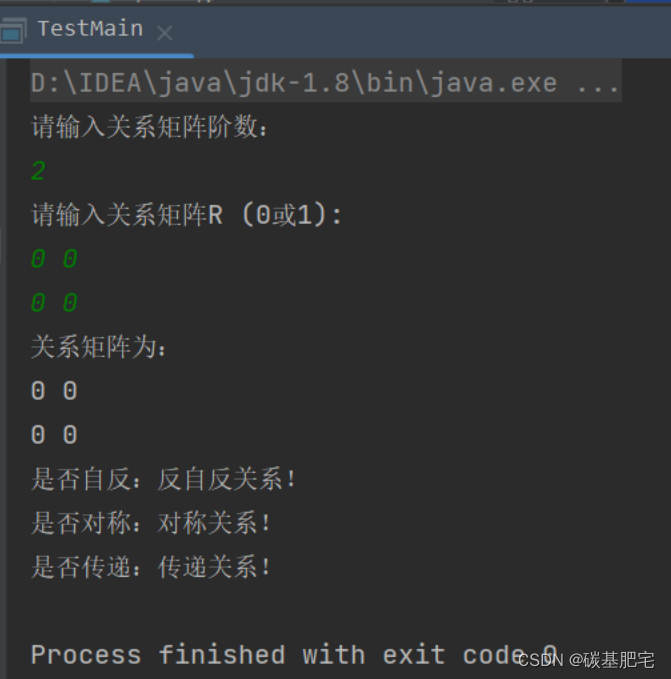
四、总结
- 经过编程,从代码的角度考虑离散数学问题,更熟练地掌握了关系性质判断的原理。
- Java类面向对象的思维得到了很好的体现。
- 自反:主对角线元素全是1
- 反自反:主对角线元素全是0
- 对称:矩阵是对称矩阵(R的逆等于R)
- 反对称:若rij=1, 且i≠j, 则rji=0
- 传递:对M2中1所在位置,M中相应位置都是1
经过实践作业,对以上离散数学知识点的理解更为深入了。可以与对书本上的书面作业融会贯通。
![VM虚拟机逆向 --- [NCTF 2018]wcyvm 复现](https://img-blog.csdnimg.cn/0ffd3f35962d462b9ec57a070bed2c6b.png)