稠密连接网络DenseNet
- 1. 从ResNet到DenseNet
- 2. 稠密块体
- 3. 过渡层
- 4. DenseNet模型
- 5. 训练模型
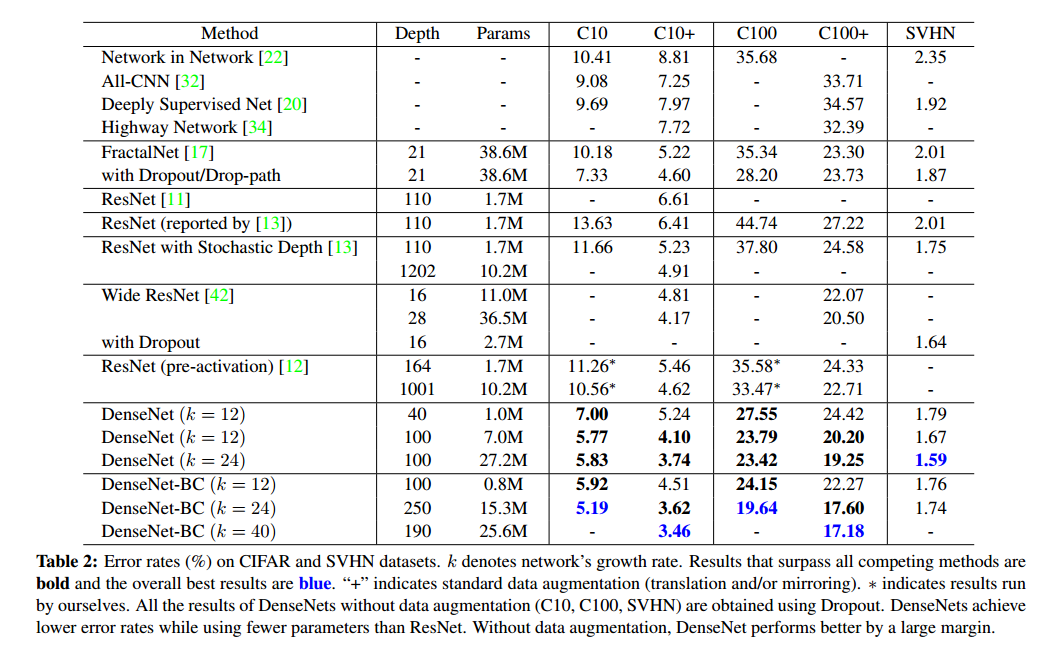
CIFAR 和 SVHN 数据集上的错误率 (%)。DenseNet 比 ResNet 使用更少的参数,同时实现了更低的错误率。在没有数据增强的情况下,DenseNet 的性能大幅提高。
1. 从ResNet到DenseNet
稠密连接网络在某种程度上是ResNet的逻辑扩展。
回想一下任意函数的泰勒展开式,它把这个函数分解成越来越高阶的项。在x接近0时,
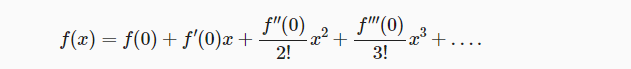
ResNet将函数展开为

ResNet将 f 分解为两部分:一个简单的线性项和一个复杂的非线性项。
那么再向前拓展一步,如果我们想将 f 拓展成超过两部分的信息呢? 一种方案便是DenseNet,使用连结。
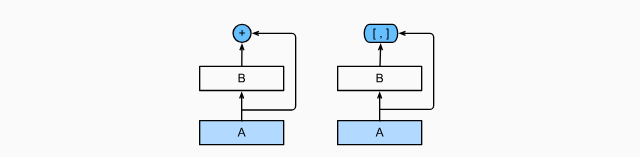
执行从x到其展开式的映射
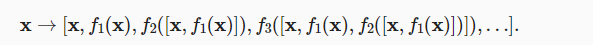
最后,将这些展开式结合到多层感知机中,再次减少特征的数量。
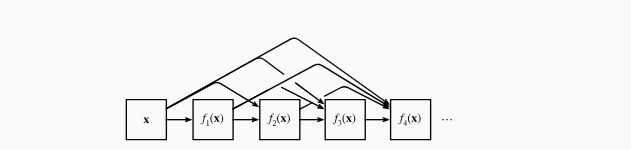
稠密网络主要由2部分构成:
- 稠密块(dense block):定义如何连接输入和输出
- 过渡层(transition layer):控制通道数量,使其不会太复杂。
2. 稠密块体
稠密块每一层都将所有前面的特征图作为输入

DenseNet使用了ResNet改良版的“批量规范化、激活和卷积”架构
# 泰勒公式
"""
稠密网络:
1、稠密块:定义如果连接输入和输出
2、过渡层:后者控制通道数
"""
import torch
from torch import nn
from d2l import torch as d2l
def conv_block(input_channels, num_channels):
return nn.Sequential(
nn.BatchNorm2d(input_channels), nn.ReLU(),
nn.Conv2d(input_channels, num_channels, kernel_size=3, padding=1))
一个稠密块由多个卷积块组成,每个卷积块使用相同数量的输出通道。在前向传播中,将每个卷积块的输入和输出在通道维上连结。
# 稠密块
class DenseBlock(nn.Module):
def __init__(self, num_convs, input_channels, num_channels):
super(DenseBlock, self).__init__()
layer = []
for i in range(num_convs):
# 稠密连接:执行从x到其展开式的映射,即每个卷积块的输入和输出在通道维度上连接
layer.append(conv_block(i * num_channels + input_channels, num_channels))
self.net = nn.Sequential(*layer)
def forward(self, X):
for blk in self.net:
Y = blk(X)
# 连接通道维度上每个卷积块的输入和输出
X = torch.cat((X, Y), dim=1)
return X
定义一个有2个输出通道数为10的DenseBlock。 使用通道数为3的输入时,我们会得到通道数为3+2x10=23的输出。
卷积块的通道数控制了输出通道数相对于输入通道数的增长,因此也被称为增长率(growth rate)。
# 定义有2个输出通道为10的DenseBlock
# 使用通道数为3的输入,会得到3+2x10=23
# 卷积块的通道数控制了输出通道数相对于输入通道数的增长程度,因此被称为增长率
blk = DenseBlock(2, 3, 10)
X = torch.randn(4, 3, 8, 8)
Y = blk(X)
Y.shape

3. 过渡层
每个稠密块都会带来通道数的增加,使用过多则会过于复杂化模型。
过渡层可以用来控制模型复杂度,它通过1x1卷积层来减小通道数,并使用步幅为2的平均汇聚层减半高和宽,从而进一步降低模型复杂度。
# 过渡层:用来控制模型复杂度
# 1x1卷积层减少通道数,使用步幅为2的平均汇聚层减半高度和宽度
def transition_block(input_channels, num_channels):
return nn.Sequential(
nn.BatchNorm2d(input_channels), nn.ReLU(),
nn.Conv2d(input_channels, num_channels, kernel_size=1),
nn.AvgPool2d(kernel_size=2, stride=2))
对于上一个例子,将通道数从23变为10
# 对于上一个例子,将通道数从23变为10
blk = transition_block(23, 10)
blk(Y).shape

4. DenseNet模型
DenseNet首先使用同ResNet一样的单卷积层和最大汇聚层
# 构建DenseNet
# 首先,使用和ResNet一样的卷积层和最大汇聚层
b1 = nn.Sequential(
nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
nn.BatchNorm2d(64), nn.ReLU(),
nn.AvgPool2d(kernel_size=3, stride=2, padding=1))
DenseNet使用4个稠密块,稠密块里的卷积层通道数(即增长率)设为32,所以每个稠密块将增加128个通道。
在每个模块之间,ResNet通过步幅为2的残差块减小高和宽,DenseNet则使用过渡层来减半高和宽,并减半通道数。
"""
DenseNet使用4个稠密块:
1、稠密块里的卷积层通道数(即增长率)设为32,每个稠密块将增加4x32=128个通道
2、每个模块之间,DenseNet使用过渡层减半高度和宽度,并减半通道数
"""
# num_channels为当前的通道数
# growth_rate为增长率,即输出通道相对于输入通道的增长程度
num_channels, growth_rate = 64, 32
# 4个稠密块,每个稠密块4个卷积层,每个稠密块增加4x32=128个通道
num_convs_in_dense_blocks = [4, 4, 4, 4]
blks = []
for i, num_convs in enumerate(num_convs_in_dense_blocks):
blks.append(DenseBlock(num_convs, num_channels, growth_rate))
# 上一个稠密块的输出通道数
num_channels += num_convs * growth_rate
# 在稠密块之间添加一个过渡层,使通道数减半
if i != len(num_convs_in_dense_blocks) - 1:
blk.append(transition_block(num_channels, num_channels // 2))
num_channels // 2
最后接上全局汇聚层和全连接层来输出结果。
# 最后连接全局汇聚层和全连接层来输出结果
net = nn.Sequential(
b1, *blks,
nn.BatchNorm2d(num_channels), nn.ReLU(),
nn.AdaptiveAvgPool2d((1, 1)),
nn.Flatten(),
nn.Linear(num_channels, 10))
5. 训练模型
定义精度评估函数
"""
定义精度评估函数:
1、将数据集复制到显存中
2、通过调用accuracy计算数据集的精度
"""
def evaluate_accuracy_gpu(net, data_iter, device=None): #@save
# 判断net是否属于torch.nn.Module类
if isinstance(net, nn.Module):
net.eval()
# 如果不在参数选定的设备,将其传输到设备中
if not device:
device = next(iter(net.parameters())).device
# Accumulator是累加器,定义两个变量:正确预测的数量,总预测的数量。
metric = d2l.Accumulator(2)
with torch.no_grad():
for X, y in data_iter:
# 将X, y复制到设备中
if isinstance(X, list):
# BERT微调所需的(之后将介绍)
X = [x.to(device) for x in X]
else:
X = X.to(device)
y = y.to(device)
# 计算正确预测的数量,总预测的数量,并存储到metric中
metric.add(d2l.accuracy(net(X), y), y.numel())
return metric[0] / metric[1]
定义GPU训练函数
"""
定义GPU训练函数:
1、为了使用gpu,首先需要将每一小批量数据移动到指定的设备(例如GPU)上;
2、使用Xavier随机初始化模型参数;
3、使用交叉熵损失函数和小批量随机梯度下降。
"""
#@save
def train_ch6(net, train_iter, test_iter, num_epochs, lr, device):
"""用GPU训练模型(在第六章定义)"""
# 定义初始化参数,对线性层和卷积层生效
def init_weights(m):
if type(m) == nn.Linear or type(m) == nn.Conv2d:
nn.init.xavier_uniform_(m.weight)
net.apply(init_weights)
# 在设备device上进行训练
print('training on', device)
net.to(device)
# 优化器:随机梯度下降
optimizer = torch.optim.SGD(net.parameters(), lr=lr)
# 损失函数:交叉熵损失函数
loss = nn.CrossEntropyLoss()
# Animator为绘图函数
animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
legend=['train loss', 'train acc', 'test acc'])
# 调用Timer函数统计时间
timer, num_batches = d2l.Timer(), len(train_iter)
for epoch in range(num_epochs):
# Accumulator(3)定义3个变量:损失值,正确预测的数量,总预测的数量
metric = d2l.Accumulator(3)
net.train()
# enumerate() 函数用于将一个可遍历的数据对象
for i, (X, y) in enumerate(train_iter):
timer.start() # 进行计时
optimizer.zero_grad() # 梯度清零
X, y = X.to(device), y.to(device) # 将特征和标签转移到device
y_hat = net(X)
l = loss(y_hat, y) # 交叉熵损失
l.backward() # 进行梯度传递返回
optimizer.step()
with torch.no_grad():
# 统计损失、预测正确数和样本数
metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
timer.stop() # 计时结束
train_l = metric[0] / metric[2] # 计算损失
train_acc = metric[1] / metric[2] # 计算精度
# 进行绘图
if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
animator.add(epoch + (i + 1) / num_batches,
(train_l, train_acc, None))
# 测试精度
test_acc = evaluate_accuracy_gpu(net, test_iter)
animator.add(epoch + 1, (None, None, test_acc))
# 输出损失值、训练精度、测试精度
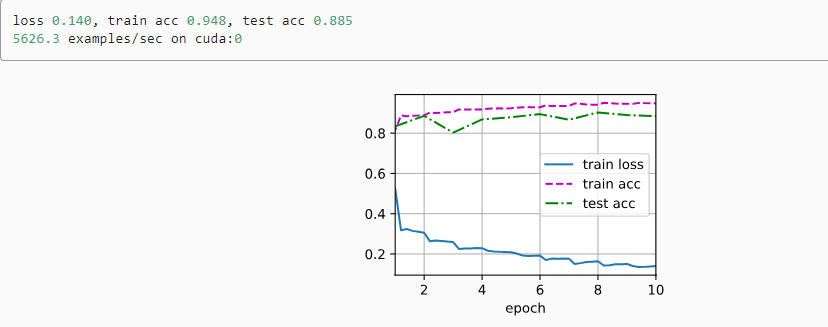
print(f'loss {train_l:.3f}, train acc {train_acc:.3f},'
f'test acc {test_acc:.3f}')
# 设备的计算能力
print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec'
f'on {str(device)}')

由于模型较深,这里将输入高度和宽度从224降为96
# 训练模型
# 由于模型较深,这里将输入高度和宽度从224降为96
lr, num_epochs, batch_size = 0.1, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())