查找

基本概念

查找表，其实就类似于数据库的数据表。
所谓的数据项，就是数据库的一列，而关键字就是key，是唯一的。

查找长度（SL）即key的比较次数，ASL是Average SL

线性表查找

顺序查找

基本的查找算法，如果不会写就废了，注意循环跳出条件：key匹配则跳出

哨兵可以简化代码，本质在于，哨兵和普通元素的逻辑是一致的，但是可以发挥出终止的效果
因此，for循环不需要考虑越界，最后return的时候也不需要判断是否查找成功（哨兵本身的0下标就代表失败）

其实链表里的头结点也是一种哨兵。

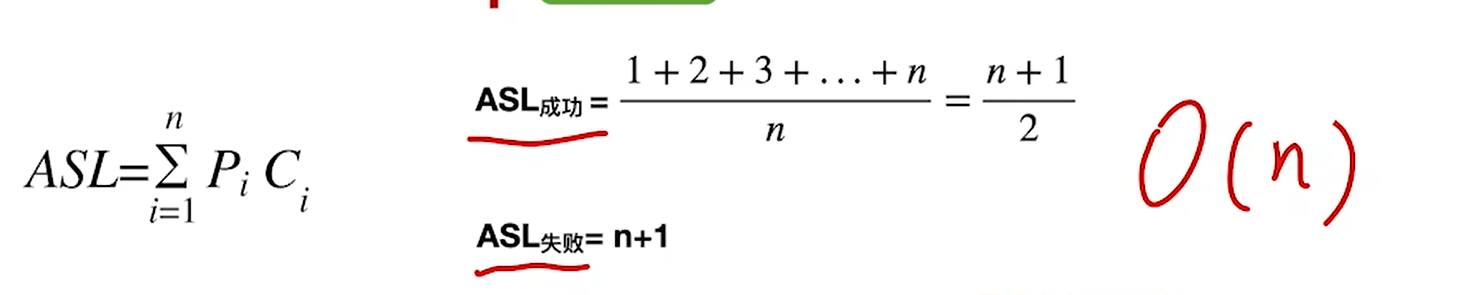
查找的优化思路有二：

1. 有序情况下（假定顺序），如果key已经大于目标key了，那么后面也就没必要继续扫了，即提前终止，可以减少失败ASL
2. 如果已知查找到的概率，那么可以将高概率的排在前面，即提前成功，可以减少成功ASL

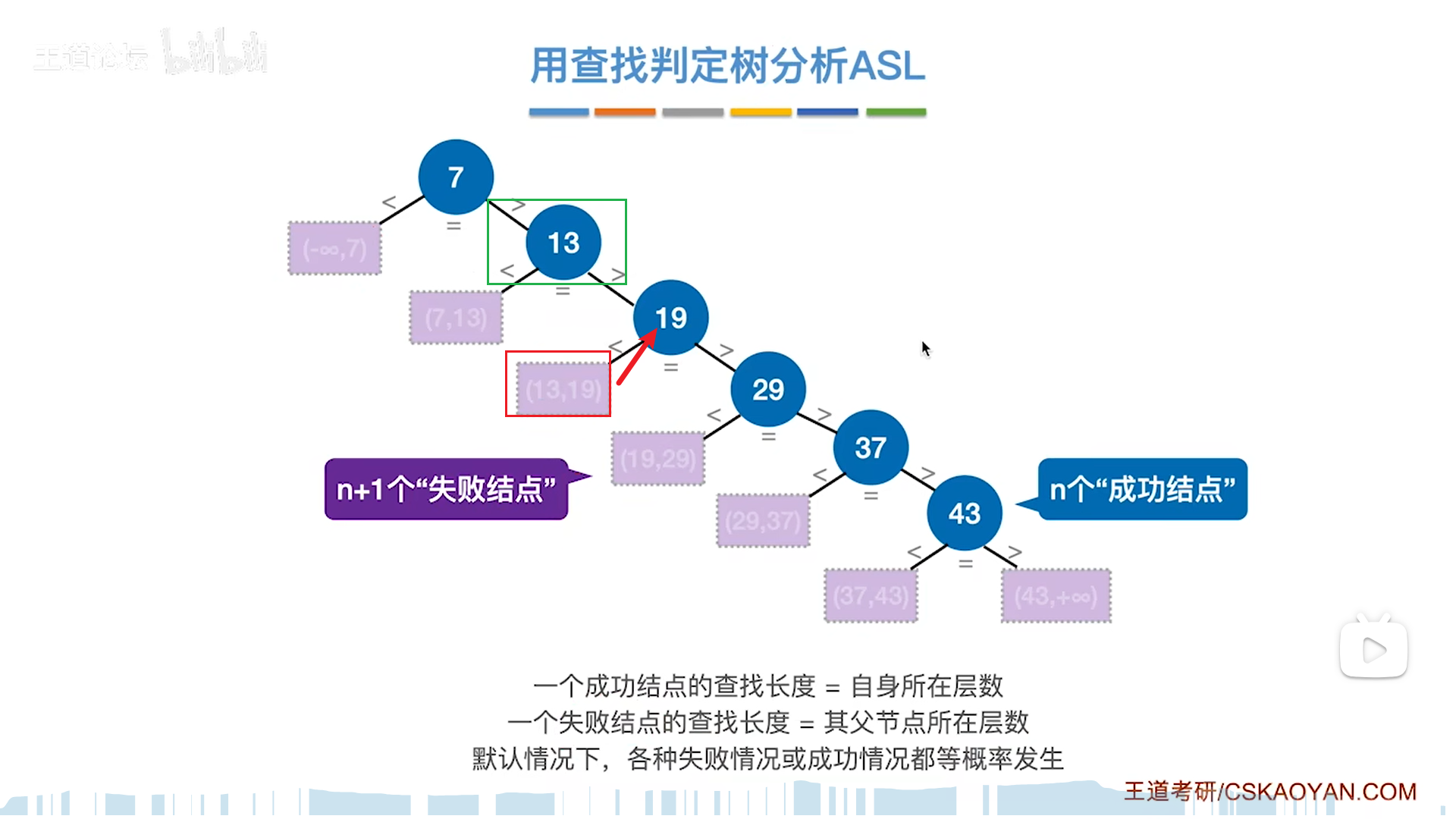
分析ASL的时候可以用判定树来分析，将判定逻辑写成树，分析ASL的思路如下：

1. 成功的ASL，就把n个成功节点加权和，而失败的ASL，就把n+1个失败节点加权和
2. 单个成功节点的SL=高度，而失败节点的SL=父节点高度

折半查找（二分）

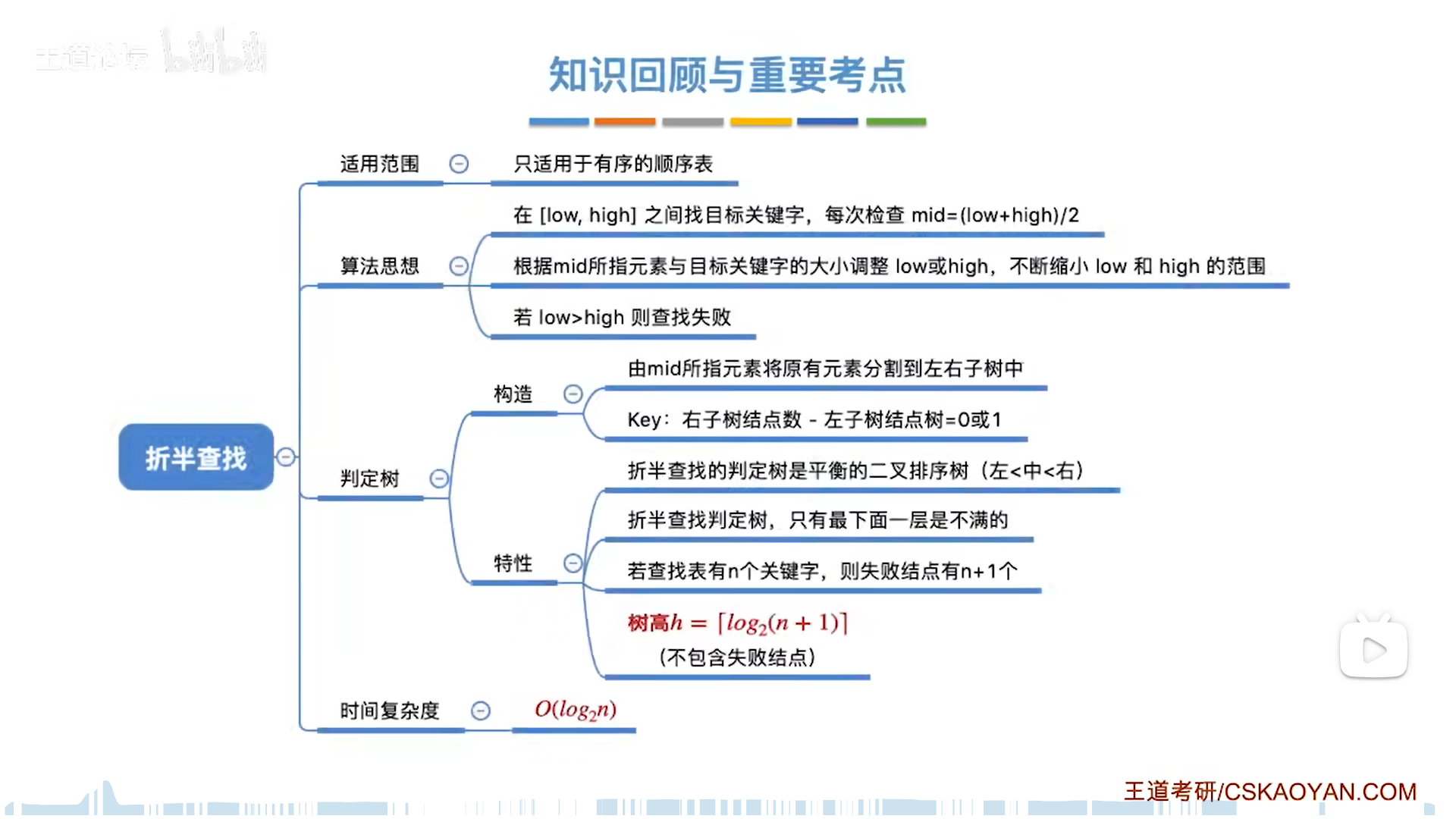
前提是有序。

low和high构成一个闭区间，目标元素只可能在闭区间内，每次要和mid对比。

和mid对比，情况有两大类：

1. 等，则成功
2. 不等，则代表只能在两侧区域，不包括mid，因此边界要调整为mid-1（小），mid+1（大）

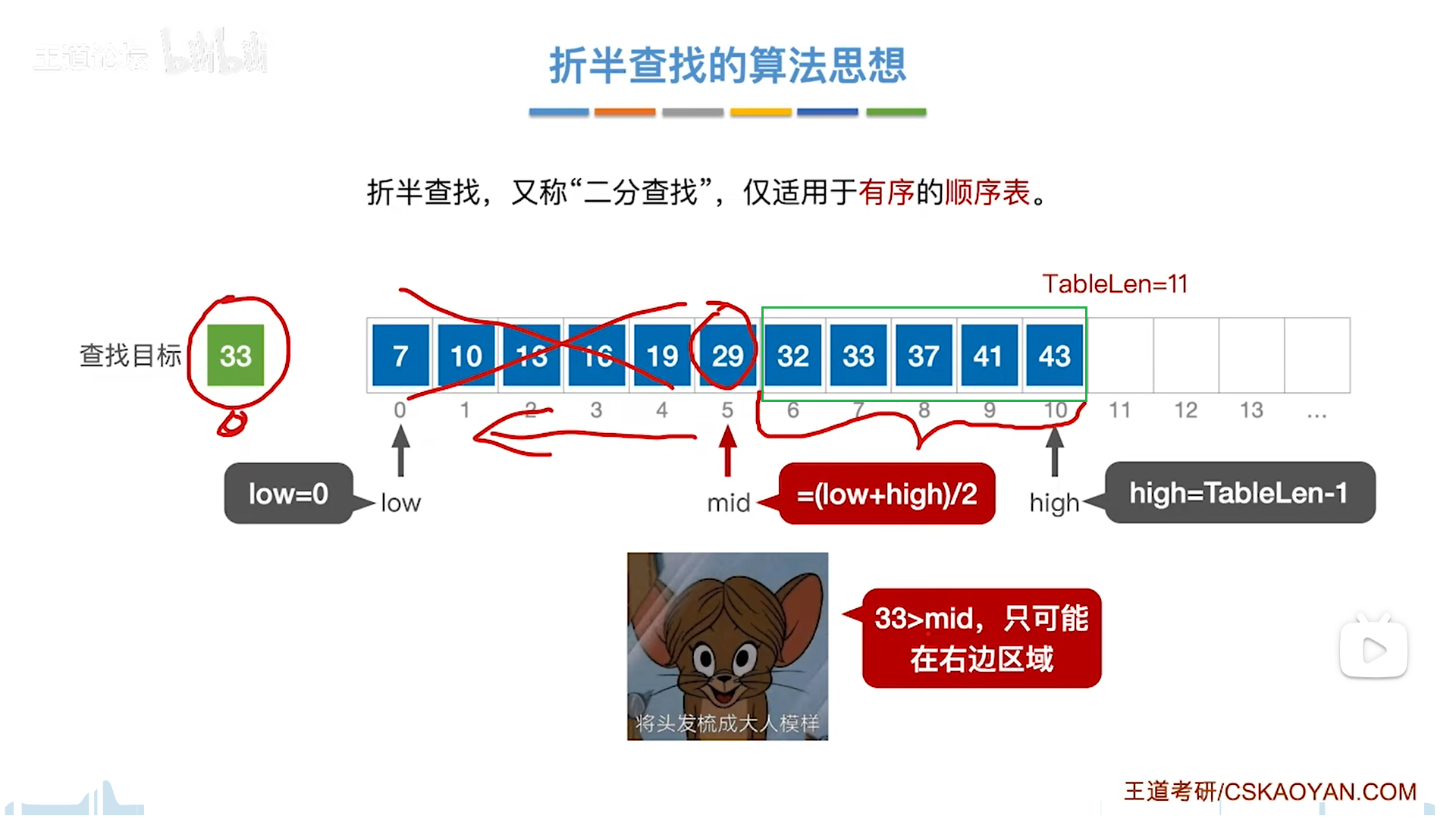
此时你可能会怀疑，最后能不能收敛，如果你是以mid为新边界，下面这种情况可能就无法收敛了，但是如果你去掉mid，即以mid+1为新边界，假设能查到，最坏的情况也一定会收敛到具体的一个点上（此时low==high）

假设查不到，在收敛到具体的一个点后，low和high就要错开，构成low>high的情景，此时直接报错

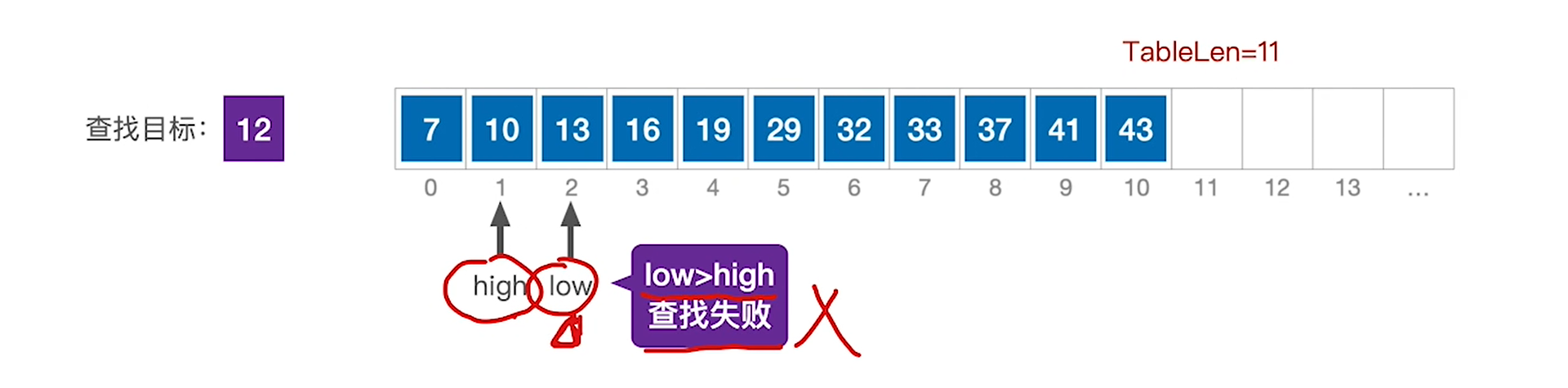
整体来看这个算法，过程如下：

1. 考察区域从全部收敛到-1
   • 极限情况：low≤high
   • 一定会不断收缩，一定可以判定完最后一个点
   • 之后继续走的话，low和high会交错，退出循环
2. 在收敛过程中，如果成功则提前退出循环

因此这个算法是完美无缺的，可以全覆盖所有可能。

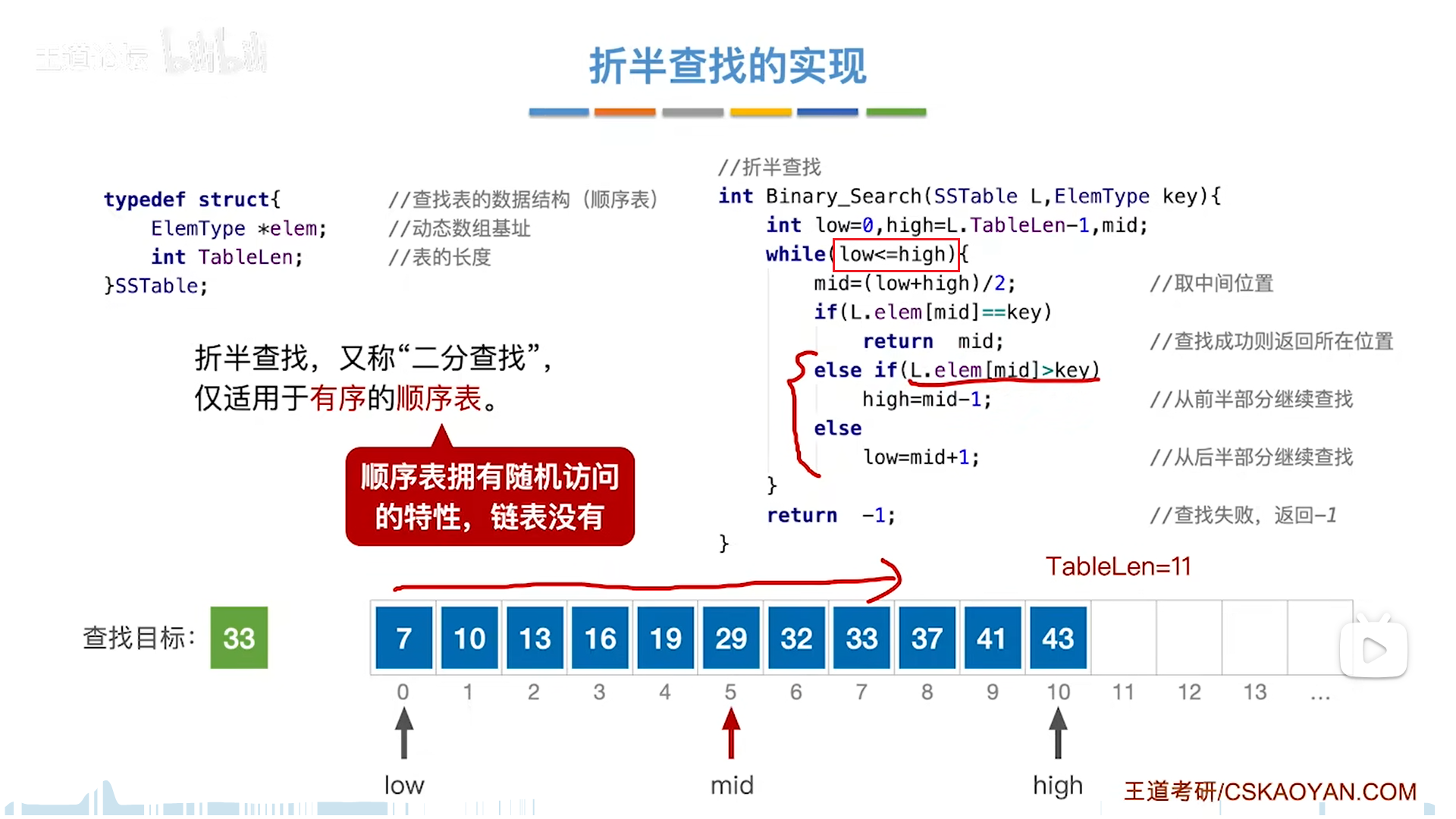
分析效率继续用判定树，这个判定树是非常的神奇好用，把成功节点（mid）逐层展开，再补上失败节点就如下图

需要注意的是，假如总结点数量为偶数个，那么考虑到mid是向下取整，就会出现右子树=左子树+1的现象，不可能更多了，也就是说，右子树-左子树=0或1，只有这两种可能。

反过来，如果mid向上取整，自然就是左-右=0或1

无论哪种方式，折半查找判定树是平衡二叉树，而且只可能有最下面一层不满，那么树高就可以用完全二叉树的算法去算，即log（n+1）向下取整

分块查找

其实分块的最佳储存结构是索引数组+n条链表，操作系统里也会有类似结构出现（比如文件索引）

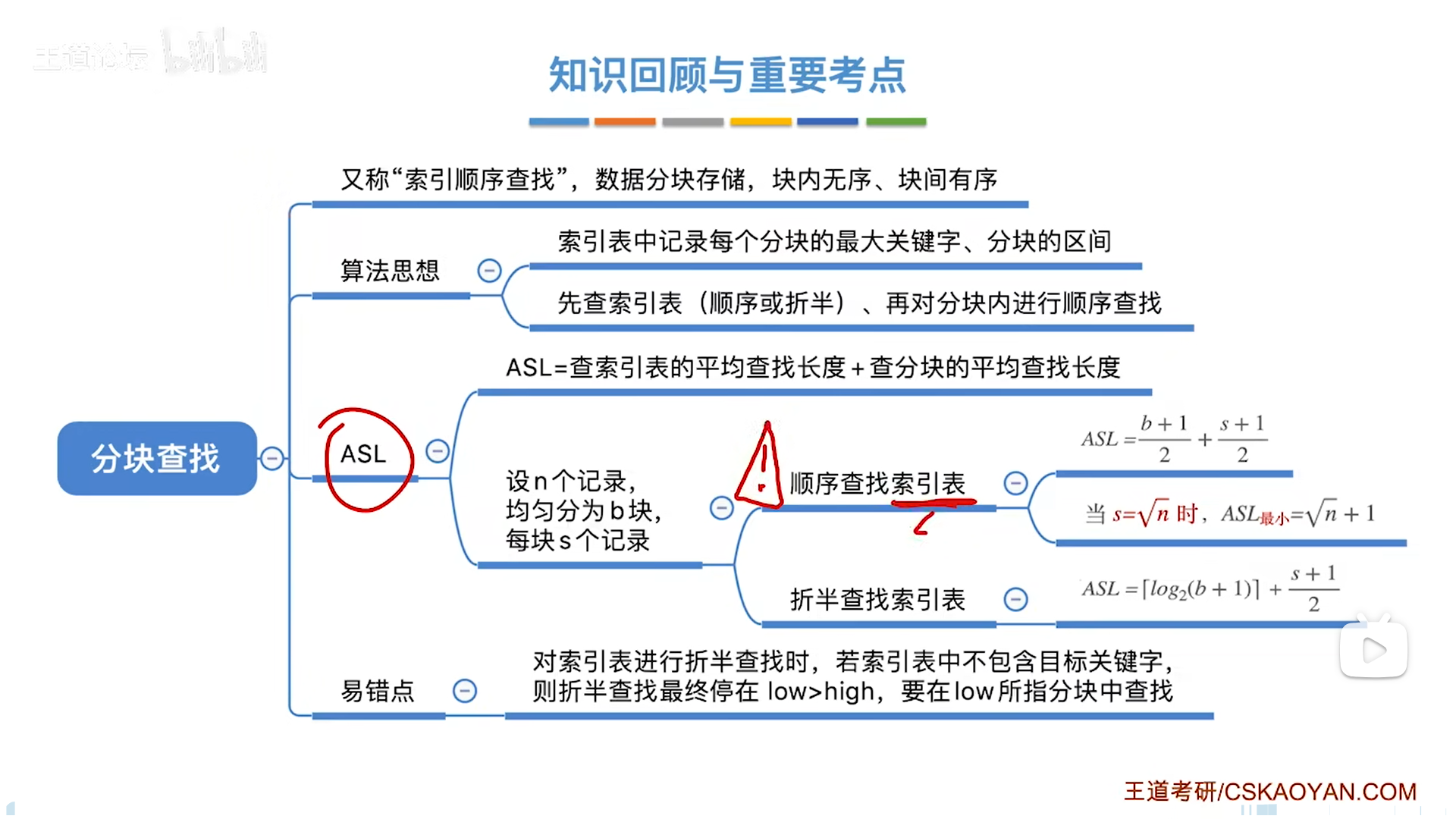
分块查找=索引+顺序，索引用来缩减范围，进而使得顺序查找次数更少

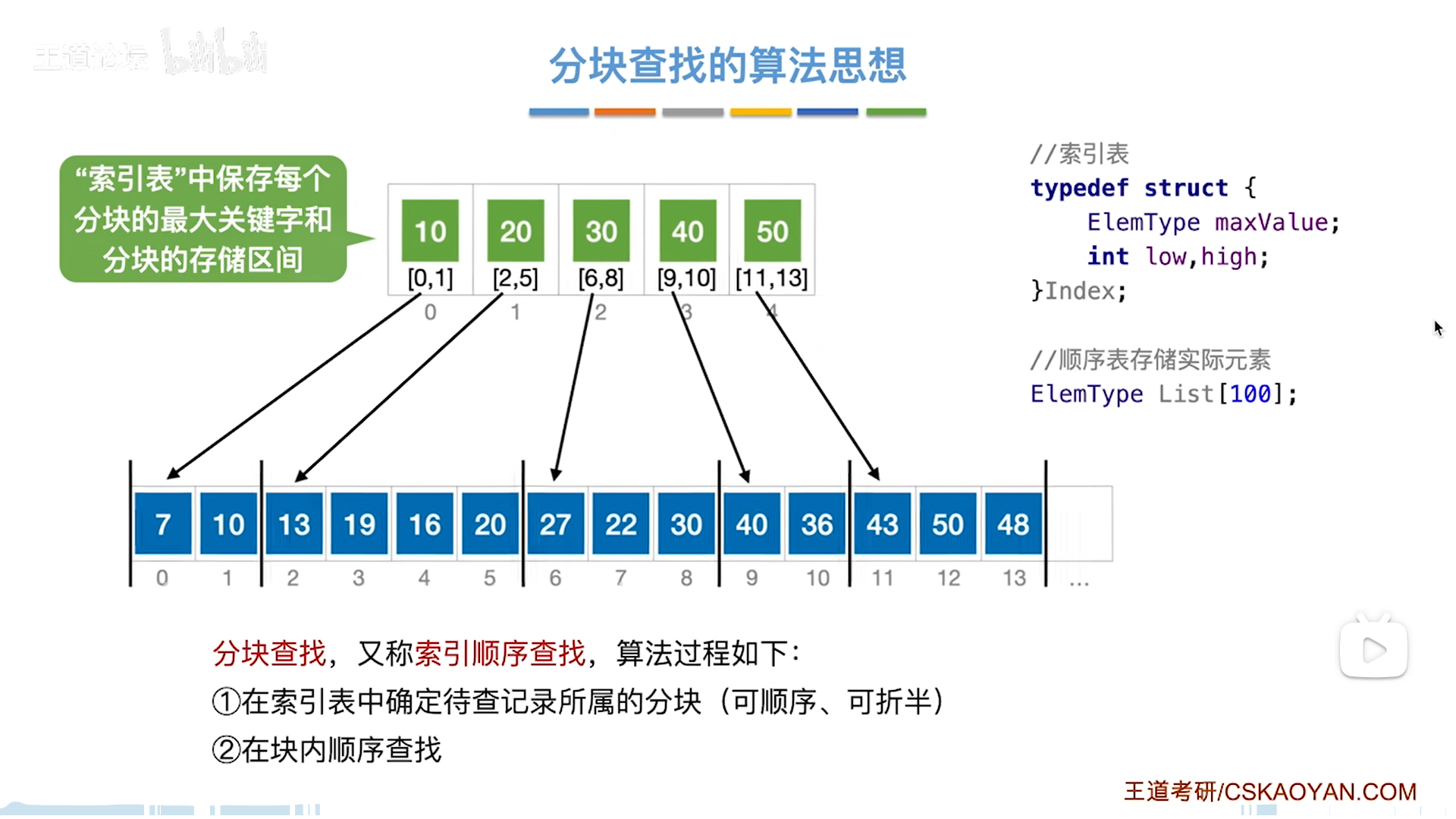
值得讨论的是查找索引的过程。

首先要明白，索引中的maxValue代表索引中最大的值（包括最大），这是后面讨论的基础：

1. mid=key，这种情况其实比较少见
2. mid≠key，则最终一定会停在low上
   • 最终high在左，low在右
   • 因为low左边都是小于目标key的，根据前面maxValue的意义，索引的值都小于key了，那必然不存在，所以low左边是不可能的（太小），而low右边又太大了，那么最后就会卡在low上
   • 假如low越界，代表所有索引对应的块都不可能存在目标key
     

对于每一个节点，其SL=索引查找次数+顺序查找次数

需要注意折半情况下的索引查找次数，分析起来比较复杂，假如key≠mid，那么最后就要反复调整直到high<low的时候，这才是真正的索引次数。

因为SL有两部分，而且相关联，所以算ASL比较麻烦，为了便于分析，直接把数组等分，那么这两部分的关联性就打破了，可以分别计算ASL1和ASL2，最后相加。

具体分析，顺序情况下，n=sb，因此把b=n/s带进去ASL就可以得到一个式子，进而求得极限情况的ASL

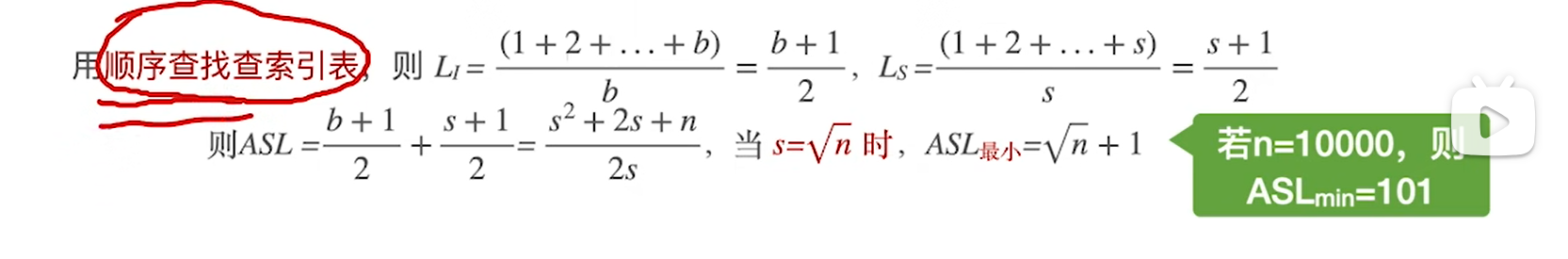
其实这才是最完美的索引顺序结构。

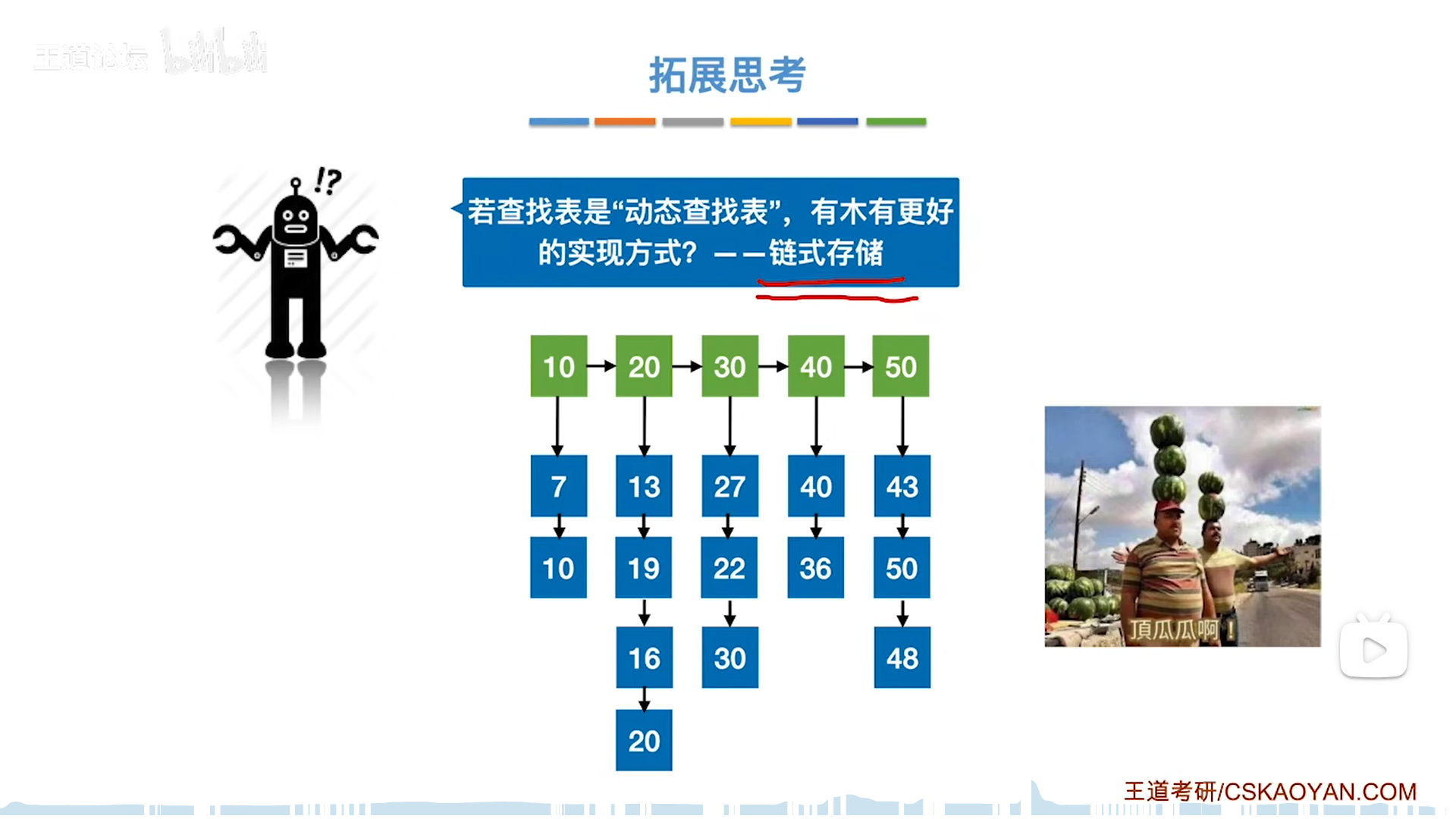
树查找

二叉排序树可以说是，带有伸缩功能的顺序数组，只是说不平衡会导致其效率退化
而进一步的AVL树，弥补了不平衡的问题，在保证伸缩性的前提下，最大化逼近数组的效率
可以说是比较完美的结构了。

二叉排序树（BST）

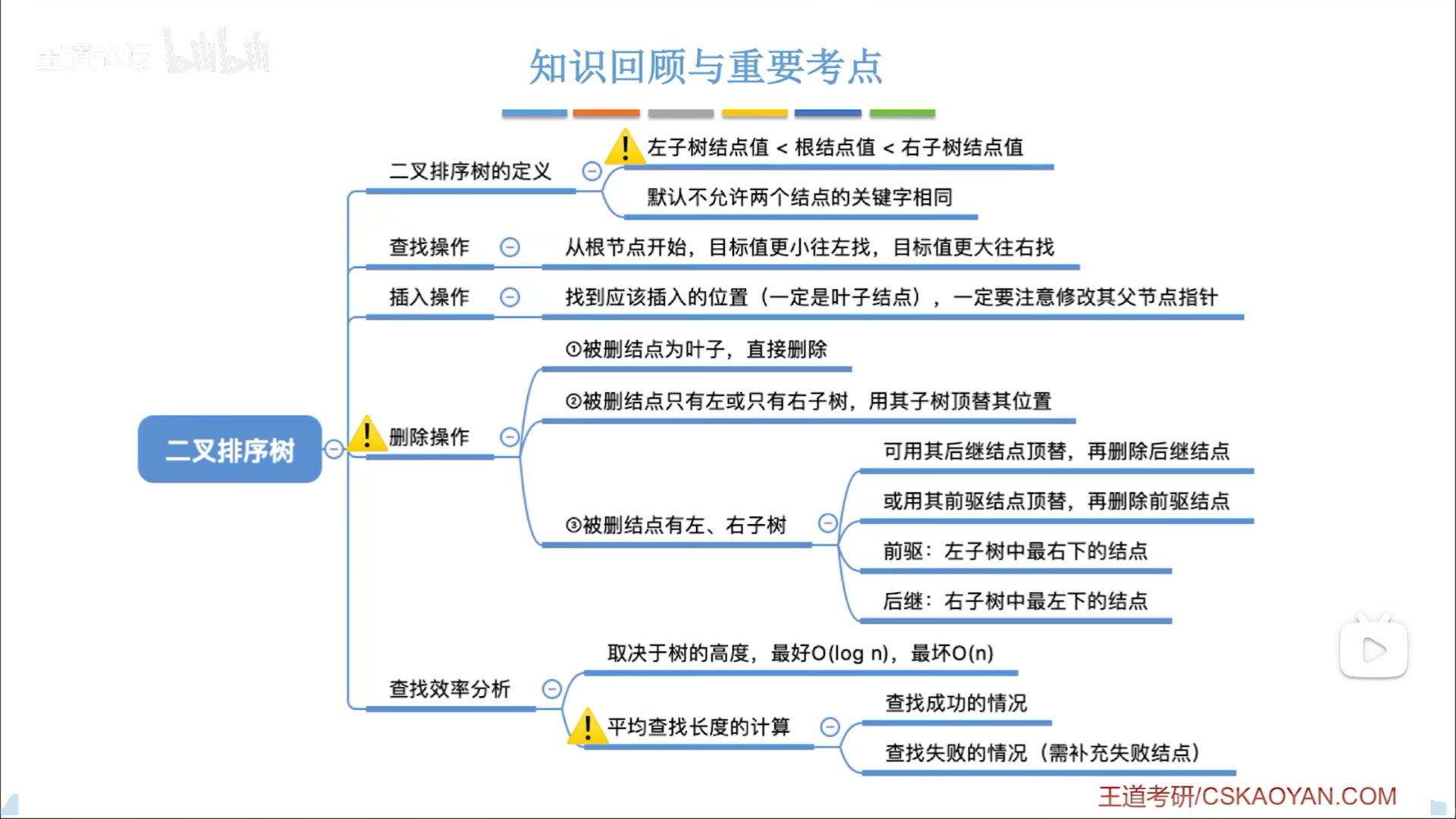
递归和循环的思路一样：

1. 退出条件：空，或者匹配到
2. 否则就查左/右子树

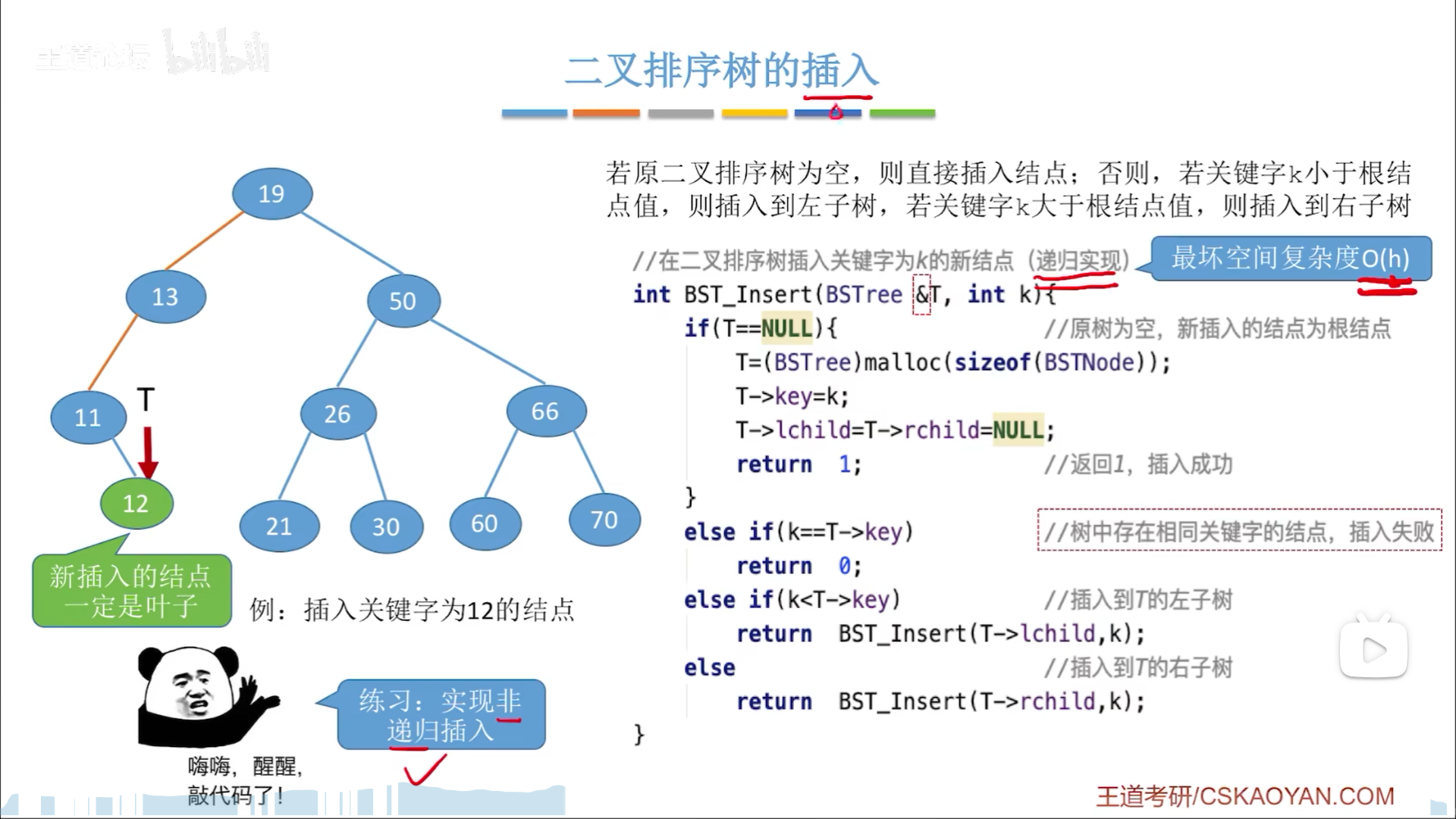
插入，就是要找到插入点位：

1. 有一样的，失败
2. 没有一样的，生成新节点，令父节点链域指向该节点。
   • 父节点指针从何而来？需要注意BSTree &T，也就是说，在最后T==0的时候，这个T不仅仅是空指针，其本身还是父节点的孩子链域，因此我们直接把T指向新节点就可以了，在第一步就完成了。
   • 记得初始化左右孩子为NULL

有了插入后，给定一个T=NULL的初始链域，就可以反复插入，形成二叉树。

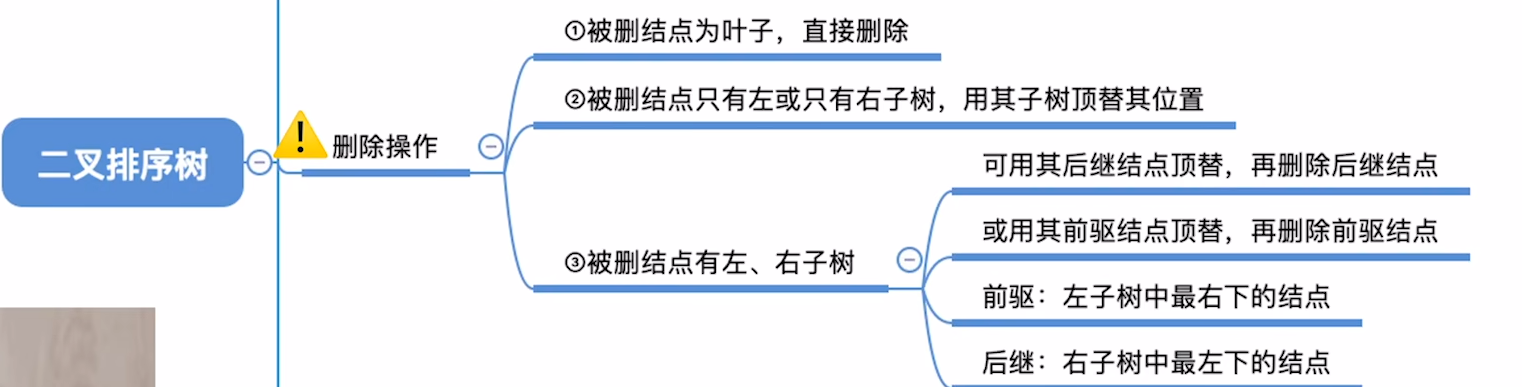
删除节点，这个涉及到树结构的重构，比较复杂：

1. 叶子结点
2. 只有单边孩子
3. 有双边孩子，按照中序序列，上层是左根右，展开后变为（左根右）根（左根右），删去根后有两种顶替思路
   • 以右子树最左边的节点顶替根（大中最小），那么拆掉的这个节点又该怎么补呢？恰好最左边的节点，一定不可能有左子树，这就划归到了2情况
   • 左侧情况反过来就行
     

查找效率用ASL评估，这俩在查找中是等价的。

给定具体的一个例子，成功的ASL则要去计算n个成功节点的加权，而失败则要补n+1个失败节点，再加权

下图表示，二叉树查找的平均效率与其高度成正比，那么理想情况是把高度压制成平衡二叉树，这就是后面的内容了。

平衡二叉树（AVL）的插入

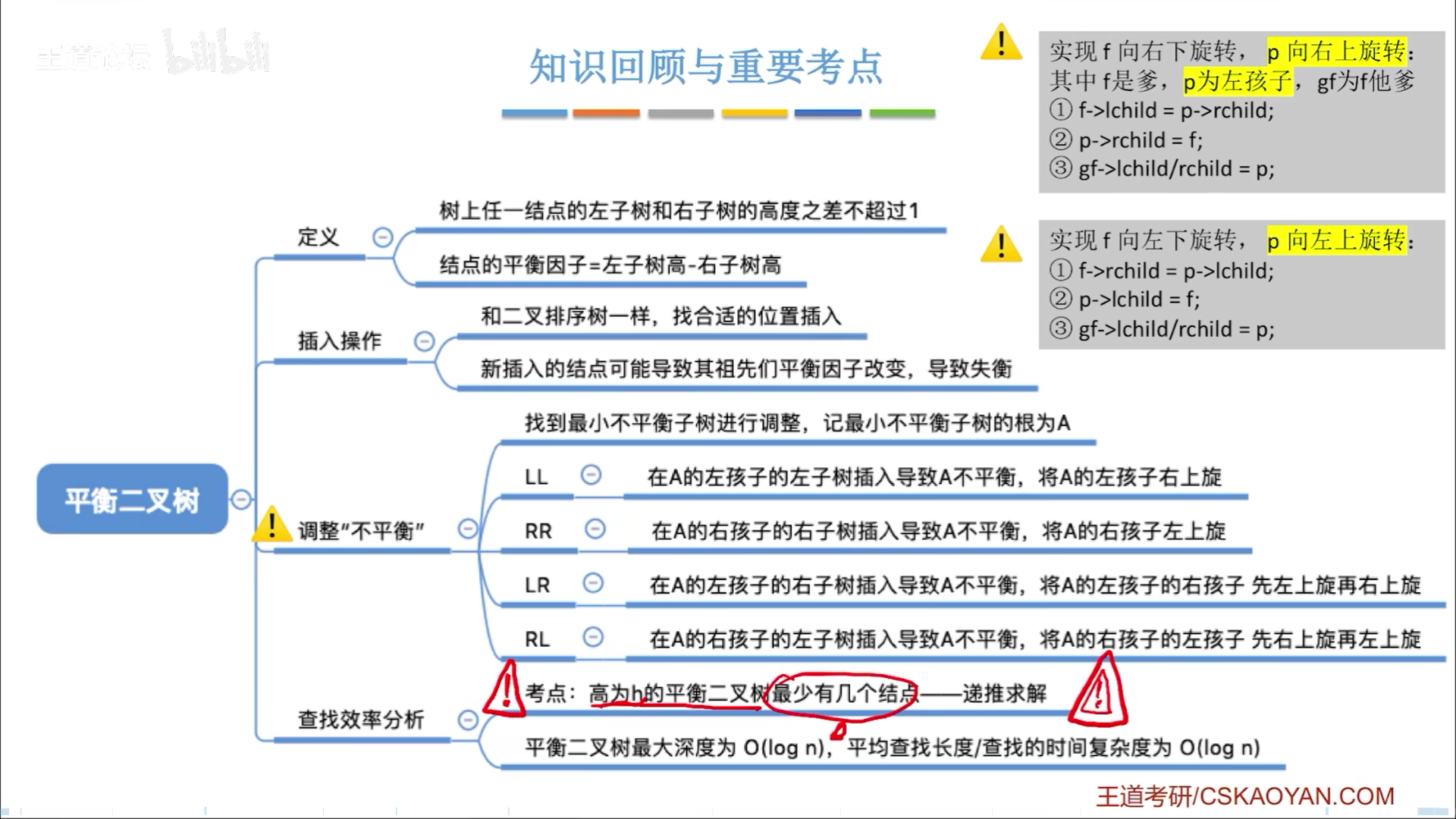
平衡化

平衡二叉树，任一节点的平衡因子（左-右）都只可能是-1,0，1，如果添加节点导致破坏平衡性，就要找到最小不平衡树，进行平衡化修正

以最小不平衡树根节点为A，则不平衡无非就是四种情况，LL，LR，RL，RR，这四种情况的记忆方法如下：

1. 第一个字母代表A的左右子树
2. 第二个字母代表子树的左右孩子

因此LL就是左子树左孩子插入，导致不平衡，到时候自己画图就好。

首先要说明，三个子树都是H高度，这个是铁定的，否则插入就不会破坏平衡性。

LL和RR比较简单，本质在于让B当根节点，因此转一下就行

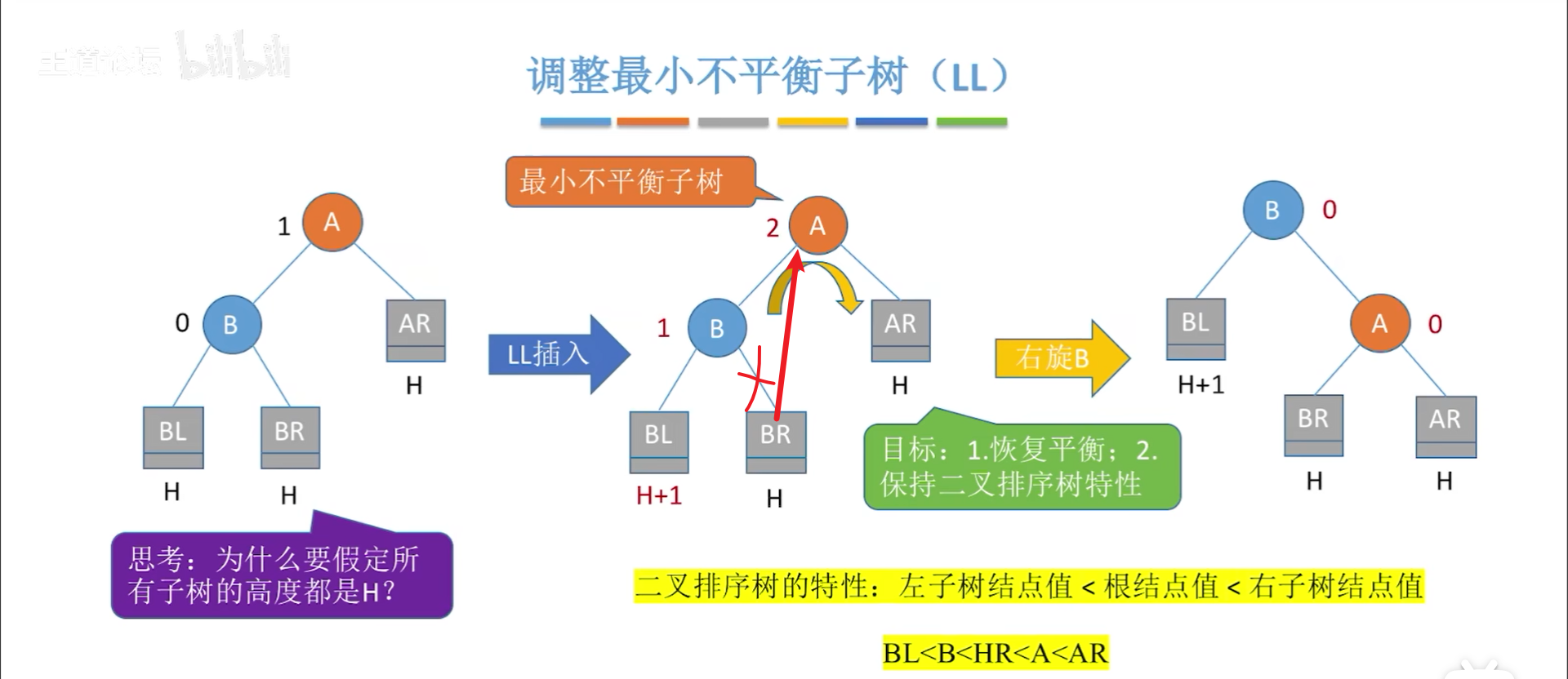
看下操作，实际上是要让B当根，A当孩子，因此分三步，写旋转代码要按这三个步骤来：

1. 替换A的左孩子，此时A成为一颗可以随意挪动的树
2. 让A成为B的孩子
3. 让B成为根节点

LR和RL复杂一些，对于LR，具体还要把L子树的R孩子（高度为H+1）继续展开，以便于分析，但是实际上，这两种情况是一样的，因此假定是下图情况。

但是实际上本质不变，最终的目标是让C当根节点，BA分别为左右，那么C就要转两下，先和B在和A，这样C就可以变成根节点，两次旋转沿用前面的思路即可。

RL也是如此，最终要让C当根节点。

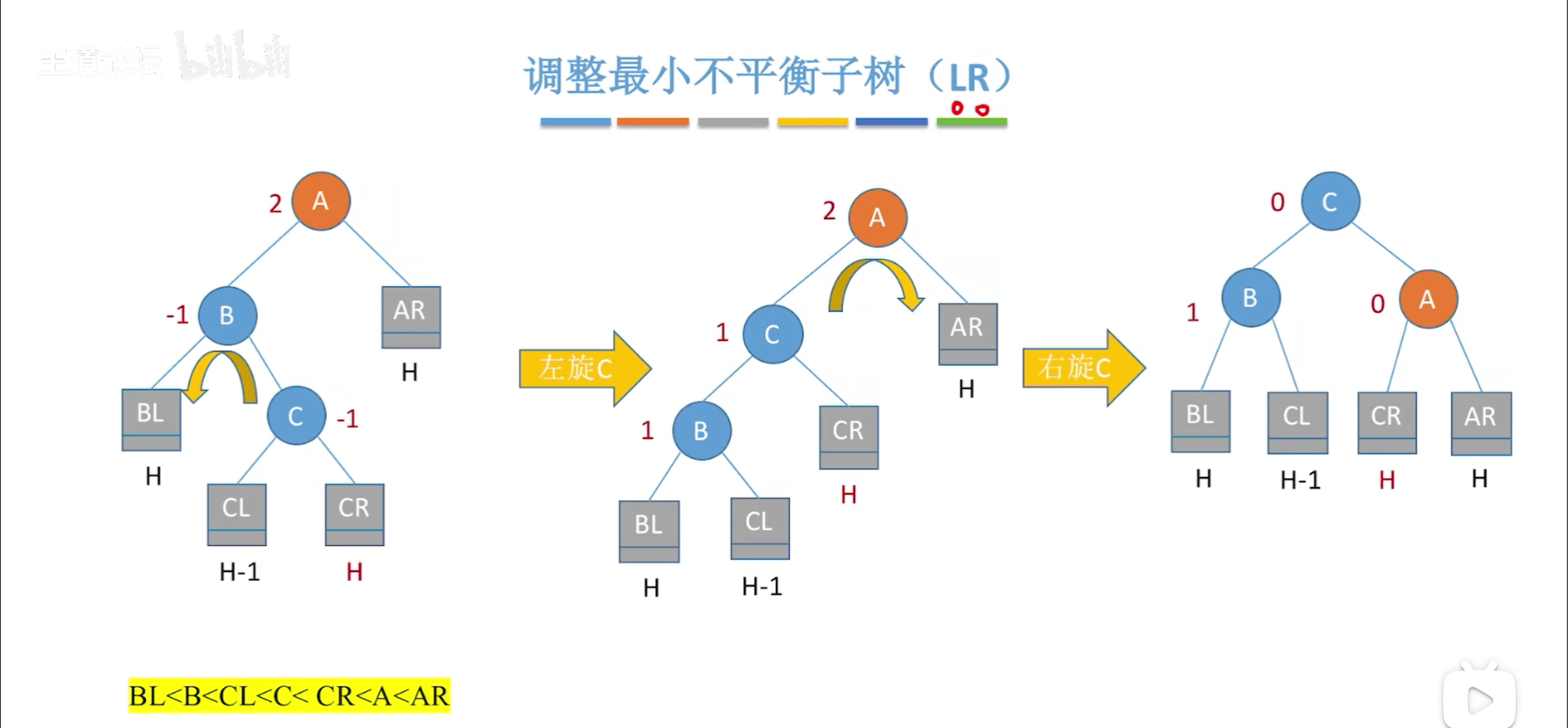
最后再整体总结一下，你会发现4类情况，最小不平衡子树本来都是H+2高度，然后插入新节点变成H+3，破坏平衡性，调整以后重归H+2，同时平衡性保持住了

之所以只调整最小不平衡树就可以保证整体平衡性，是因为这一通调整将多出来的高度抹平了，更上面的节点的平衡因子自然就退回到平衡状态了。

我们把眼光落实在做题上：你要盯一眼，从下往上找到第一个不平衡的节点，代表最小不平衡树的根节点，然后回忆4种情况，标上ABC，剩下步骤就很简单了，如此就秒杀了。

复杂度分析

无论是插入还是删除，费时间的其实还是查找目标位置，说白了ASL和查找是一样的，调平衡度不影响。

再有就是复杂度分析，ASL=层数，即O（h）效率，关键在于如何通过节点数量n计算h的上界（或者通过h计算n的下界）

这是个数学问题，根本在于AVL的特性，即平衡因子最多为1，那么极限情况就是高度为h的树，一颗子树高度为h-1，另一颗为h-2，因此这颗树的节点数$n_h=n_{h-1}+nh-2+1$=左子树+右子树+根

考虑初始情况，高度为012，最少节点也是012，按照递推就可以计算出任何高度的节点数下界。
反过来，已知n，就可以知道h上界
最后算ASL，经过一通推导，结果就是O（logN）

平衡二叉树的删除

第一步是按照二叉排序树删除，这一步本身就挺麻烦

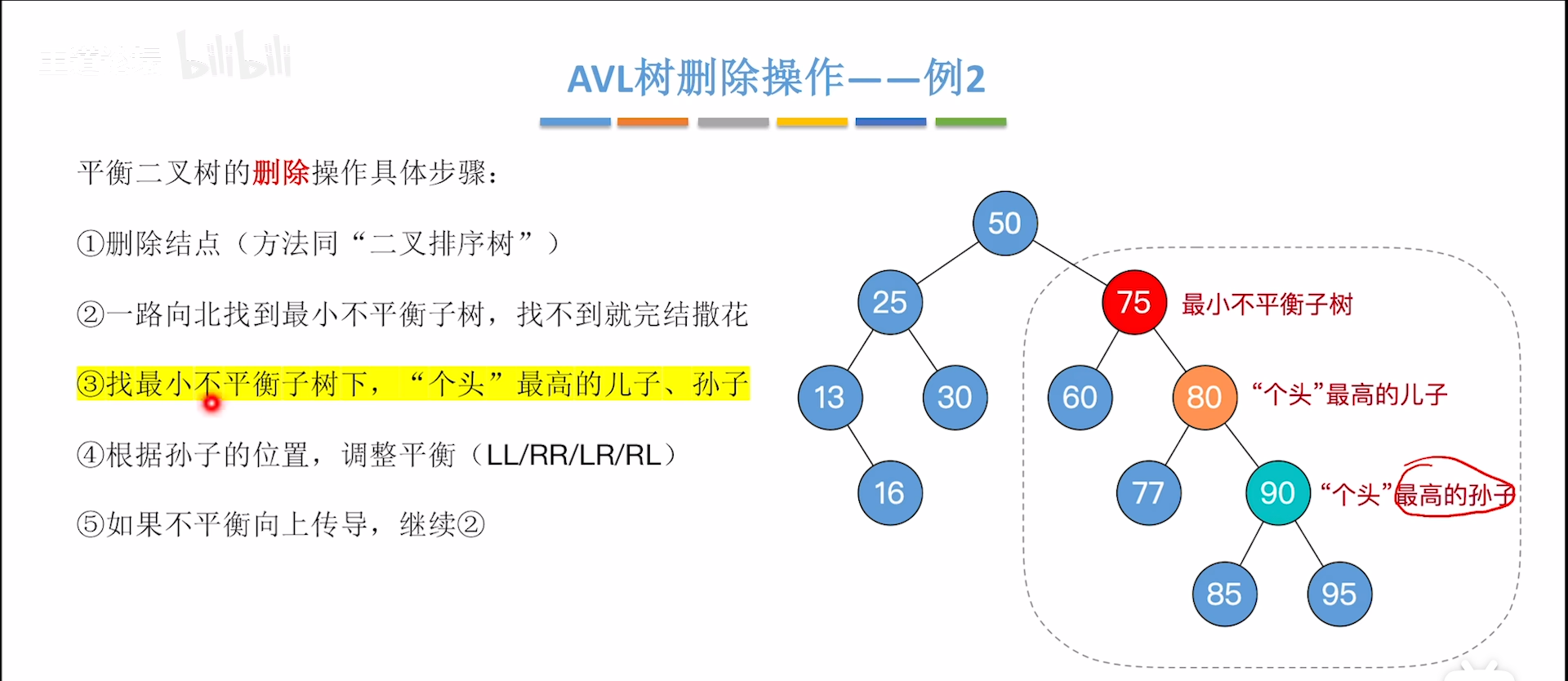
先看一个简单的例子，熟悉流程

1. 从删去点向上找，找到第一个不平衡节点，这就是最小不平衡树的根
2. 从根开始，找个头最高的儿子和孙子，其实就是从上往下，找到不平衡的传导链条
3. 判断4类不平衡情况，进行旋转
   • 这一步可以使得不平衡部分的H减小1，这样可能会导致树的另一侧过高失衡，要二次调整，回到1步开始

接下来举一个需要二次平衡的例子，下图进行第一次平衡后，右子树高度减一，导致左子树太高。

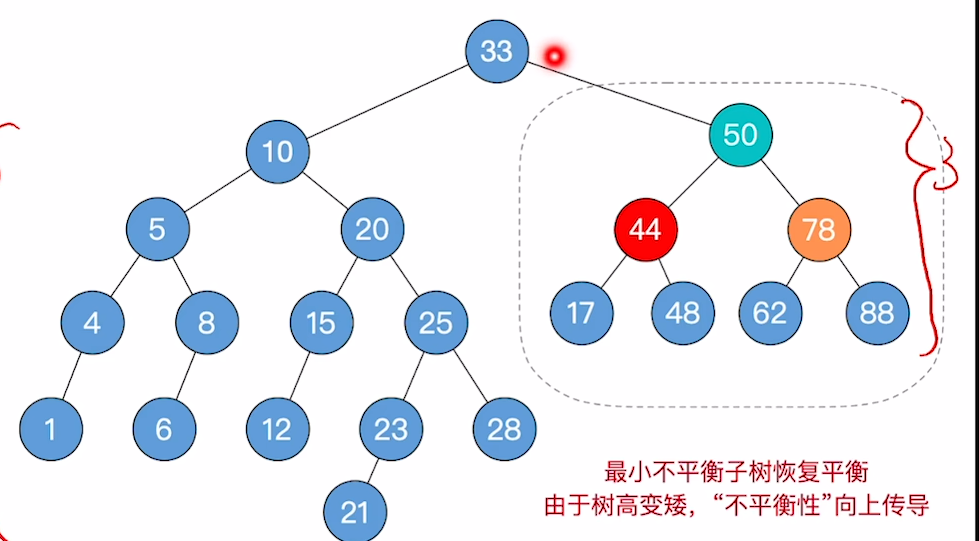
跳回到1步：

1. 从调整点位开始向上找，找到第一个不平衡点，即33
2. 然后从根节点开始向下找不平衡链条，为33-10-20
3. 进行翻转，即可平衡

有没有可能出现第三次不平衡？有可能，因为我们这次找到根恰好也是整个树的根，因此一步到位，假设我们找到的根上面还有东西，那么这一层降低高度后还有可能导致另一侧失衡，总之是一定要向上找是否失衡

考试中可能出现的最极限的情况是，删除的节点同时有左右孩子，那么这个时候就有两种删除方案。
后面仍然按照我们的流程来进行调整

但是这其实就有歧义了，408不太可能出这种，最后提一嘴，复杂度同查找，O（logN）

红黑树

红黑树的定义和性质

虽说AVL的复杂度是logN，但是实际上，每次找最小不平衡树比较费时间，实际消耗时间会有一个常数级别的放大，如果要频繁改变结构，就比较慢，红黑树应运而生。

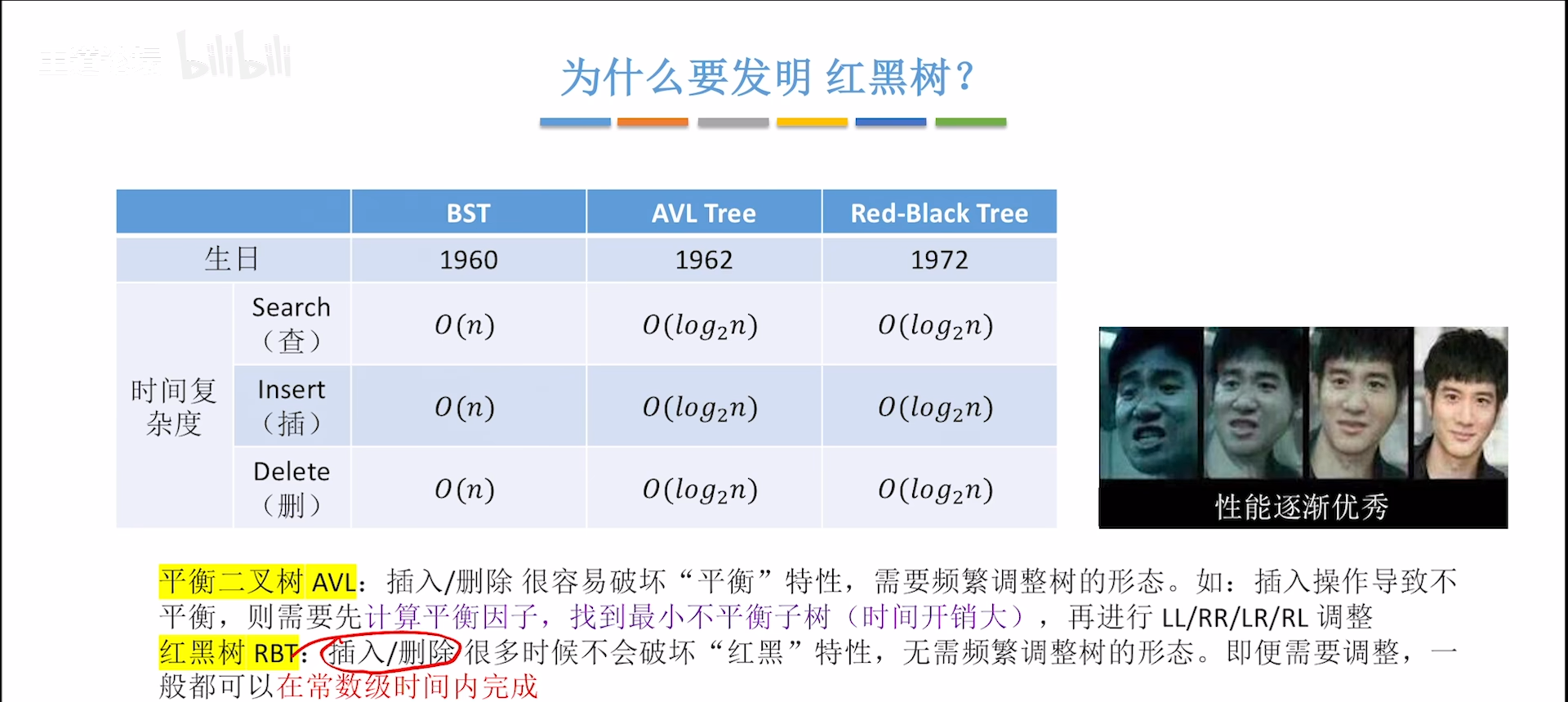
首先明白，红黑树是从BST，AVL一脉相承过来的，所以本身也具有BST性质：左＜根＜右
或者说，AVL和红黑树都是BST的改进，AVL和红黑树严格来说是并列关系，但是性能是要碾压的

红黑树相比于BST来说，有两点改变：

1. 使用三叉链表结构
2. 增加了节点的红黑特性（对标AVL的平衡因子，但是有所不同）

红黑树定义

多出来的两个信息，可以为操作带来诸多方便，理解一下下面的规律：

1. 左根右。这告诉我们红黑树的本质还是BST
2. 根叶黑。根节点和叶节点都是黑色的
   • 叶节点并不是我们传统意义上的叶节点，而是代表（外部，NULL，失败），这三个说法是等同的，也就是我们之前判定树计算失败ASL时补上的节点。
   • 与叶节点对应的就是内部节点，就是有具体意义的节点，可以成功的节点。
3. 不红红。不存在相邻的红节点
   • 这是对红节点的限制，但是黑节点无所谓，可以相邻
4. 黑路同。任意节点（不一定只是根节点）到任一叶节点的通路上，路过的黑节点数量相同
   • 这是对黑节点的限制，同理红节点无所谓

一个基本功就是判断红黑树是否符合定义，大致思路如下：

1. 根叶黑。先看根节点和叶节点
2. 不红红。扫一眼看看有没有红节点相邻
3. 黑路同。这个就比较复杂了，你在看一眼黑色聚集的比较多的地方，那些地方极有可能会出现黑色路径过长，黑节点太多的问题
4. 左根右。这个也容易埋坑，你要知道红黑树首先是一颗BST，所以如果出题很阴，会出在这里。

下面这道题很阴，看哪个7，好在这种情况一般是出现在前三条都失效的时候，此时选择题里估计最多剩俩选项，硬着头皮细心对比就行

红黑树性质

性质清单：

1. 黑高定义，h
2. 给定h，内部节点下界
3. 给定h，内部节点上界（红节点上界）
4. 最长路径最多是最短路径的两倍
5. 给定n，设H为总高度（非黑高），则高度上界$H\le 2lo{g}_2(n+1)$

前面铺垫一大堆，都是规定，通过这些复杂的规定，可以产生很多有趣的性质，这才是红黑树高效率的开始。

首先从“黑路同”里衍生一个概念：

黑高，即从这个节点开始，走到任意一个叶节点经过的黑节点个数（不包括自己）
根据黑路同逻辑，一个节点的黑高一定是一个具体的值，从一个特定节点开始，无论是从那条路走，黑高都是一致的，因此用统一的值描述。

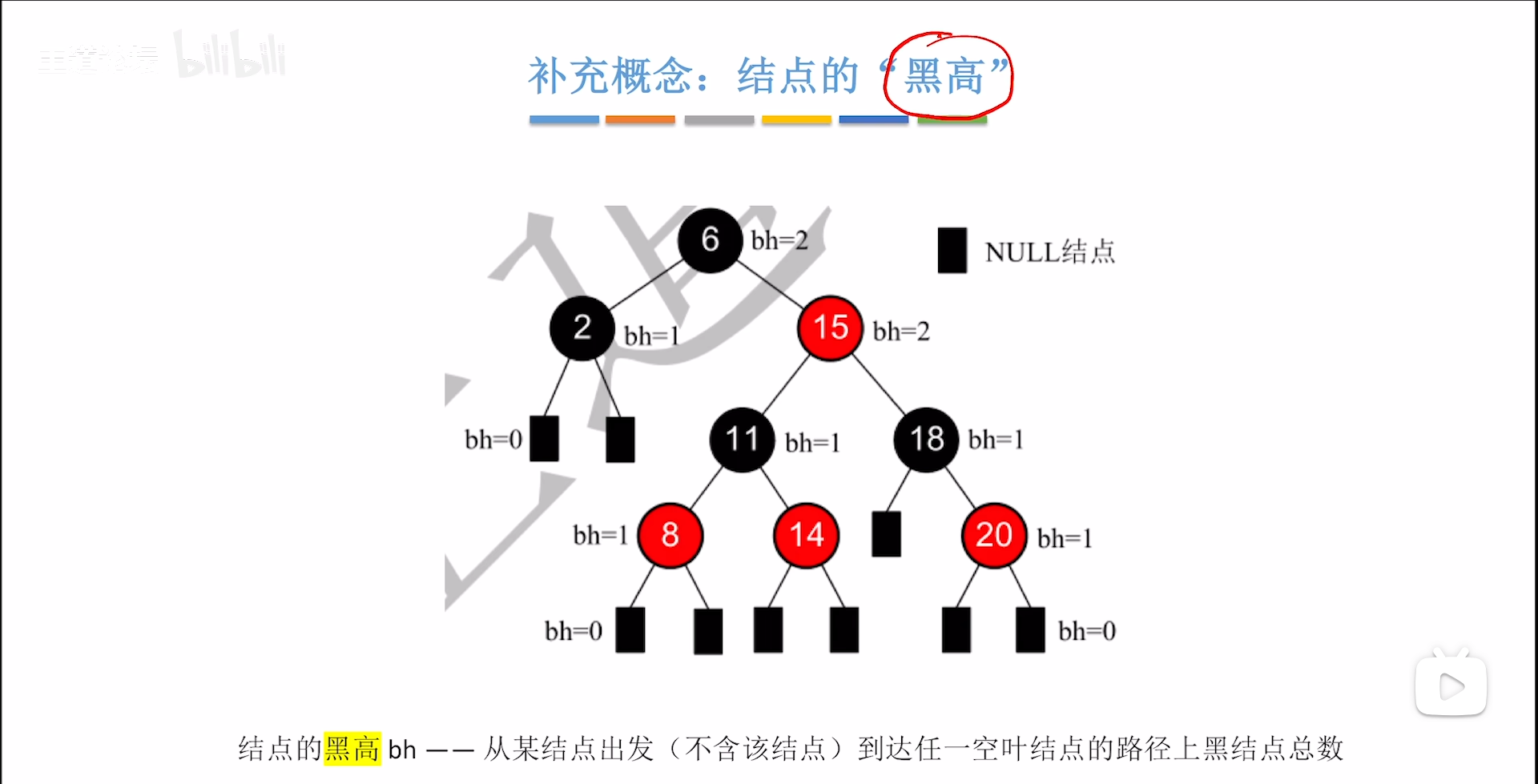
其实我们更深地考虑一下，黑路同这个特性很好玩，如果不考虑红节点的话，纯黑情况下一定是满二叉树，黑高就是内部节点的层数，因此黑高为h的红黑树，内部节点至少是$2^h-1$

而红黑树是什么东西呢？其实就是在一个满二叉黑树之间，尽可能塞入不重复的红节点，那么给定黑高为h，极限情况下，可以塞入$2^{h+1}-2$个红节点，

这个的计算如下图，给定h为黑高，算上最顶上的那个×，总共可以塞h+1层红节点，即$2^{h+1}-1$个，然后你再去掉顶部×这个不能加的节点，因此就是-2

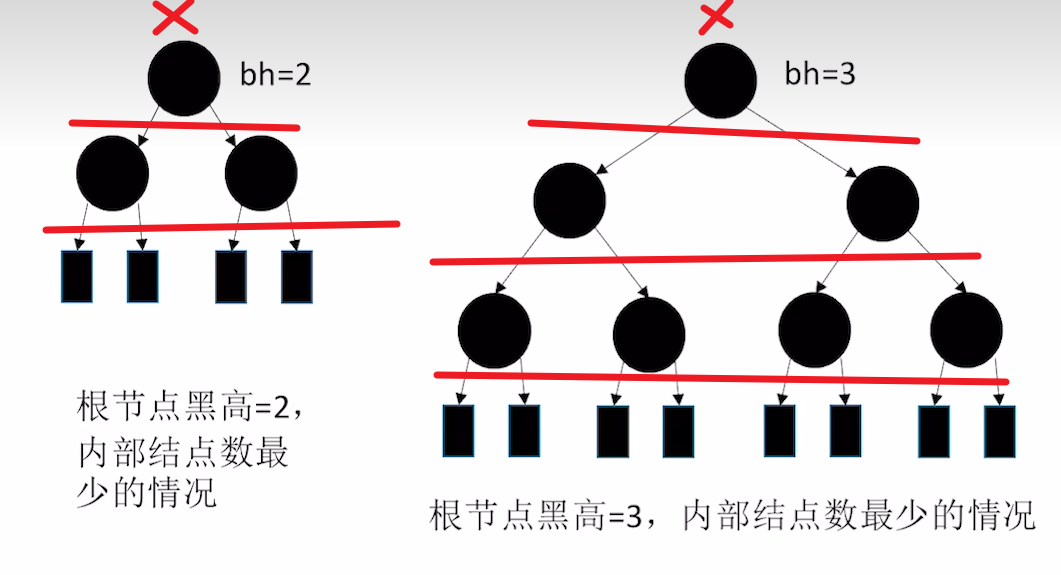
其次再论两个性质：

1. 根节点到叶节点的极限路径长，最多为两倍关系
   • 最短路径为纯黑
   • 最长路径为从黑（根节点）开始：红-黑-红-黑，实际上路径就是一红一黑，插入尽可能多的红节点，也就是最短路径的两倍
2. 给定内部节点N，则极限高度为2log（N+1），因此查找操作的ASL和AVL一致
   

红黑树的插入

如何构建一颗红黑树？
或者说如何在插入的时候保持红黑特性？
这就是本章研究的问题

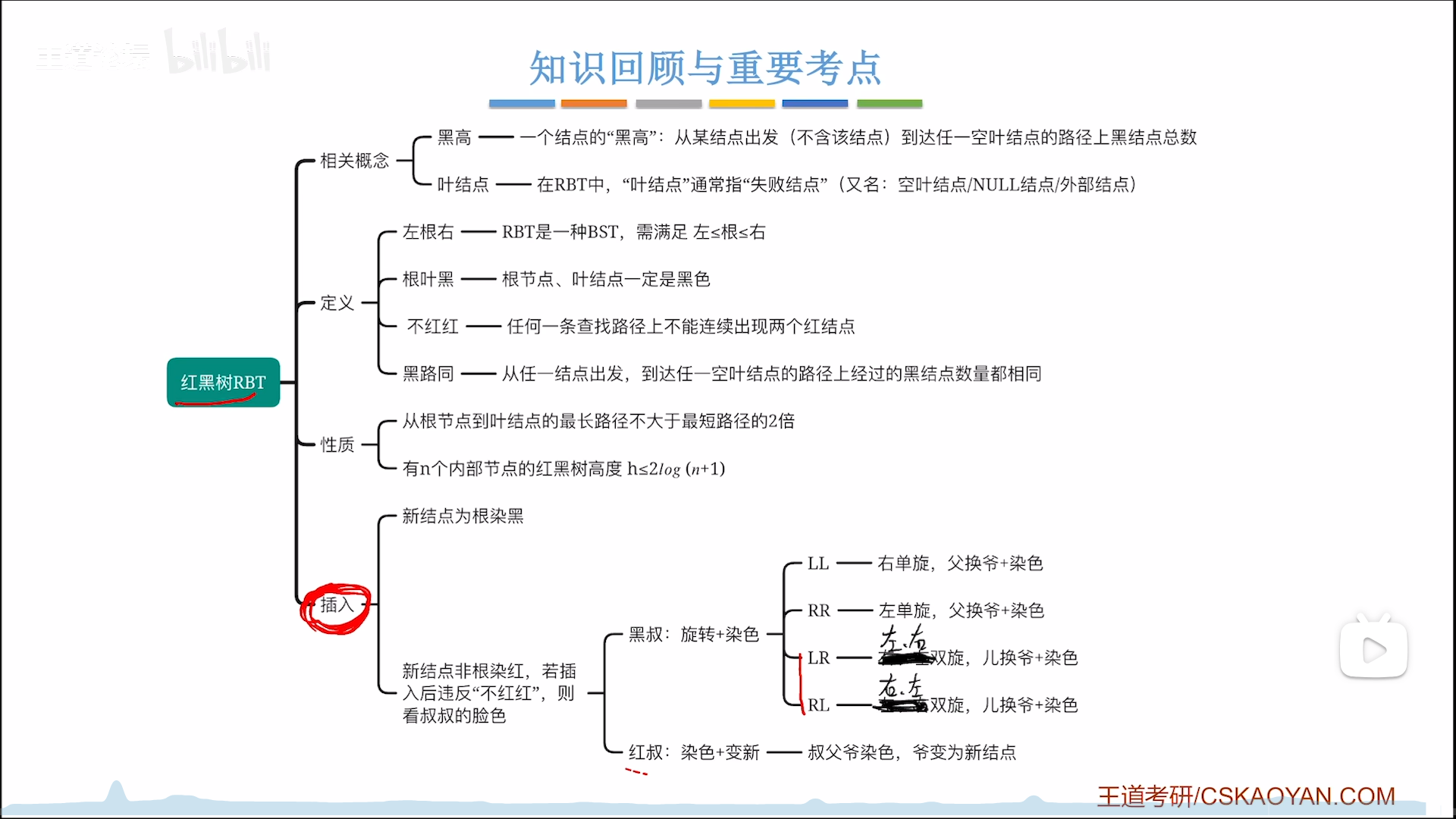
插入一个节点操作如下：

1. 根节点染黑，根叶黑
2. 非根节点染红，能够保证黑路同
   • 可能不平衡，1,2条可以保证根叶黑，黑路同，而找节点的过程也满足BST特性，因此唯一可能不满足定义的地方就是红节点连续，而且不平衡只可能在非根节点时候发生
   • 因此不平衡=红节点连续，调整要看叔
   • 叔黑，旋转+染色
     • 首先要找到旋转的极大不平衡根节点，从下面插入的儿往上，上层为父，上上层为爷，爷其实就对应AVL里面极大不平衡树的根节点
     • 对于LL，RR型，父爷换，之后令交换的两个节点反色
     • 对于LR，RL型，把儿换到爷位，之后令交换的两个节点（爷儿）反色，父节点不反色
   • 叔红，反色+判新（不用调整结构）
     • 反色部分为父叔爷，其实就是把上面两层反色
     • 判新，指把爷当做新节点，跳到第1步

下面这个例子是：不平衡+黑叔+LL/RR型，先单旋再反色

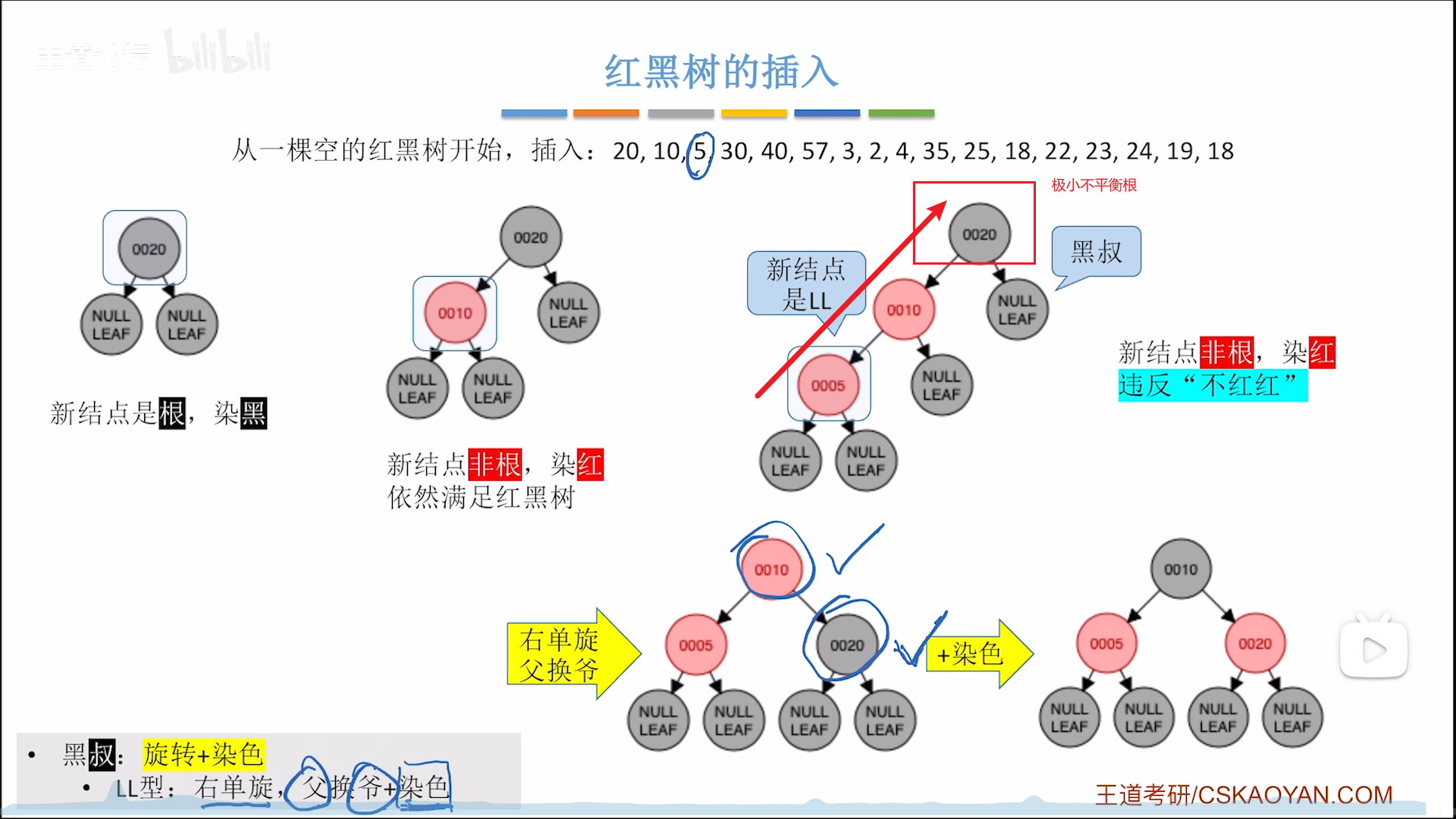
下面这个例子是：不平衡+红叔，则反色上两层

然后以爷为新节点，再判断一轮，此时为：根，染黑

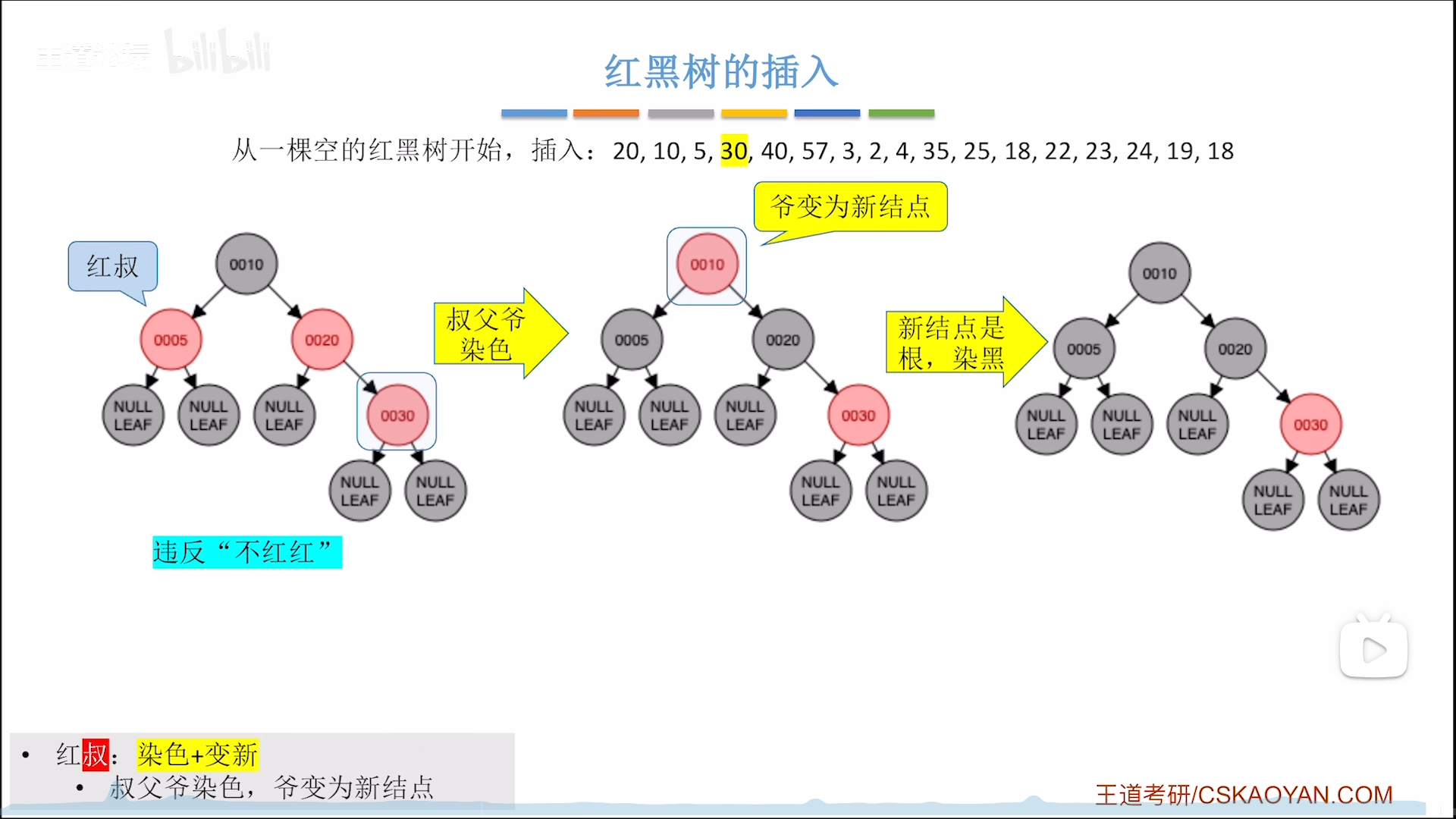
当红黑树逐渐变大，你会发现红黑树有一个有趣的特性，就是大部分情况下是不需要调整的（其实AVL和红黑树的最终目标都是平衡，那么AVL其实也差不了太多，关键在于AVL需要去向上找最大不平衡根，而红黑树的爷就是最大不平衡根，寻根效率更高，这才是红黑树碾压AVL的本质）

下图是一种连锁反应，这种连锁反应只可能在不平衡+红叔时发生，因为爷要当做新节点，跳回1，会触发连锁反应。

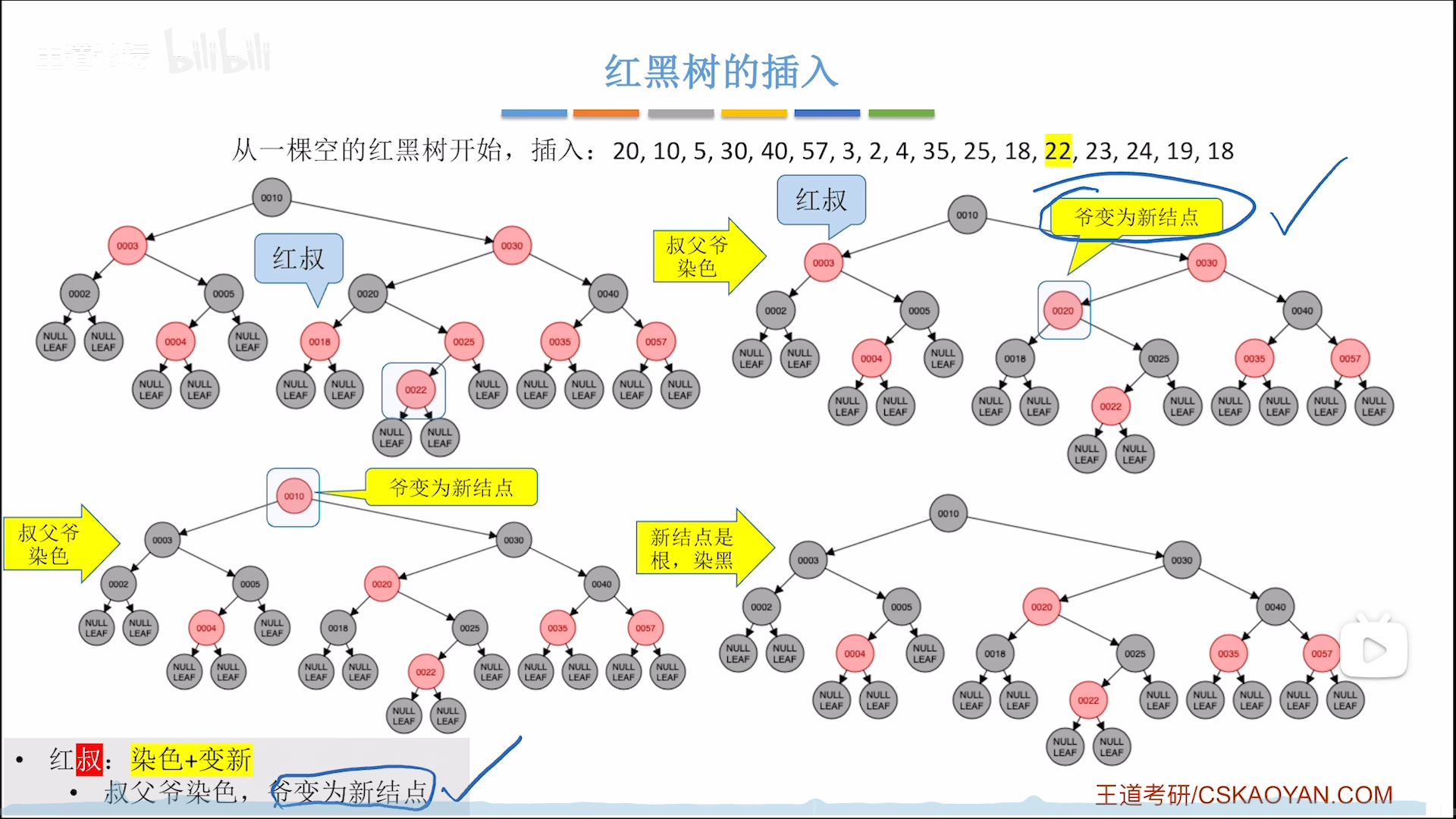
再来看一个LR的例子：不平衡+黑叔+LR=旋转+反色

1. 先旋转两下
2. 然后进行反色，注意只反爷儿，父不管

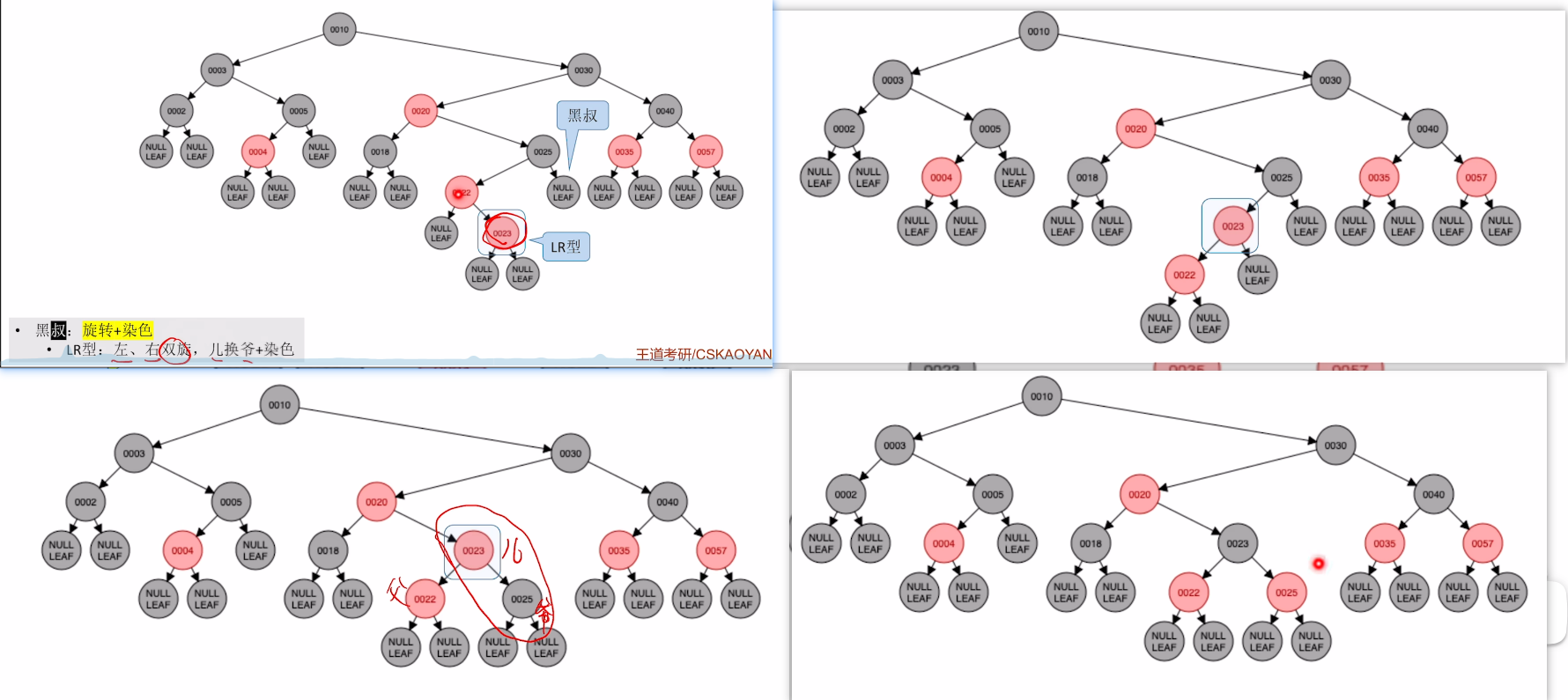
红黑树的删除

虽然视频没说，但是我脑子里已经有一个大致的思路了，因为删除的思路和插入其实一样。

首先按照BST删除思路，进行删除
之后必然面对结构破坏的问题，就要进行调整，我们可以利用一个逆向思维，假设自己是在进行插入操作，就当他是插入操作导致的结构破坏，然后我们用插入的思路来调整结构。

而这个思路的关键在于，你要明确儿子节点到底是哪个，又或者干脆就利用红黑树定义去修改颜色和位置

到时候凭感觉就行了，真考出来咱们就大难临头各自飞，我自己也不知道（乐）

B树

B树基础

B树插入和删除

B+树

散列查找