爆火的Swin Transformer到底是什么

文章目录

一、名称解读
二、ViT回顾
三、Swin Transformer vs ViT
四、Swin Transformer结构
- 4.1 Patch Merging模块
- 4.2 相对位置编码
- 4.3 shifted window
五总结

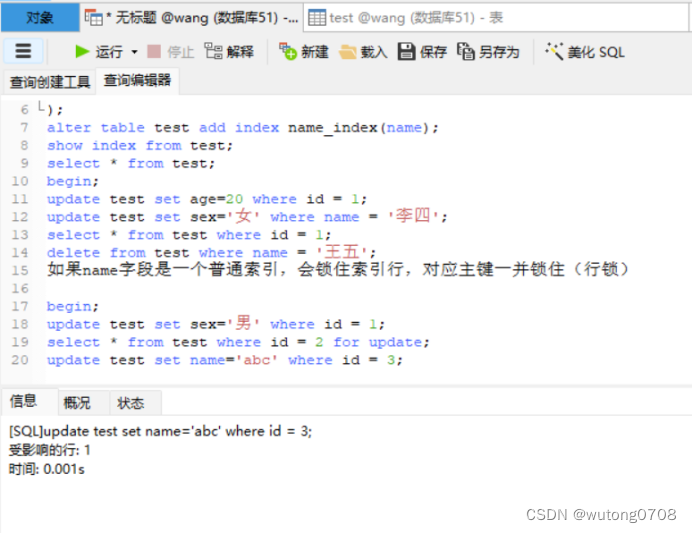
爆火的Swin Transformer究竟是个啥？今天本篇文章系统讲解下Swin t 结构、优点、位置编码、移位窗口shifted window，并附上部分代码的解释

论文名称：《Swin Transformer:Hierarchical Vision Transformer using Shifted Windows》，简称Swin Transformer、Swin T
论文下载：https://arxiv.org/pdf/2103.14030.pdf
代码地址：https://github.com/microsoft/Swin-Transformer

一、名称解读

其实论文名字就很好的点出了Swin Transformer的特点，Swin是指Shifted window，使用移位窗口的多层级视觉Transformer，重点在于Hierarchical多层和Shifted Windows移位窗口

二、ViT回顾

ViT是2020年Google团队提出的将Transformer应用在图像分类的模型，虽然不是第一篇将transformer应用在视觉任务的论文，但是因为其模型“简单”且效果好，可扩展性强（scalable，模型越大效果越好），成为了transformer在CV领域应用的里程碑著作。

图一 ViT结构

ViT将二维图片切分为patch，然后序列输入，经过一个线性层（全连接），再加上position，对应图片是左边的输入Patch+Position embedding，在输入的下面还有一行小字Extralearnable [class] embedding，它是特殊字符CLS，借鉴Bert，根据它的输出做分类的判断（transformer的输入和输出维度相同，但是只要一个分类结果，所以增加了一个cls token）。然后经过一个标准的Transformer Encoder和MLP头，输出结果。

三、Swin Transformer vs ViT

Transformer应用到图像领域主要有两大挑战：

视觉实体变化大，在不同场景下视觉Transformer性能未必很好
图像分辨率高，像素点多，Transformer基于全局自注意力的计算导致计算量较大

遇到高分辨率的图像，采用ViT处理会产生极大的计算复杂。而Swin Transformer的复杂度会比ViT低，主要通过下面两点降低计算复杂度：
（1）分层特征图
（2）局部窗口计算注意力

图二

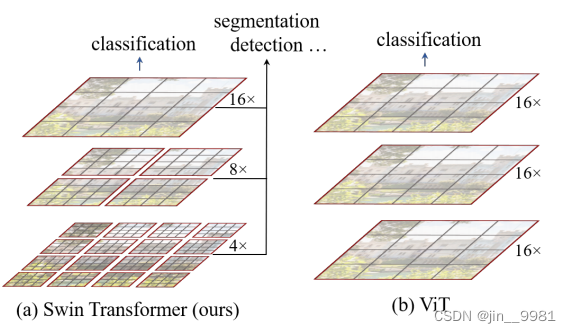
(a) 图表示Swin Transformer 通过合并更深层的图像块（以灰色显示）来构建分层特征图，并且由于仅在每个局部窗口内计算自注意力，因此对输入图像大小具有线性计算复杂度（红色）。
(b) 图是ViT生成单个低分辨率的特征图，并且由于全局自注意力的计算，输入图像大小具有二次方计算复杂度。

四、Swin Transformer结构

图三 Swin Transformer结构

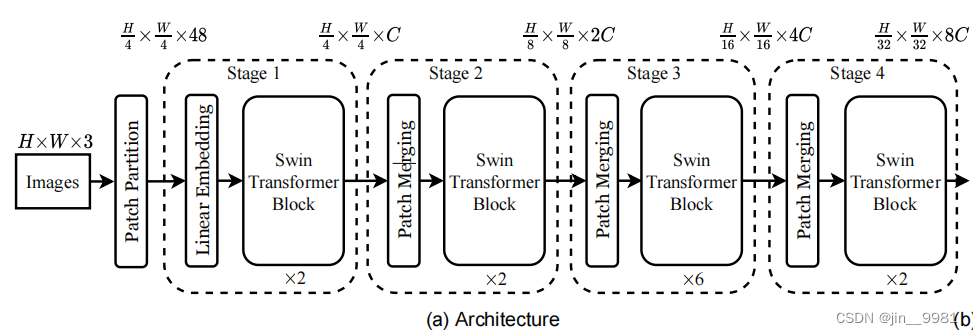
Swin Transformer的结构还是比较简洁的，它的输入和ViT类似，也是将图片切patch序列输入。用4x4的大小切分成patch，则每个patch是4x4x3=48，输出是 $\frac{H}{4} \times \frac{W}{4} \times 48$ 。在输入阶段，位置编码用了绝对位置编码，可以加也可以不加，作者代码中可通过self.ape参数进行选择。输入的二维图片切分patch，是通过卷积实现，将224x224x3的图片转换为56x56x96，输入部分的代码如下：

def forward(self, x):
    B, C, H, W = x.shape
    # FIXME look at relaxing size constraints
    assert H == self.img_size[0] and W == self.img_size[1], \
        f"Input image size ({H}*{W}) doesn't match model ({self.img_size[0]}*{self.img_size[1]})."

    # 1、self.proj卷积：kernel=4，stride=4，224x224x3->56x56x96，公式(w+2p-k)/s + 1
    # 2、flatten:将二维转为一维，[N, 96, 3136]
    # 3、transpose：维度转换，[N, 3136, 96]
    x = self.proj(x).flatten(2).transpose(1, 2)  # B Ph*Pw C
    if self.norm is not None:
        x = self.norm(x)
    return x

stage1：线性Embedding -> 2x Swin Transformer Block，输出 $\frac{H}{4} \times \frac{W}{4} \times C$
stage2：Patch Merging -> 2x Swin Transformer Block，输出 $\frac{H}{8} \times \frac{W}{8} \times 2C$
stage3：Patch Merging -> 6x Swin Transformer Block，输出 $\frac{H}{16} \times \frac{W}{16} \times 4C$
stage4：Patch Merging -> 2x Swin Transformer Block，输出 $\frac{H}{32} \times \frac{W}{32} \times 8C$

4.1 Patch Merging模块

Patch Merging的作用是降维、升通道，例如stage2，先经过Patch Merging，再经过两个Transformer Block结构，已知Transformer输入和输入维度大小不变，即输入Transformer结构的维度是 $\frac{H}{8} \times \frac{W}{8} \times 2C$ ，但是输入Patch Merging的维度是 $\frac{H}{4} \times \frac{W}{4} \times C$ ，说明Patch Merging把输入缩小了一半，维度增加了一倍。

图四 Patch Merging流程图

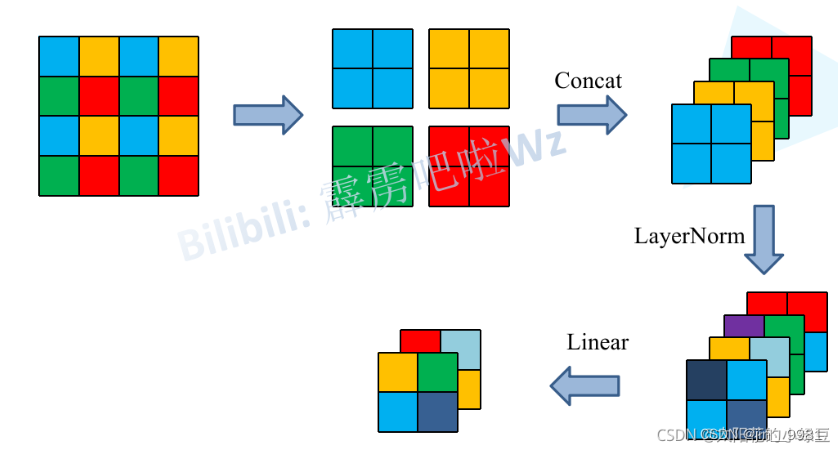
实现流程：
（1）在行方向和列方向上，间隔2选取元素
（2）拼接成张量，通道变成4 * dim
（3）self.reduction：全连接，通道变成2*dim

 def forward(self, x):
    """
    x: B, H*W, C
    """
    H, W = self.input_resolution
    B, L, C = x.shape
    assert L == H * W, "input feature has wrong size"
    assert H % 2 == 0 and W % 2 == 0, f"x size ({H}*{W}) are not even."

    x = x.view(B, H, W, C)

    x0 = x[:, 0::2, 0::2, :]  # B H/2 W/2 C
    x1 = x[:, 1::2, 0::2, :]  # B H/2 W/2 C
    x2 = x[:, 0::2, 1::2, :]  # B H/2 W/2 C
    x3 = x[:, 1::2, 1::2, :]  # B H/2 W/2 C
    x = torch.cat([x0, x1, x2, x3], -1)  # B H/2 W/2 4*C
    x = x.view(B, -1, 4 * C)  # B H/2*W/2 4*C

    x = self.norm(x)
    x = self.reduction(x)

    return x

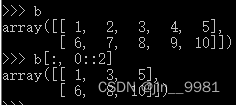
看代码似乎还是不太明白，这里（1）在行方向和列方向上，间隔2选取元素，用了::，没用过这个方法的，可以看下这个例子，间隔n位取数

图五 ::用法

4.2 相对位置编码

Swin Transformer的相对位置编码并不是用在输入部分，而是在Attention计算过程中，QK计算得到attn张量，再加上位置编码。
若特征图按7x7的窗口划分，每个窗口有49个token，他们之间是有一定的位置关系。下面为了方便展示，用2x2大小的图表示。例如2x2的特征图，经过attention的QK计算，变成4x4，那么相对位置编码的大小也是4x4，图六就是相对位置编码。

图六相对位置编码

图六这个编码是怎么得到的？我们一步步详细解释。
（1）绝对位置编码：对于2x2的特征图，它的绝对位置编码是二维的，行和列用0和1表示，如图七。

图七绝对位置

（2）以不同颜色为起点，其他像素的相对位置如图八

图八相对位置

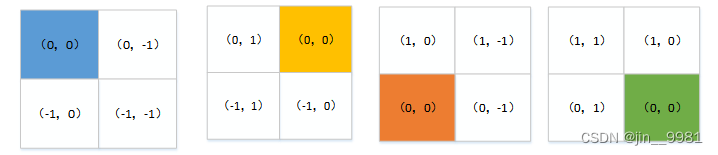
（3）将（2）中的图拉直拼接，得到一个4x4大小的图，如图9

图九拉直拼接

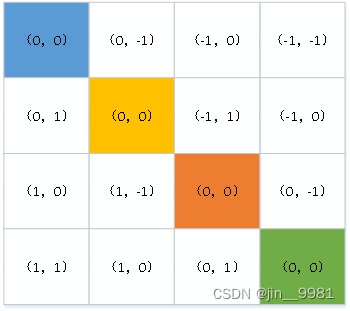
（4）可以发现图9中的数值，既有0、1，也有负数-1，为了使值都大于等于0，行列都加上（M-1），如图十

图十

（5）图十中的位置都是二维，为了得到一维的结果，可以想到的一个方法是将行和列加起来（不同位置数值相同，方法不可取，如图11），另外一个方法是行坐标都乘上2M-1，再和列相加，如图12，得到的结果就跟图六相同。

图11 行列相加

图12

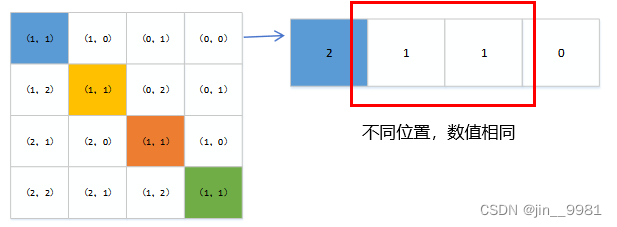
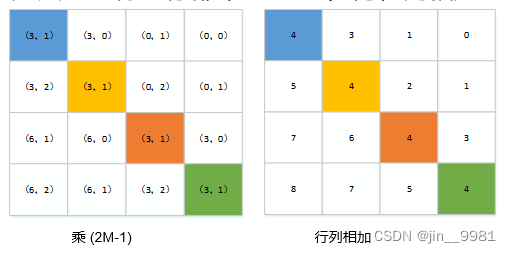
代码实现，可以把代码拷贝到脚本里跑下，跟上面的图做对比：

window_size = [2, 2]
# coords_h、coords_w分别用来代表行列的值，绝对位置
coords_h = torch.arange(window_size[0])
coords_w = torch.arange(window_size[1])   # tensor([0, 1])
coords = torch.stack(torch.meshgrid([coords_h, coords_w])) #torch.Size([2, 2, 2])
coords_flatten = torch.flatten(coords, 1)    # torch.Size([2, 4])
"""
tensor([[0, 0, 1, 1],
        [0, 1, 0, 1]])
"""
relative_coords = coords_flatten[:, :, None] - coords_flatten[:, None, :]  
# torch.Size([2, 4, 4])，得到行列的相对位置
"""
tensor([[[ 0,  0, -1, -1],
         [ 0,  0, -1, -1],
         [ 1,  1,  0,  0],
         [ 1,  1,  0,  0]],

        [[ 0, -1,  0, -1],
         [ 1,  0,  1,  0],
         [ 0, -1,  0, -1],
         [ 1,  0,  1,  0]]])
"""
relative_coords = relative_coords.permute(1, 2, 0).contiguous()  
# torch.Size([4, 4, 2])
relative_coords[:, :, 0] += window_size[0] - 1  # shift to start from 0
relative_coords[:, :, 1] += window_size[1] - 1
relative_coords[:, :, 0] *= 2 * window_size[1] - 1   # 横坐标乘上(2M-1)
relative_position_index = relative_coords.sum(-1)  # 行、列相加
"""
tensor([[4, 3, 1, 0],
        [5, 4, 2, 1],
        [7, 6, 4, 3],
        [8, 7, 5, 4]])
"""

4.3 shifted window

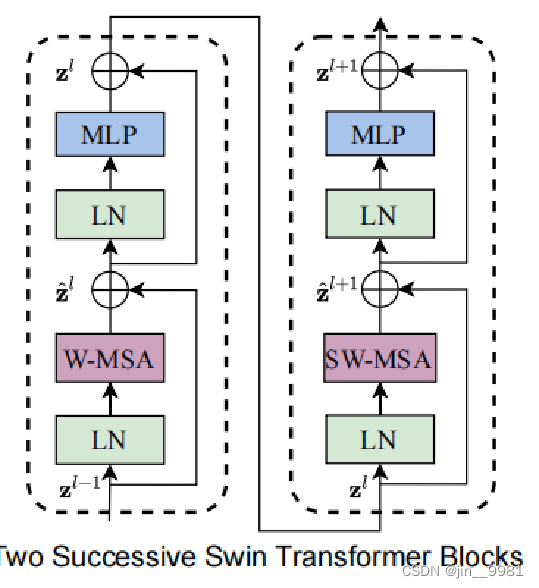
Transformer block用了两种attention，W-MSA（window-multi-head self attention modules，常规attention）和SW-MSA（shifted window-multi-head self attention modules），图13

图13 transformer

假设在原图中，被分为4个窗口，向左向下移位两格，变成9个窗口，图14。

图14 移位窗口

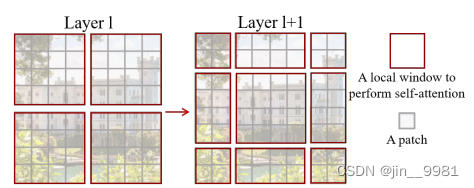
前面提到，attetion只在各个小窗口中计算，那么原本需要4个q、k、v计算的attention，变成了9个q、k、v。在实际代码中，作者通过对特征图移位，并给 Attention 设置 mask 来间接实现的。能在保持原有的 window 个数下，最后的计算结果等价。这是什么意思？我们给九个移位后的窗口用0-8进行编码，如下面图15的左图，再将窗口进行移位，重新拼接成只有四个窗口的图，如右图。
.

图15

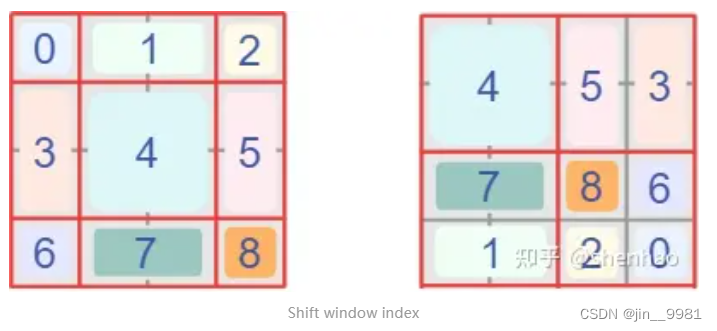
你可能会说，attetion只在小窗口中计算，那例如把窗口5和3拼接成一个窗口，就不能实现窗口attetion了。这里，作者通过设置合理的 mask，让Shifted Window Attention在与Window Attention相同的窗口个数下，达到等价的计算结果，图16，窗口4，拉伸成一维，进行QK计算得到attention向量，而对比5/3窗口，通过QK计算后，其实得到的应该是[5, 53, 5, 53]、[35, 3, 35, 3]、[5, 53, 5, 53]、[35, 3, 35, 3]，但是5窗口attention只计算自己，就mask掉，对应图片灰色格子无数字部分。