---

一、基本概念与原理

1. 假设检验

设总体分布已知，但含有未知参数，对总体的未知参数做出某种假设，在抽取样本及样本观察值的基础上，构造合适的统计量，对假设作出接受与否的判断。

2. 两类错误

（1）第一类错误（弃真）— 若原始假设 $H_0$ 是正确的，但检验结果拒绝 $H_0$ ，称这类错误为第一类错误或弃真。

（2）第二类错误（存伪）— 若原始假设 $H_0$ 是错误的，但检验结果接受 $H_0$ ，称这类错误为第二类错误或存伪。

3. 小概率原理与显著性水平

对假设进行检验的基本思想是采用某种带有概率性质的反证法，这种概率的依据是小概率原理 —— 概率很接近 0 的事件在一次试验或观察中，认为备择假设不会发生。若小概率事件发生了，则拒绝原假设。

小概率事件中的“小概率”的值没有统一规定，通常是根据实际问题的要求，规定一个界限 $\alpha (0<\alpha <1)$ ，当一个事件的概率不大于 $\alpha$ 时，即认为它是小概率事件。在假设检验问题中，$\alpha$ 称为显著性水平，通常取 $\alpha =0.1,0.05,0.01$ 等。

---

二、假设检验的基本步骤

1. 给出未知参数的原始假设 $H_0$ ，及备择假设 $H_1$ ；
2. 选择合适的统计量，当原始假设 $H_0$ 为真时，确定统计量服从的分布；
3. 在显著性水平下，确定原始假设 $H_0$ 的拒绝域；
4. 将样本观察值代入统计量，若统计量的取值不在拒绝域内，则接受 $H_0$ ；否则，拒绝 $H_0$ 。

---

三、一个正态总体均值和方差的假设检验

设总体 $X\sim N(\mu ,{\sigma }^2)$，$(X_1,X_2,\cdots ,X_n)$ 为来自总体 $X$ 的简单随机样本，样本观察值为 $(x_1,x_2,\cdots ,x_n)$ 。

以检验均值 $\mu$ 为例：

（1）若参数 ${\sigma }^2$ 已知

考虑双侧假设检验，则

1. 令 $H_0:\mu ={\mu }_0,H_1:\mu \ne {\mu }_0$ ；
2. 选用统计量 $U=(\overline{X}-{\mu }_0)/(\sigma /\sqrt{n})\sim N(0,1)$ ；
3. 上 $\alpha /2$ 分位点为 $z_{\alpha /2}$ ，则拒绝域为 $(-\infty ,-z_{\alpha /2}]\bigcup [z_{\alpha /2},+\infty )$ ；
4. 代入 $\overline{x}$ 进统计量 $U$ 中，若结果不落在拒绝域中，则接受 $H_0$ ，否则拒绝 $H_0$ 。

考虑右侧假设检验，则

1. 令 $H_0:\mu \le {\mu }_0,H_1:\mu >{\mu }_0$ ；
2. 选用统计量 $U=(\overline{X}-{\mu }_0)/(\sigma /\sqrt{n})\sim N(0,1)$ ；
3. 上 $\alpha$ 分位点为 $z_{\alpha }$ ，则拒绝域为 $[z_{\alpha },+\infty )$ ；
4. 代入 $\overline{x}$ 进统计量 $U$ 中，若结果不落在拒绝域中，则接受 $H_0$ ，否则拒绝 $H_0$ 。

考虑左侧假设检验，则

1. 令 $H_0:\mu \ge {\mu }_0,H_1:\mu <{\mu }_0$ ；
2. 选用统计量 $U=(\overline{X}-{\mu }_0)/(\sigma /\sqrt{n})\sim N(0,1)$ ；
3. 下 $\alpha$ 分位点为 $-z_{\alpha }$ ，则拒绝域为 $(-\infty ,-z_{\alpha }]$ ；
4. 代入 $\overline{x}$ 进统计量 $U$ 中，若结果不落在拒绝域中，则接受 $H_0$ ，否则拒绝 $H_0$ 。

其余情形和置信区间的讨论类似，不再赘述，附上结果。

---

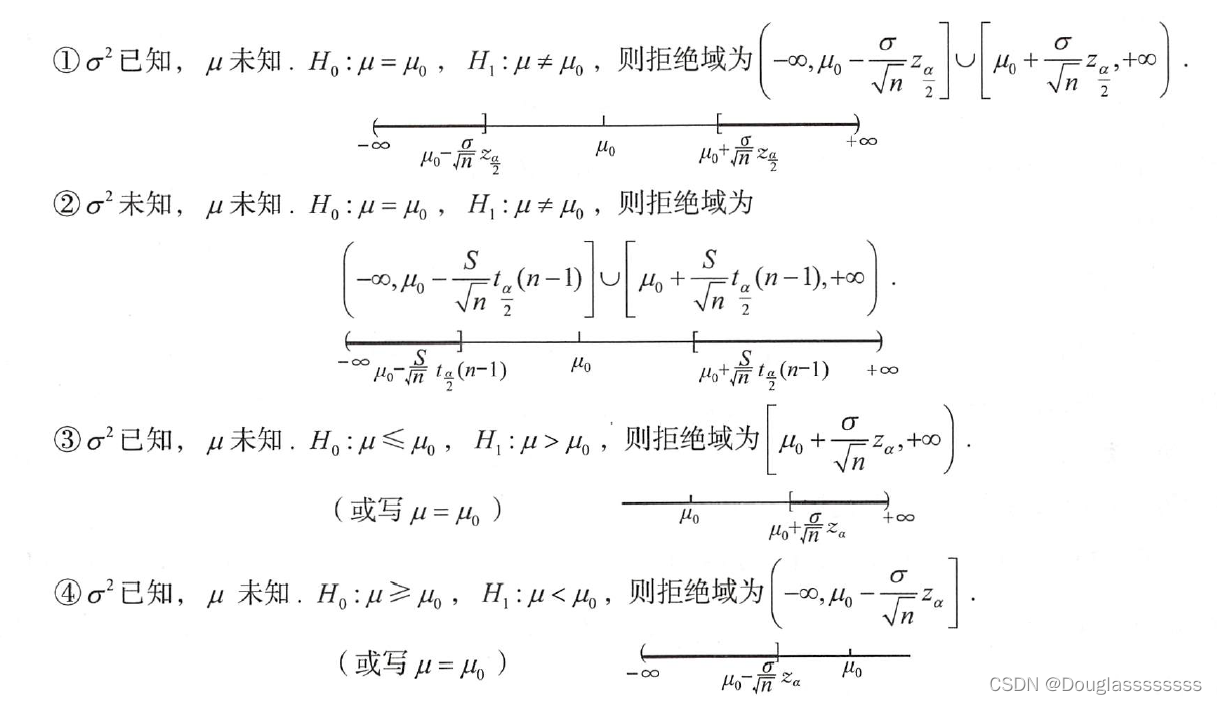
四、两个正态总体的假设检验

---

写在最后

这些内容考前看看就好了，实在是难记。

那到此，全部数学一的理论内容终于终于基本结束了（可能前面还有一些物理、几何应用还没看，后面做到题目补上就是）。只剩下 50 多天的时间了，真的得抓紧。