---

二叉树OJ题

---

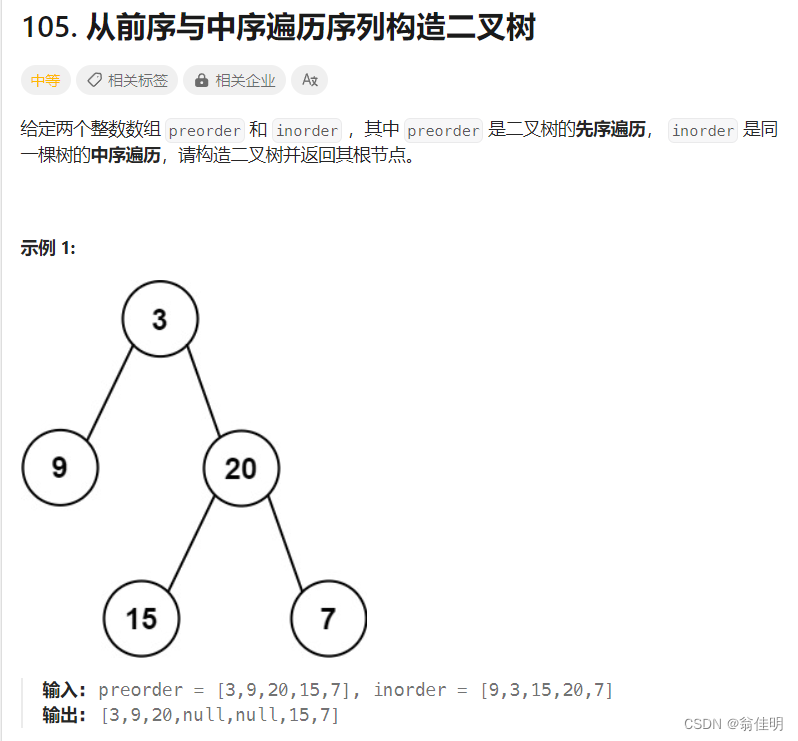
一、用前序和中序遍历构建二叉树

1.思路

1.根据前序遍历找到根结点root

2.在中序遍历中（inBegin=0和inEnd=elem.length-1范围之间）找到根的位置 rootIndex

3.左树就是旧的inBegin=0到新的inEnd=rootIndex-1

4.右树就是新的inBegin= rootIndex+1到旧的inEnd

5.先创建根节点 ，找到当前根结点在中序排列中的位置 ，i++

6.遍历左右子树，返回值由根的左右接收，中序遍历的范围在子树中改变

7.因为右树inBegin = rootindex+1,左树inEnd=rootIndex -1 ，造成inBegin>inEnd时,返回空，说明没有子树了

2.代码

class Solution {
    public int i = 0;
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return buildTreeChild(preorder,inorder,0,inorder.length-1);

    }
    public TreeNode buildTreeChild(int[] preorder, int[] inorder,int inBegin,int inEnd) { 
        if(inBegin>inEnd){
            return null; //没有子树了
        }
        TreeNode root = new TreeNode(preorder[i]);//创建根节点

        //找到当前根结点在中序排列中的位置 
        int rootIndex = findIndex(inorder,inBegin,inEnd,preorder[i]);
        i++;
        root.left = buildTreeChild(preorder,inorder,inBegin,rootIndex-1);
        //遍历创建左右子树，中序遍历中，左右子树的范围改变
        root.right = buildTreeChild(preorder,inorder,rootIndex+1,inEnd);
        
        return root;
        
    }
    private int findIndex(int[] inorder,int inBegin,int inEnd,int key){
        for(int i = inBegin;i<=inEnd;i++){//根基范围找到下标
            if(key == inorder[i]){
                return i;
            }
        }
        return -1;
    }    
}

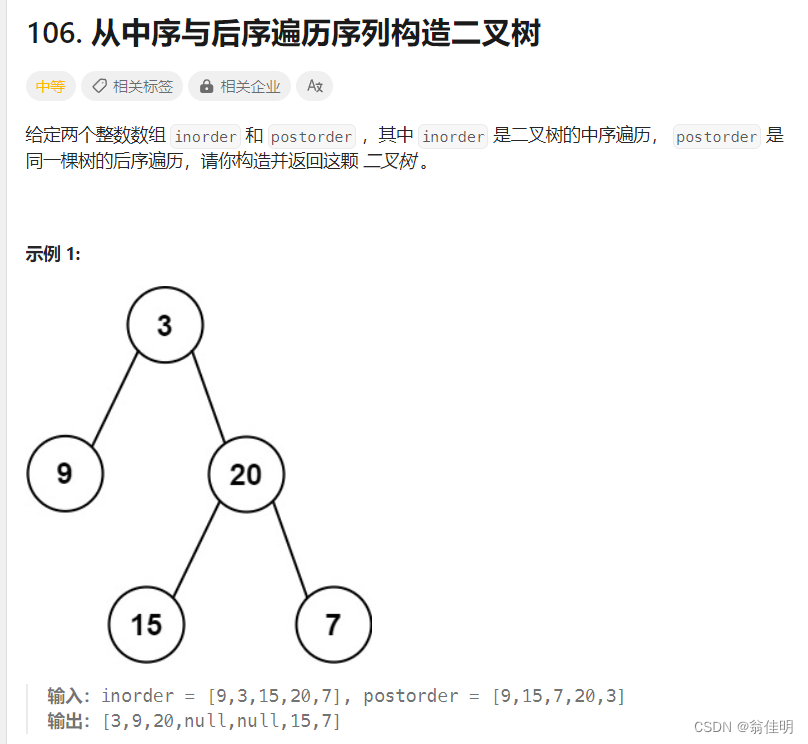
二、用中序和后续遍历构建二叉树

1.思路

1.从后续遍历的末尾找到根节点，i–;

2.在中序遍历中找到根节点的下标

3.后续遍历是 左 -> 右 -> 根，先创建右树，在创建左树

4.右树范围：inBegin = rootIndex+1,左树范围：inEnd = rootindex-1

5.其余原理同上；

2.代码

class Solution {
 public int i = 0;
    public TreeNode buildTree( int[] inorder,int[]postorder) {
        i = postorder.length-1;
        return buildTreeChild(postorder,inorder,0,inorder.length-1);

    }
    public TreeNode buildTreeChild(int[] postorder, int[] inorder,int inBegin,int inEnd) { 
        if(inBegin>inEnd){
            return null; //没有子树了
        }
        TreeNode root = new TreeNode(postorder[i]);//创建根节点

        //找到当前根结点在中序排列中的位置 
        int rootIndex = findIndex(inorder,inBegin,inEnd,postorder[i]);
        i--;

        //遍历创建左右子树，中序遍历中，左右子树的范围改变
    root.right = buildTreeChild(postorder,inorder,rootIndex+1,inEnd);
    root.left = buildTreeChild(postorder,inorder,inBegin,rootIndex-1);       
        return root;
        
    }
    private int findIndex(int[] inorder,int inBegin,int inEnd,int key){
        for(int i = inBegin;i<=inEnd;i++){//根基范围找到下标
            if(key == inorder[i]){
                return i;
            }
        }
        return -1;
    }    
}

点击移步博客主页，欢迎光临~