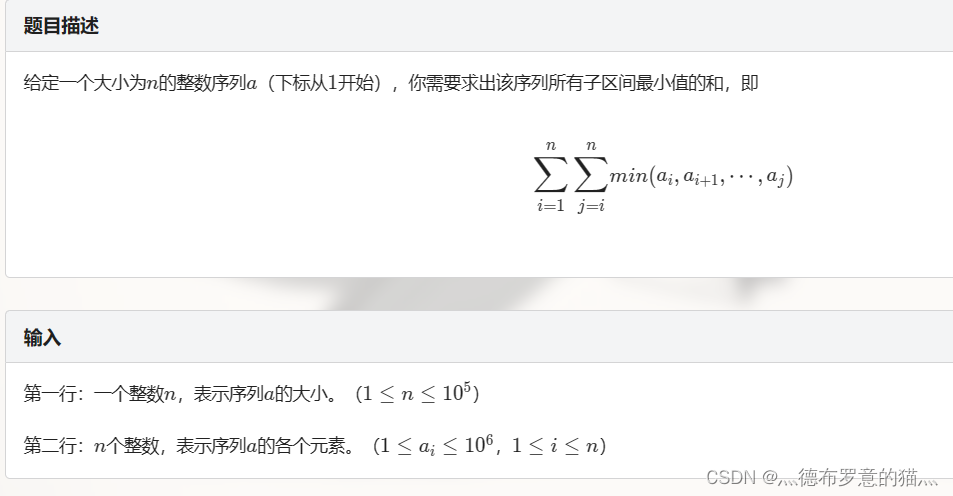
一、预测目标和原始数据展示
(一)预测目标:
通过Economy..GDP.per.Capita.(GDP)和Freedom预测Happiness.Score
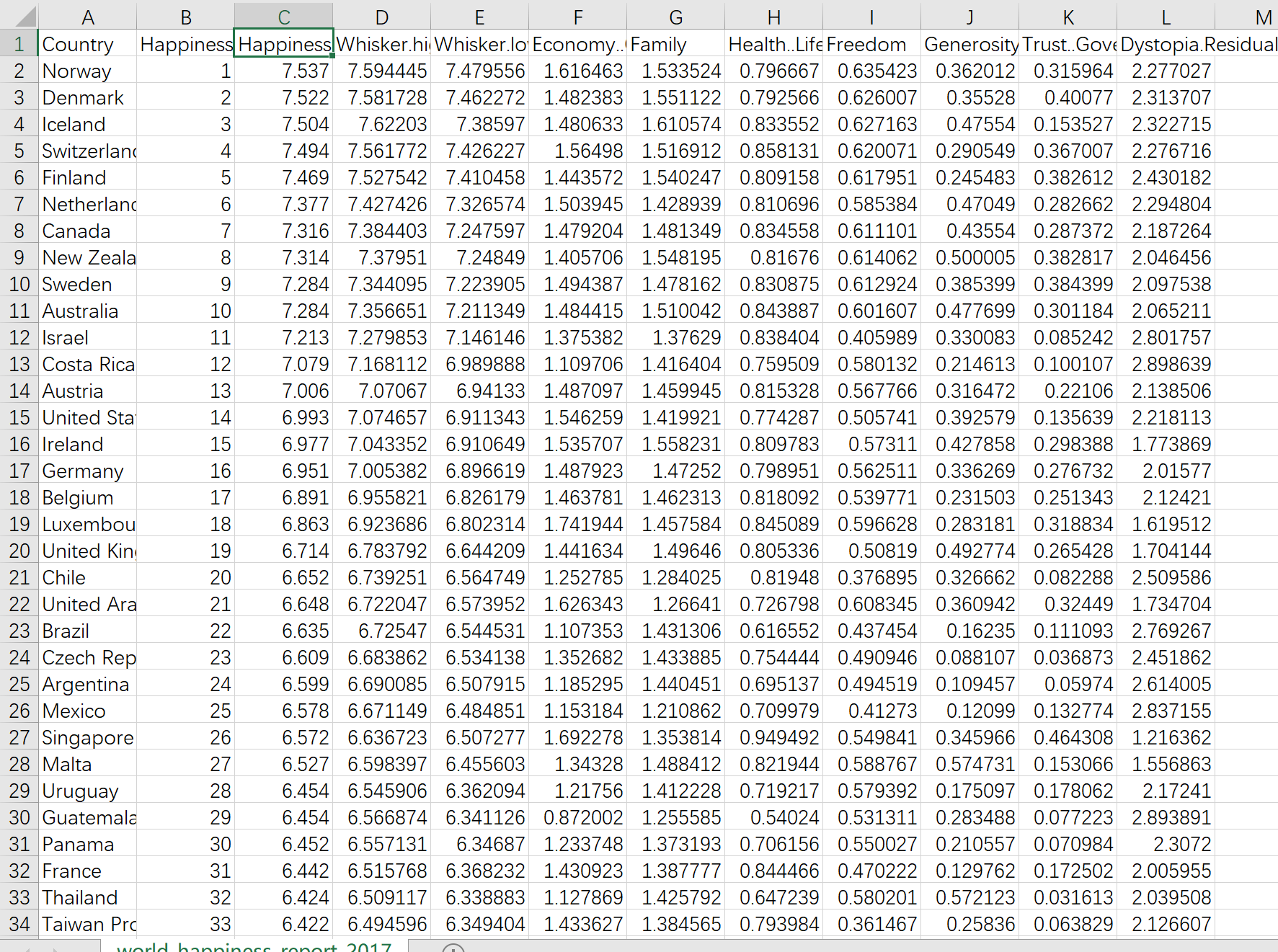
(二)部分数据展示:
特征有很多,本文研究Economy..GDP.per.Capita.(GDP)和Freedom,也就是用Economy..GDP.per.Capita.(GDP)和Freedom预测Happiness.Score。
原始数据链接:
链接:https://pan.baidu.com/s/1yUsHkwGyZafYCvdZu0YHNg?pwd=z6bp
提取码:z6bp
二、数学原理及其应用
(一)所用参数介绍:
Y:我们需要预测的真实值,也就是Happiness.Score(自由指数)
X1:Economy..GDP.per.Capita.(GDP)
X2:Freedom(我理解为一个国家的自由度,调查得到)
θ1:X1的系数
θ2:X2的系数
ε:误差
α:学习率
θ0:偏置项
(二)θ代表什么?
若Y=X1+X2,那么代表着X1、X2对结果Y的影响是相同的,X1取一个数,X2取一个数,那么加起来就是Y。显而易见,GDP+Freedom != Happiness.Score,那么就需要两个数作为X1、X2的系数,来找到θ1和θ2,使得GDP和Freedom对Happiness.Score的影响达到一个最合适的比重,我们的核心目标,就是求得θ1和θ2。
(三)预测公式:

注意这里θX是代表θ1X1+θ2X2,称为预测值。ε是误差。上述公式分开写应该如下:
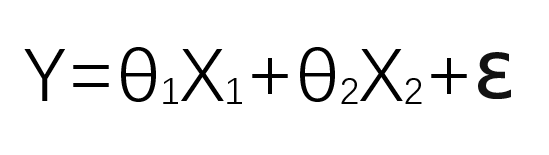
我们希望的是误差越小越好,因为误差越小,我们的预测值就越接近于真实值。
(四)偏置项
在线性回归中,偏置项也被称为截距(intercept),是指模型中的一个常数项,用于调整模型的拟合程度。偏置项通常表示自变量为0时的响应变量值,即直线在y轴上的截距。
偏置项的存在可以使得模型更加灵活,能够更好地拟合数据。如果模型中不包含偏置项,则拟合的直线必须经过原点。
简单理解,就是截距。
(五)前提引入:
1.误差独立并且具有相同的分布,服从均值为0,方差为σ^2的高斯分布。
这个问题我也理解不彻底,只是先作为一个前提条件提出。
2.我们这里所说的X、Y、θ都不单单指一个数,而是一个矩阵,由于运算需要,以上公式需要改动一下,对θ矩阵求转置。
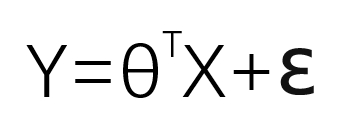
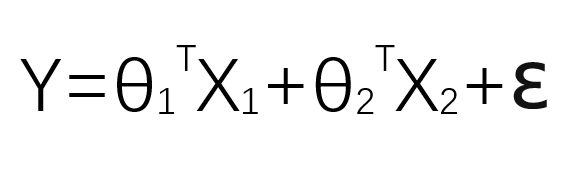
(六)使误差最小:
高斯分布公式:
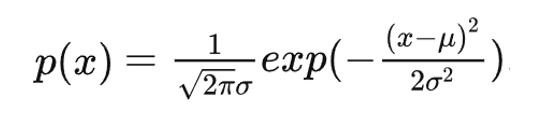
应用到本文中:

我们的目标是希望的是误差越小越好,因为误差越小,我们的预测值就越接近于真实值。
要使误差越小,就要使似然函数越大,在似然函数之前,需先了解最大似然估计:
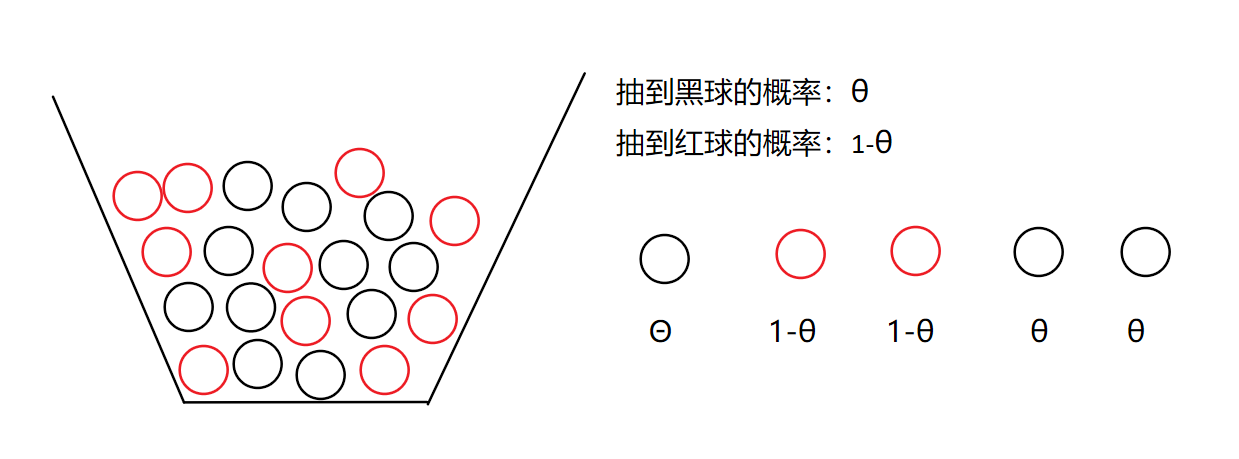
假如一个箱子里有很多很多红球和黑球,数量足够庞大,就假设有70亿个,我任意抽五个球,设抽到黑球的概率为θ,那么抽到红球的概率为1-θ
可以得到似然函数:
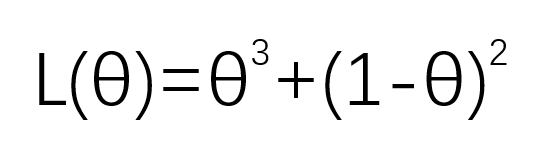
现在抽到的这三黑两红,就是一组观测数据,我要用这组数据,去估计箱子里红球和黑球各有多少,那么我就要使这组数据出现的概率最大,简单来说,如果某个参数值能够使得观测数据出现的概率更大,那么这个参数更有可能是其实际的参数。因为我就抽了这五个,那我应该希望这组观测数据出现的概率更大,才能估计箱子里红球和黑球各有多少。
而似然函数就可以衡量参数与观测数据的匹配程度,所以说要使似然函数越大越好。
这里就是数学问题了,我现在想要在似然函数最大的情况下求得θ,那就对θ求导并使其函数只等于0,因为导数反应的是函数的变化率,或者说是切线斜率,当函数到达最高点时,函数的变化率或者说是切线斜率就等于0,想想一个开口向下的抛物线函数。在独立同分布的条件下,联合概率密度等于边缘概率密度的乘积。

回到线性回归中。
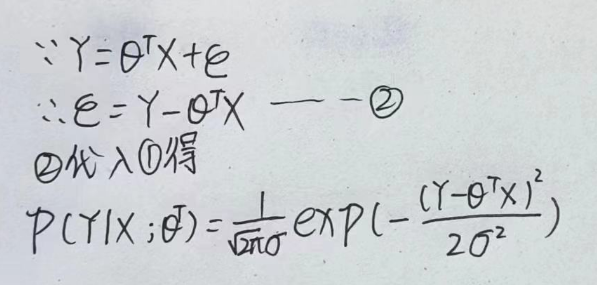
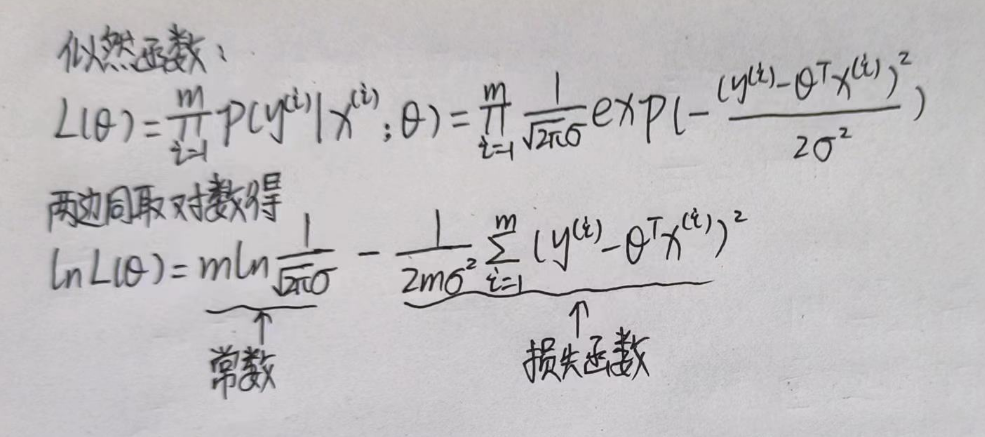
现在,得到了一个常数和一个函数,我们称他为损失函数,要使似然函数最大,那么问题进一步转化为了让损失函数最小。我们把损失函数定义出来,如下:

想要解决时损失函数最小的问题,需要用到梯度下降算法,但在这之前,其原理需要用到高数中的方向导数与梯度。
(七)方向导数与梯度
高数书中这么引入方向导数:偏导数反映的是函数沿坐标轴方向的变化率,但许多物理现象告诉我们,只考虑沿坐标轴方向的变化率是不够的,例如:热空气要向冷的地方流动,气象学中就要确定大气温度,气压沿着某些方向的变化率,因此,我们有必要来讨论函数沿任一指定方向的变化率问题。
梯度下降算法得到loss函数的最小值,而下降不能胡乱下降,需要找到一个方向,也就是函数沿任一指定方向的变化率,以下来证明沿哪个方向下降:
这是一个常见的高数题,请先记住题中的梯度向量:
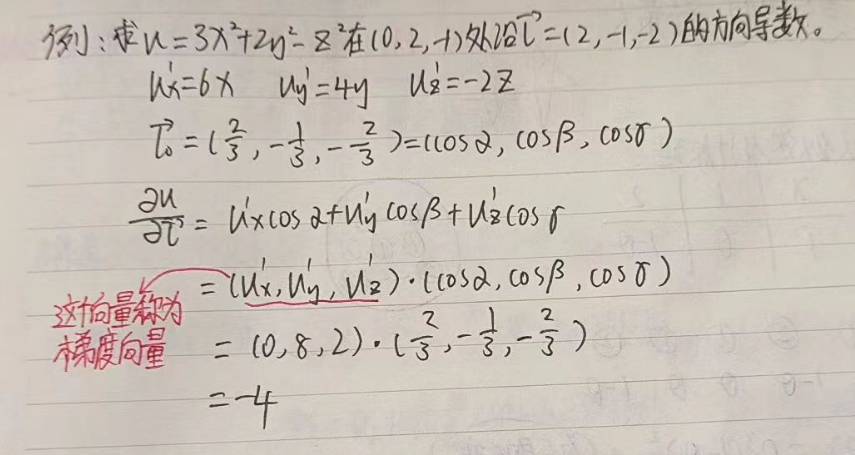
梯度量永远指向方向导数变化最大的向,换句话说,梯度向量的方向是函数上升最快的方向。

那么现在,进入梯度下降算法。
(八)梯度下降
梯度下降算法的基本思路是通过不断迭代来更新模型参数,直到达到最小化目标函数的效果。具体地,给定一个初始点,我们计算当前点的负梯度(即梯度的相反数),并沿着负梯度的方向更新参数。重复这个过程,直到收敛到一个局部极小值或全局极小值。 在梯度下降算法中,学习率是一个非常关键的参数。它决定了每一次迭代中,更新参数的幅度大小。这个学习率,可以理解为步长。
本文研究两个特征值,Economy..GDP.per.Capita.(GDP)和Freedom,对应的损失函数定义和更新参数θ如下:
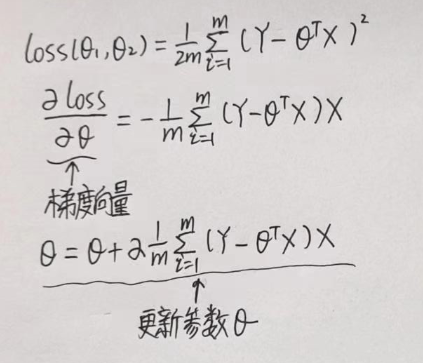
梯度量永远指向方向导数变化最大的向,换句话说,梯度向量的方向是函数上升最快的方向。所以说虽然求导后得负,但要取反。上述更新参数的算法为批量梯度下降。
以上就为我理解的原理,下面进入代码模块
三、代码模块
(一)数据预处理
#Preprocess_data.py
import numpy as np
import pandas as pd
def Preprocess_data(train_X1):
Mean_value = np.mean(train_X1,0) #求得均值
Standard_deviation = np.std(train_X1,0) #求得标准差
train_X1 = (train_X1 - Mean_value)/Standard_deviation
sample_number = train_X1.shape[0]
train_X1 = np.hstack((np.ones((sample_number, 1)), train_X1))
return train_X1为什么要对数据进行预处理?
如果两种数据相差太大,那么会对预测结果造成非常大的误差,假如说要用年龄和身高作为预测数据的话,例如:年龄:[20,21,10,18,27,33,60......],身高:[180,170,175,169,166,185,187......],两位数和三位数的相差太大了,那么求得的他们的系数θ也会相差很大,造成的是身高对预测结果的影响远远大于年龄对预测结果的影响,这样的误差对模型十分致命,所以,我们要对数据进行预处理。
归一化预处理:
通过将每个特征的值减去均值,并除以标准差,实现了对特征值的归一化。这样做可以使得各个特征的取值范围相对统一,避免某些特征因为数值范围过大而在优化过程中权重变化较小或者被主导的问题。参考概率论中的随机变量标准化正态分布。
train_X1 = np.hstack((np.ones((sample_number, 1)), train_X1))
在二(四)中我们提到偏置项,为数据添加一列1,就是为了得到偏置项,也就是截距。
(二)梯度下降算法实现
#Linear_Regression.py
import numpy as np
from Preprocess_data import Preprocess_data
class LinearRegression:
def __init__(self,train_X1,train_Y):
train_X1 = Preprocess_data(train_X1)
self.train_X1 = train_X1
self.train_Y = train_Y
self.theta = np.zeros(((self.train_X1.shape[1]),1))
def train(self,alpha,train_times):
record_loss = self.gradient_descent(alpha,train_times)
return self.theta,record_loss
def gradient_descent(self,alpha,train_times):
record_loss = []
for _ in range(train_times):
self.gradient_step(alpha)
record_loss.append(self.compute_loss(self.train_X1,self.train_Y))
return record_loss
def gradient_step(self,alpha):
prediction = LinearRegression.hypothesis(self.train_X1,self.theta)
delta = prediction - self.train_Y
theta = self.theta
Sample_number = self.train_X1.shape[0]
theta = theta - alpha*(1/Sample_number)*(np.dot(delta.T,self.train_X1)).T
self.theta = theta
@staticmethod
def hypothesis(train_X1,theta):
prediction = np.dot(train_X1,theta)
return prediction
def compute_loss(self,train_X1,train_Y):
sample_number = train_X1.shape[0]
delta = LinearRegression.hypothesis(self.train_X1,self.theta)- train_Y
loss = (1/2)*np.dot(delta.T,delta)/sample_number #使用均方误差来衡量线性回归模型的拟合程度
return loss[0][0]
def predict(self,X1_predictions):
X1_predictions = Preprocess_data(X1_predictions)
final_prediction = LinearRegression.hypothesis(X1_predictions,self.theta)
return final_predictionself.theta = np.zeros(((self.train_X1.shape[1]),1))
数据预处理中我们为了得到偏置项为数据添加了一列1,由于矩阵相乘的特点同时也是为了得到偏置项,我们按照数据的列数,创建theta的行数。
theta = theta - alpha*(1/Sample_number)*(np.dot(delta.T,self.train_X1)).T
这一步就是二(八)中批量梯度下降数学表达式的实现。
@staticmethod
通过将方法定义为静态方法,可以直接通过类名调用该方法,而不需要先创建类的实例。这在某些情况下可以简化代码的编写和调用方式。
(三)数据传入和模型
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import plotly.express as px
import plotly.graph_objects as go
from Linear_Regression import LinearRegression
data = pd.read_csv('D:\\Programming\\MicrosoftVSCodeData\\MachineLearning\\data\\world-happiness-report-2017.csv')
train_data = data.sample(frac=0.8)
test_data = data.drop(train_data.index)
X1_title = "Economy..GDP.per.Capita."
X2_title = "Freedom"
Y_title = "Happiness.Score"
X_train = train_data[[X1_title, X2_title]].values
Y_train = train_data[[Y_title]].values
test_X = test_data[[X1_title, X2_title]].values
test_Y = test_data[[Y_title]].values
X = data[[X1_title, X2_title]]
y = data[Y_title]
train_times = 500
alpha = 0.01
mesh_size = .02
margin = 0
# Condition the model on sepal width and length, predict the petal width
model = LinearRegression(X_train,Y_train)
(theta, loss_history) = model.train(alpha,train_times)
print('开始损失',loss_history[0])
print('结束损失',loss_history[-1])
plt.plot(range(train_times), loss_history)
plt.title('loss_function')
plt.show()
# Create a mesh grid on which we will run our model
x_min, x_max = X[X1_title].min() - margin, X[X1_title].max() + margin
y_min, y_max = X[X2_title].min() - margin, X[X2_title].max() + margin
xrange = np.arange(x_min, x_max, mesh_size)
yrange = np.arange(y_min, y_max, mesh_size)
xx, yy = np.meshgrid(xrange, yrange)
# Condition the model on sepal width and length, predict the petal width
pred = model.predict(np.c_[xx.ravel(), yy.ravel()])
pred = pred.reshape(xx.shape)
# Generate the plot
fig = px.scatter_3d(train_data, x=X1_title, y=X2_title, z=Y_title)
fig.update_traces(marker=dict(size=10))
fig.add_trace(go.Surface(x=xrange, y=yrange, z=pred, name='Predict_Happiness'))
fig.add_trace(go.Scatter3d(
x=test_data[X1_title],
y=test_data[X2_title],
z=test_data[Y_title],
mode='markers',
marker=dict(
size=10,
color='red'
),
name='test_data'
))
fig.show()
真没找到合适的多特征线性回归模型,不得已出此下策用非线性的模型改成线性,原模型如下:
模型来源:Ml regression in Python (plotly.com)
将模型代码copy,数据改成自己的数据即可。如果网站加载缓慢的,用UU加速器,搜索学术资源进行加速(没有打广告)。
模型改动:添加了以下代码把测试数据加入图中进行对比和画出损失函数图像。
fig.add_trace(go.Scatter3d(
x=test_data[X1_title],
y=test_data[X2_title],
z=test_data[Y_title],
mode='markers',
marker=dict(
size=10,
color='red'
),
name='test_data'
))
print('——————————————————————————')
print('开始损失',loss_history[0])
print('结束损失',loss_history[-1])
plt.plot(range(train_times), loss_history)
plt.title('loss_function')
plt.show()四、程序调试和模型展示
经数据代入方程计算得出误差大约在0.4左右,如果把剩余的6个特征也加入方程,误差可更小。


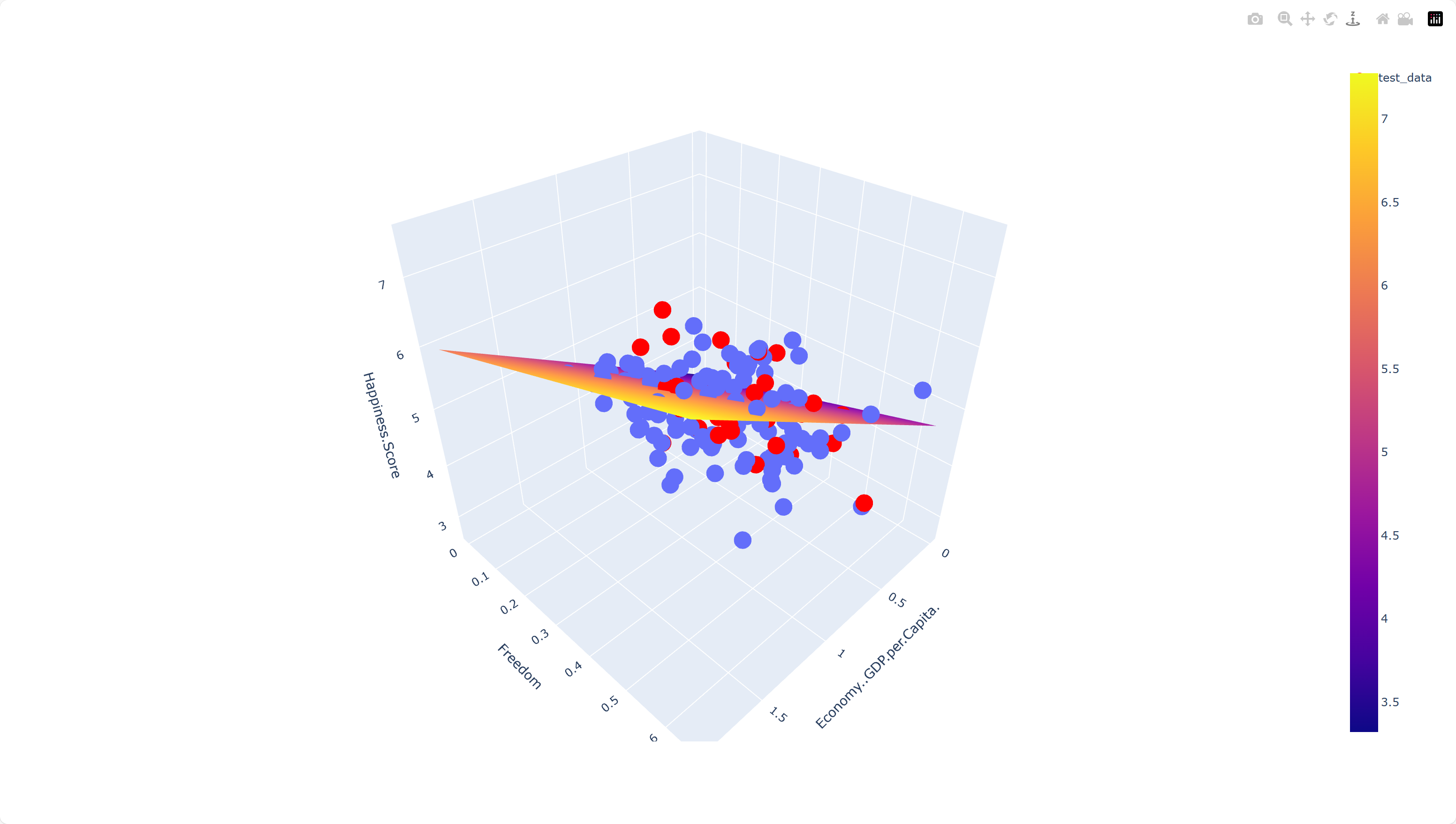
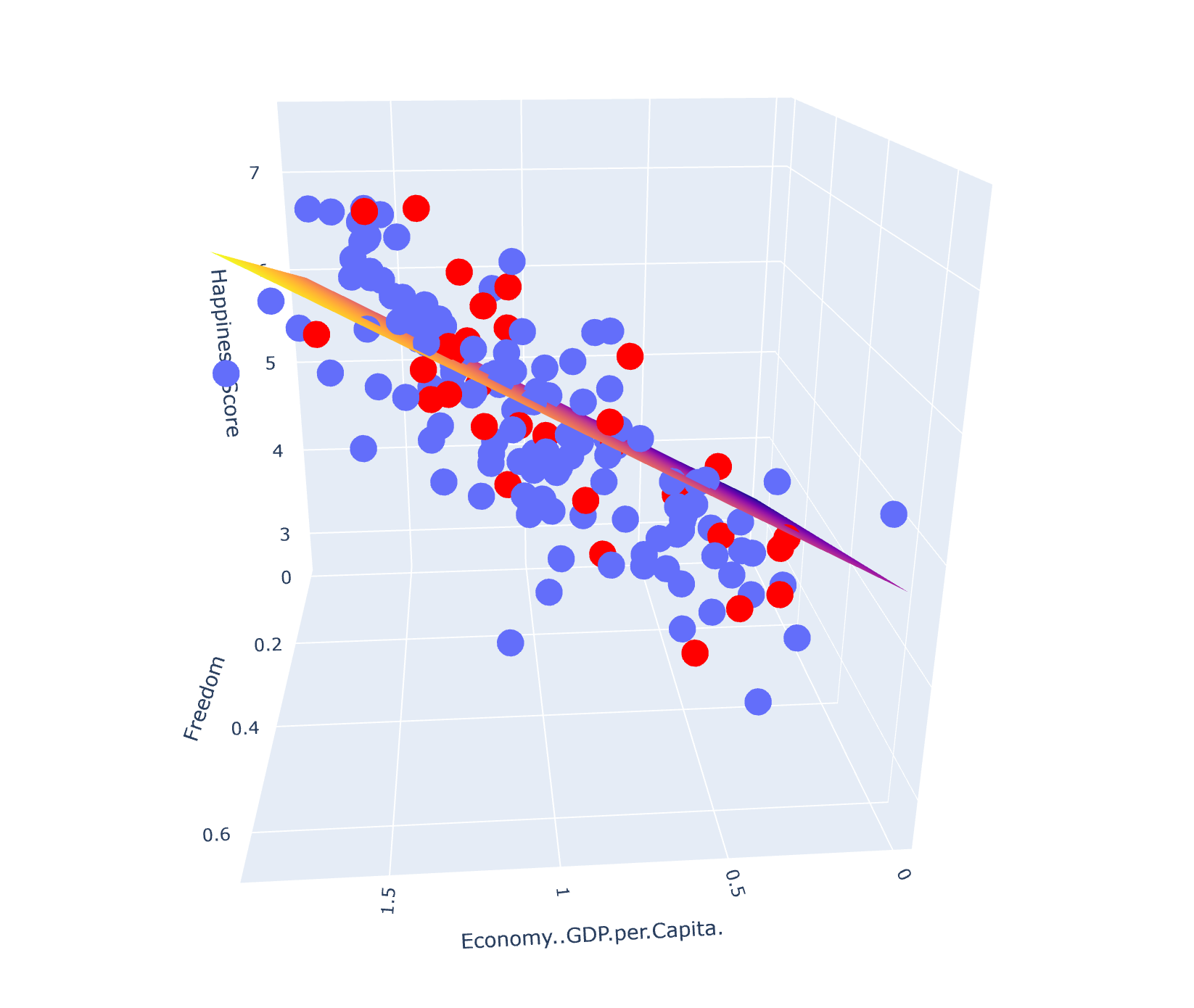
五、参考课程和鸣谢
【多元微分专题】第六期:方向导数和梯度的直观理解_哔哩哔哩_bilibili
9-多特征回归模型_哔哩哔哩_bilibili
高斯分布 - 知乎 (zhihu.com)
【梯度下降】3D可视化讲解通俗易懂_哔哩哔哩_bilibili
每天一个数学小知识——导数的定义_哔哩哔哩_bilibili
有些参考文章可能未列出,感谢各位老师的教导!
本人学术不精,如有错误望指正,感谢!