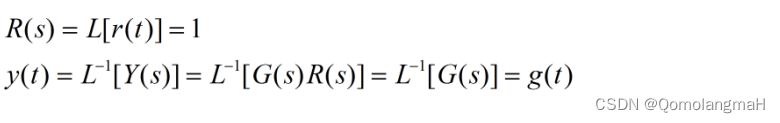第2章 数学模型

基本概念

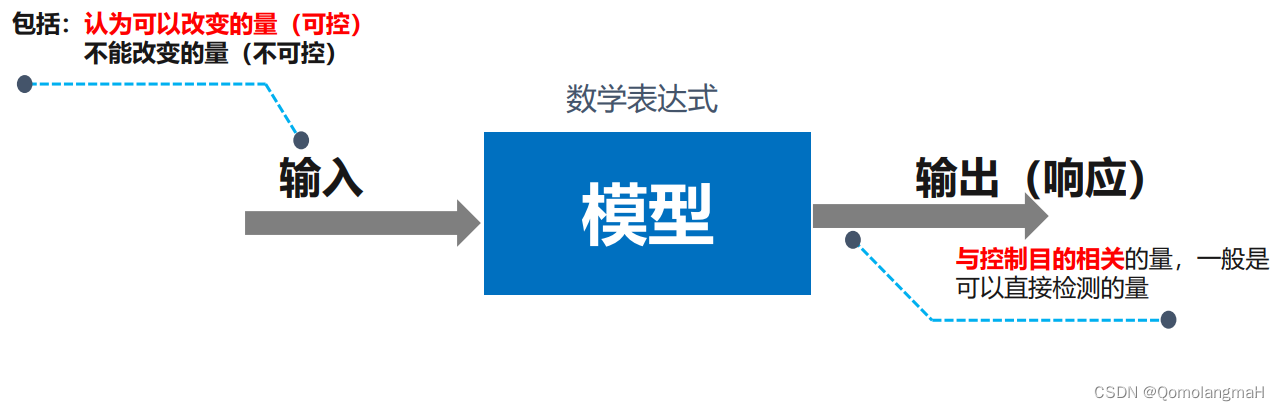
• 系统的数学模型，是描述系统输入、输出量以及内部各变量之间关系的数学表达式，它揭示了系统结构及其参数与其性能之间的内在关系。
  

• 系统数学模型有多种形式,这取决于变量和坐标系统的选择：

  • 在时间域,通常采用**微分方程或一阶微分方程组(状态方程)**的形式;
  • 在复数域则采用传递函数形式;
  • 而在频率域采用频率特性形式。

2.1 控制系统的运动微分方程

• a. 常微分方程的一般标准形式

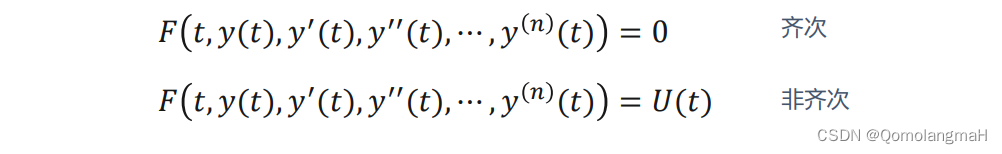
• 微分方程的阶次——n

• 微分方程的解——**函数 **

• 微分方程的通解——包含任意n个常数的解

• 微分方程的特解

• b. 线性定常系统微分方程的一般标准形式

  • 什么是线性? ->满足叠加原理
  • 什么是定常 (时不变) ?
  • 什么是阶次?

  线性定常系统微分方程的一般形式：
  

2.1.1 建立数学模型的一般步骤

• 确定系统输入、输出
• 根据物理定律建立方程组
• 消去中间变量
• 画成标准形式

2.1.2 控制系统微分方程的列写

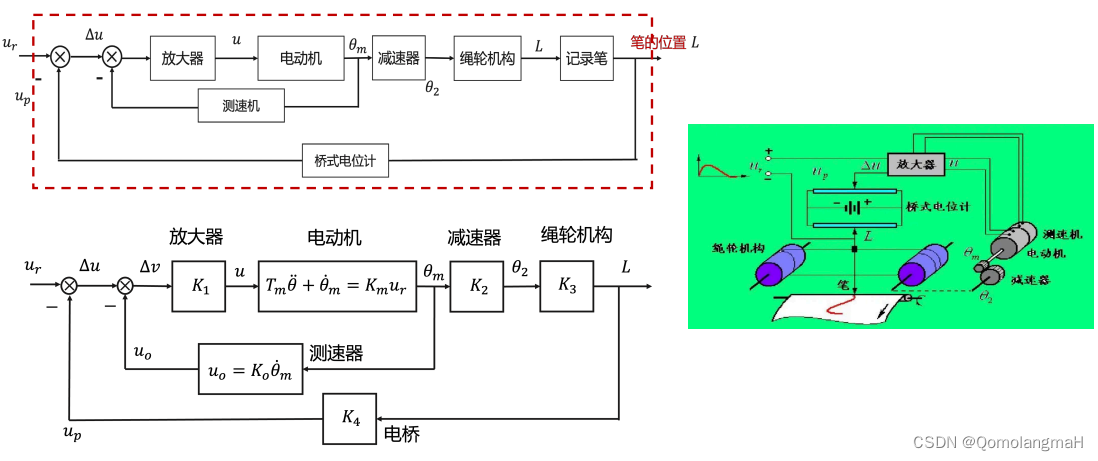
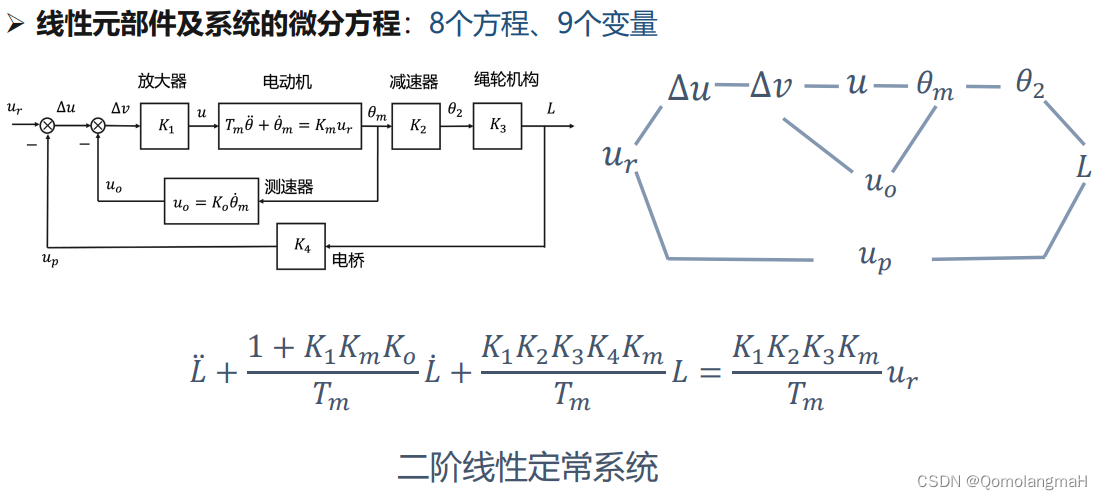
2.2 拉氏变换和反变换

2.2.1 拉氏变换的定义

2.2.2 典型函数的拉氏变换

拉氏变换是一种线性变换，将变量从时间域变换到复数域，将微分方程变换为s 域中的代数方程来处理。

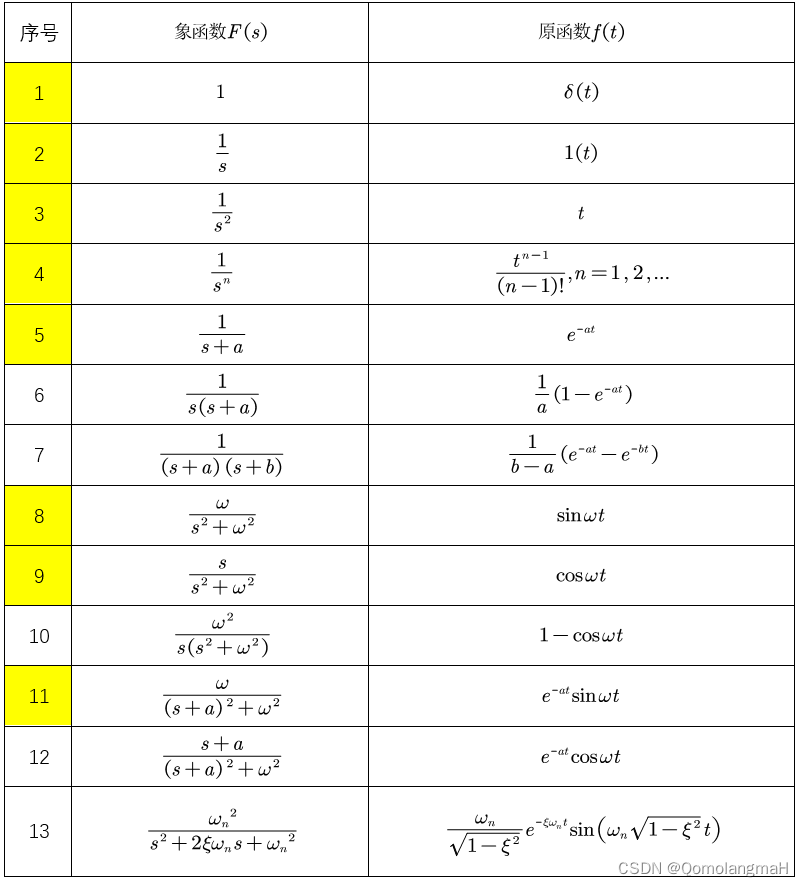
图源

2.2.3 拉氏变换的主要定理

2.2.4 拉氏反变换

P 24

2.2.5 应用拉氏变换求解线性微分方程

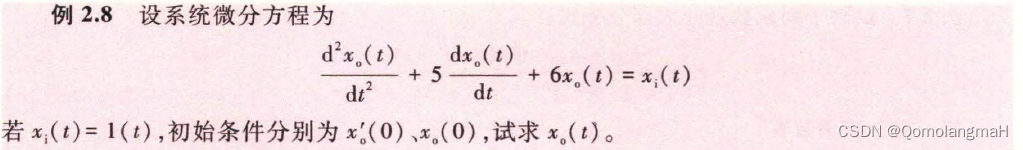
2.3 传递函数

2.3.1 传递函数的概念和定义

​ 对于线性定常系统，在零初始条件下，系统输出量的拉氏变换与引起该输出的输入量的拉氏变换之比，称为系统的传递函数。

2.3.2 特征方程、零点和极点、（零点、极点分布图）

2.3.3 关于传递函数的几点说明

• 传递函数的概念只适用于** 线性定常系统!!!，它是在 零初始条件!!!**下定义的

• 传递函数是复变量s的有理分式函数，即: n>=m 各系数均为实数

• 传递函数是系统的数学描述。物理性质不同的系统可以具有相同的传递函数(相似系统)

• 在同一系统中，当取不同的物理量作输入或输出时，其传递函数也可以不同

• 传递函数是由相应的零、极点组成—与s平面零极点图对应

• 传递函数表示线性定常系统传递、变换输入信号的能力，全面反应系统本身的性能，只与系统或元件的结构和参数有关，与输入量的形式 (幅度、大小) 无关

• 传递函数的拉氏反变换是系统的脉冲响应 !!!*

  • 

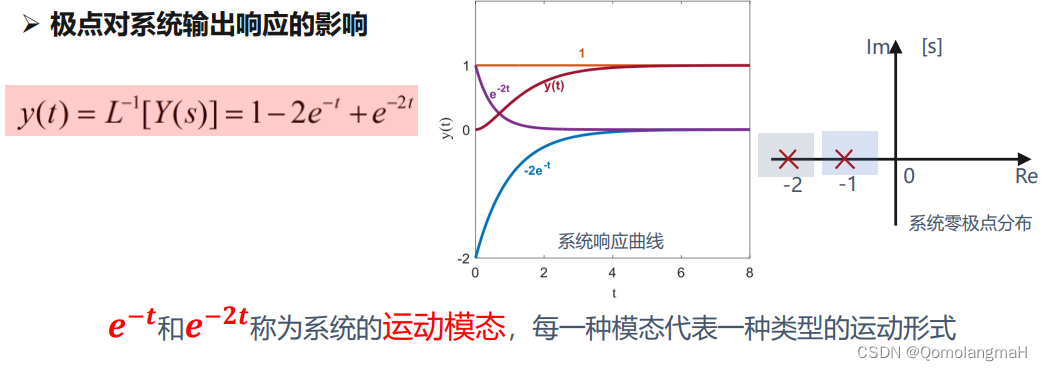
• 极点的作用

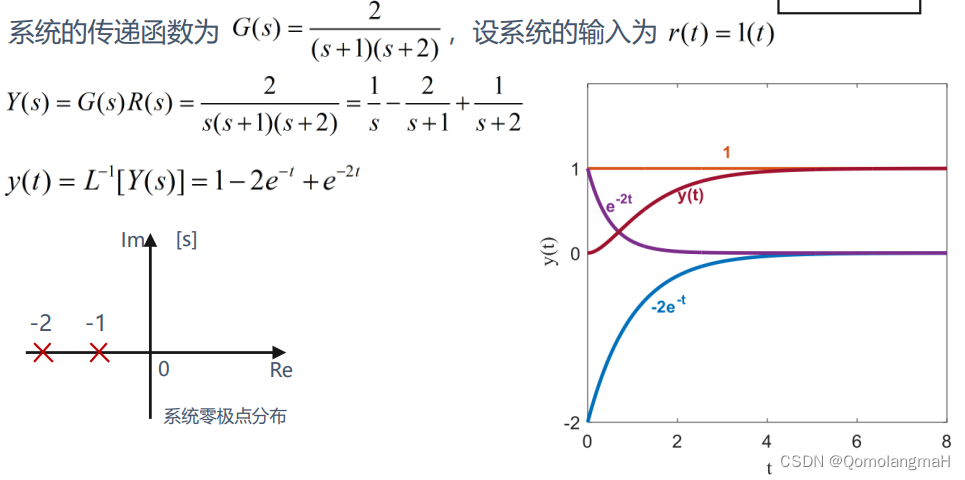
• 极点对系统输出响应的影响

  • 系统自由运动模态由G(s)的极点决定，极点性质不同，其运动模态也不同

    • 

  • 自由运动过程中，靠复平面虚轴最近的极点所对应的自由运动模态所占比重 最大，且衰减也是最慢 的，动态响应过程的大部分由该极点决定。

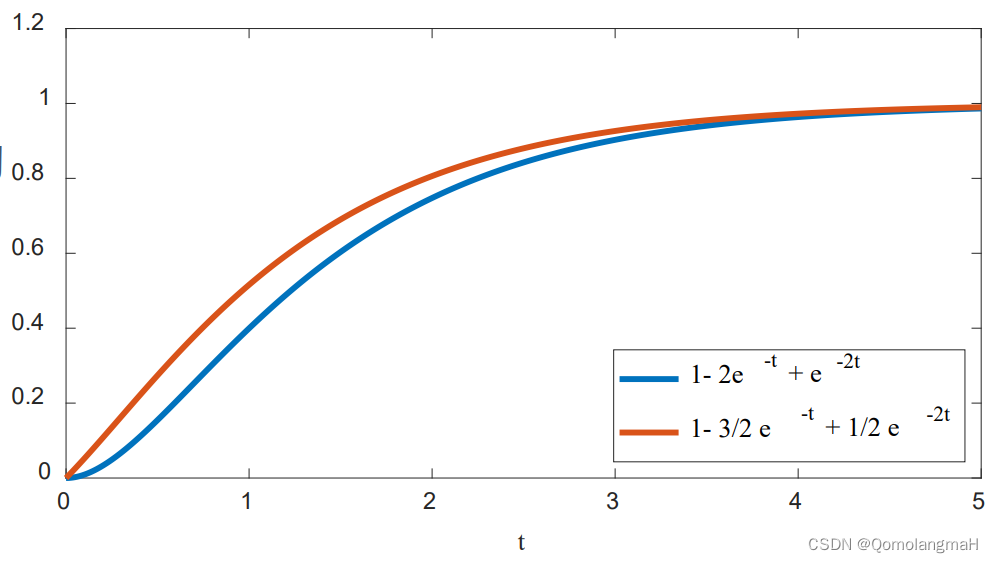
• 零点对系统输出的影响

  • 

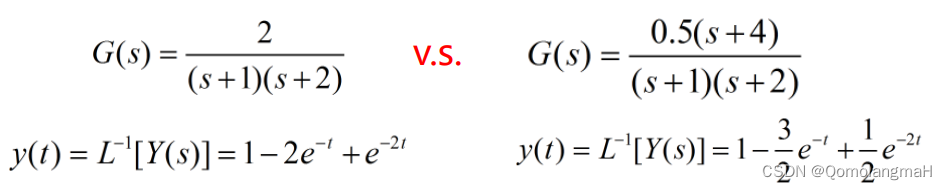
  • 零点不能形成运动模态

  • 系统零点可以影响各个运动模态在响应中的比重

    • 

2.3.4 典型环节及其传递函数

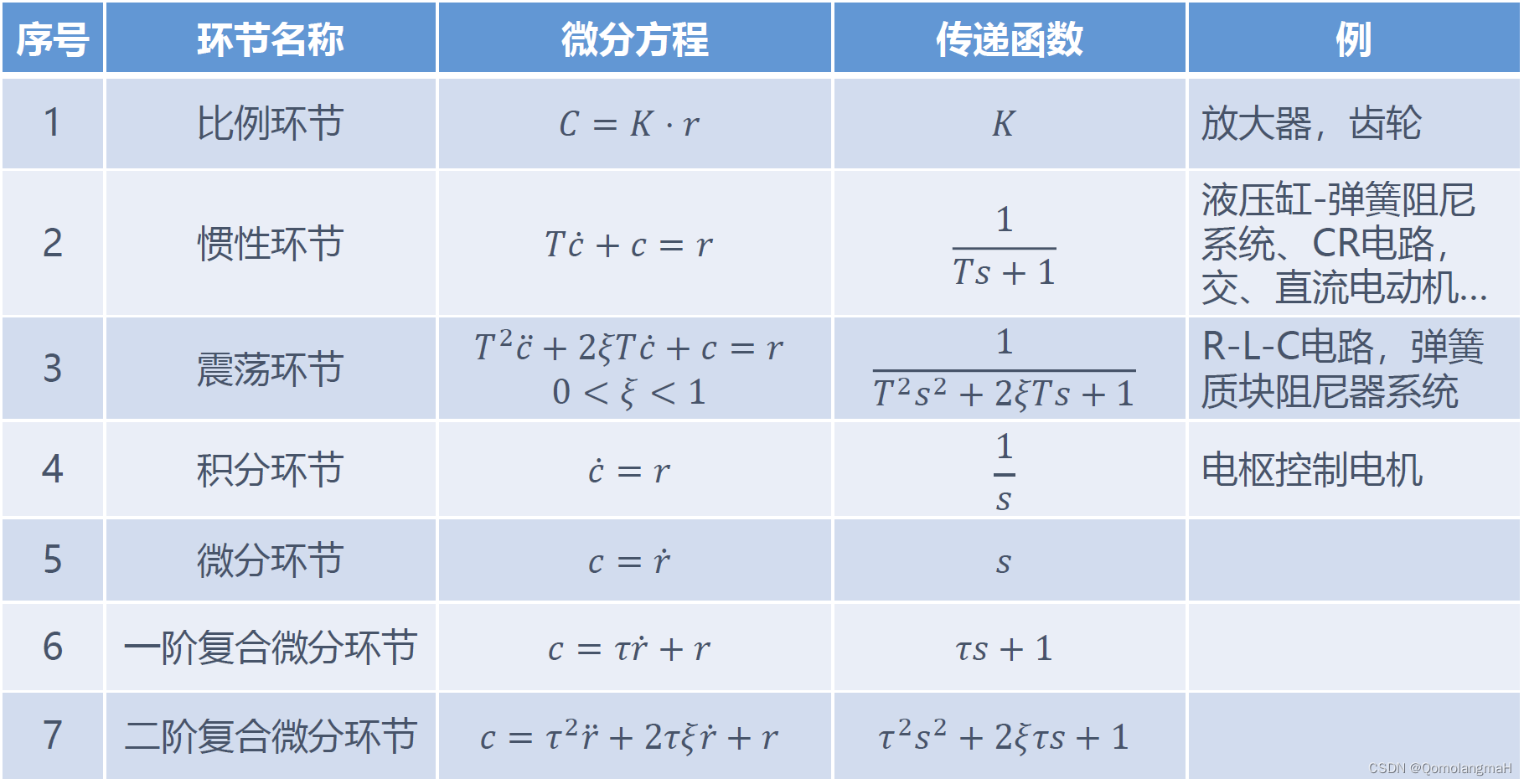
2.3.5 根据系统运动的微分方程模型求传递函数